Skip to main content

1.4 Finite Automata

1.4.1 Concepts​

定义：有限状态机（FA）是一个包含有限个元素（作为 “状态节点”），以及元素间转移的有向边的 图数据结构。

特征：有限自动机有一个有限状态集合和一些从一个状态通向另一个状态的边，每条边上标记有一个符号；其中一个状态是初态，某些状态是终态。

其中，确定有限自动机（Deterministic Finite Automata，DFA）是有限自动机的特殊情况，它不会有从同一状态出发的、两条或以上标记为同样符号的 边，这种有限自动机称为 “确定有限自动机”，意为：“根据输入情况和当前状态一定能确定下一状态” 的有限自动机。

相反地，有不确定有限自动机（Nondeterministic Finite Automata，NFA）；

运行逻辑：从初始状态出发，对于输入字符串中的每个字符，自动机都将沿着一条确定的边到达另一状态，这条边必须是标有输入字符的边。

对 ｎ个字符的字符串进行了ｎ次状态转换后，如果自动机到达了终态，自动机将接收该字符串。若到达的不是终态，或者找不到与输人字符相匹配的边，那么自动机将拒绝接收这个字符串。

对于 NFA，针对同一个输入可以对应多个状态（同时位于多个状态），在输入结束后，只要存在一个状态位于终态，那么就会接受这个输入。

根据自动机的运行逻辑，我们可以将一个正则表达式转换为一个 DFA / NFA，以此实现正则表达式的行为。

如果转换为 NFA，则虽然转换过程简单，但运行过程可能出现状态爆炸的问题；

1.4.2 Regular Expression to NFA​

可以按照下面的算法将 RE 转换为一个有头有尾的 NFA；其中 “头” 为末端状态，“尾” 为开始边。

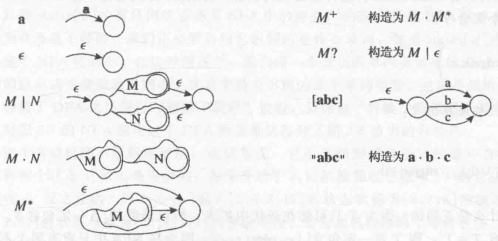
思考：M ∣ NM\space|\space N 表示中的两个 ε\varepsilon 和最后一个状态是否必要？

答案是，如果表达式只有 M ∣ NM\space|\space N 的话，是不必要的。但是为了将一段表达式看作一个有一个头、一个尾的整体，可以等价的加上去（这样方便了像 (M∣N)⋅A(M|N)\cdot A 一样的表达式的转换）；

1.4.3 NFA to DFA​

转换算法的主要规则如下：

  • 实际上转换的过程就是模拟 NFA 的过程，DFA 中每个状态都是 NFA 状态节点的非空真子集；
  • 创建 DFA start state：从 NFA 入口通过 ε\varepsilon-move 能到达的所有状态的集合；
  • 创建转换过程（transition）S→aS′S\rightarrow^a S^\prime：其中 aa 为 NFA 中对应 状态 S 通过一个 aa-move 和若干个 ε\varepsilon-move 所能到达的所有状态的集合；

值得注意的是，转换的时候可能存在优先级关系，因此引入 Priority Rule：

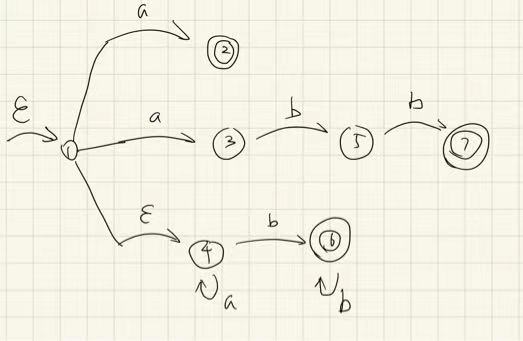
假设正则表达式为 a ∣ abb ∣ a∗b+a\space|\space abb\space|\space a^{*}b^{+}，那么 NFA 为：

注意到优先级应该是 2 优于 7 优于 6（根据在正则式中的先后顺序）；

只要我们再加入下面的转换技巧，就能保证优先级：

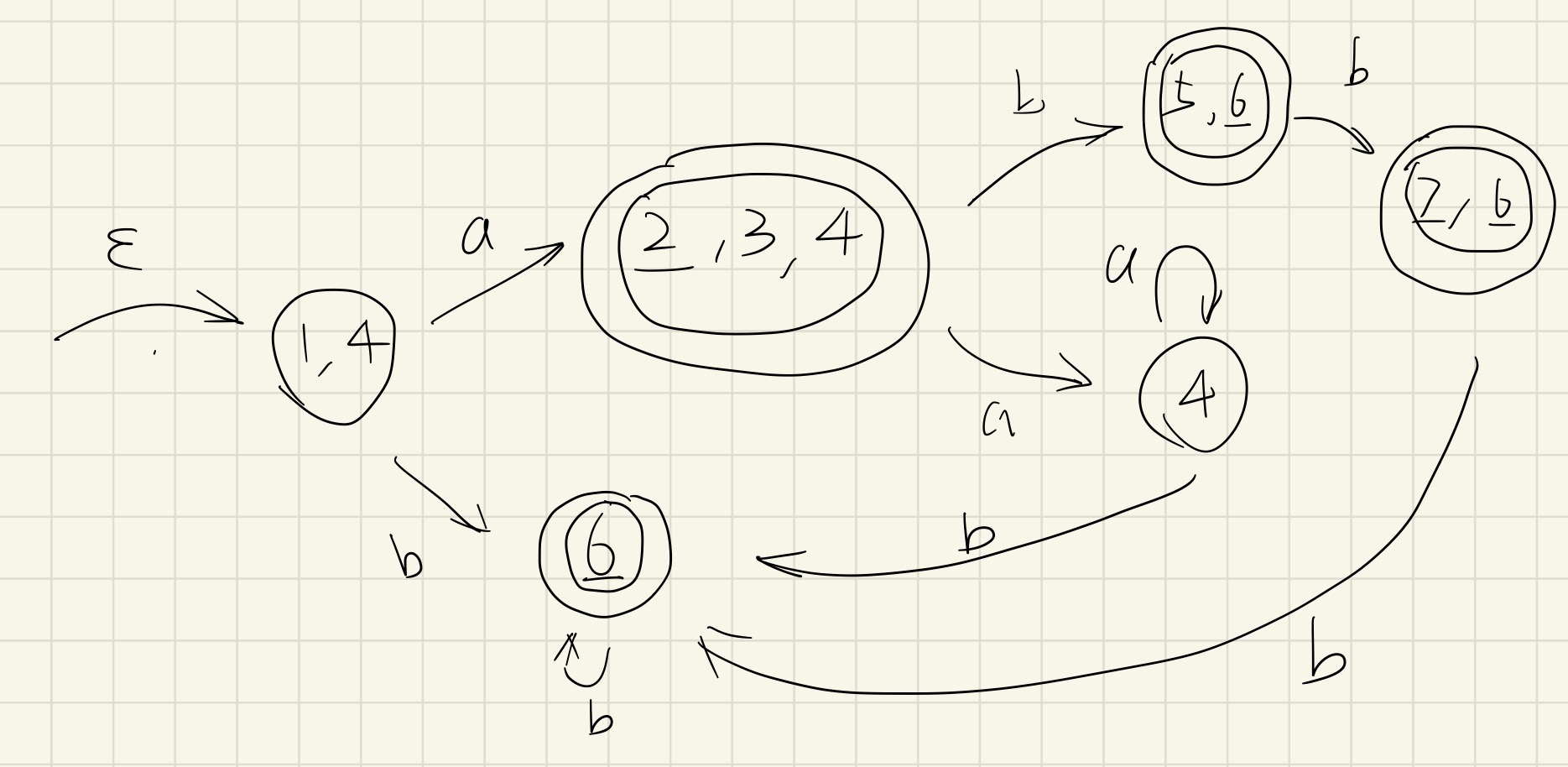
  • 在创建转换过程中，建议**逐一考虑** SS 中的每个状态编号的输入可能性，逐一的顺序由 NFA 中体现的优先级决定（例如 M∣NM|N 的 MM 优先级更高一点）；
  • 建议使用 BFS 的方法创建转换过程；
  • 在创建转换过程中，如果某个状态是终态，则在它的状态号下方标记下划线（方便识别），S′S^{\prime} 集合中元素以逗号隔开；
  • 一个 S′S^{\prime} 状态集合中只要有一个状态编号有下划线（是终态），则这个 DFA 状态为终态；不满足则不是终态；
  • 如果 SS 到 S′S^{\prime} 中有一个状态编号是相同的，但不完全相同，就不能用自环表示。例如上面的 {7,6}→a{6}\left\{7,6\right\}\rightarrow^a\left\{6\right\}，因为状态 7 没有任何非空输入能让它转换状态，所以用自环是不恰当的；
  • 最终 DFA 执行是停在非终态 / ERROR 终态，则解析错误；停在正确的终态中，从左到右（遵循优先级）考虑有下划线的状态编号，作为解析的结果。

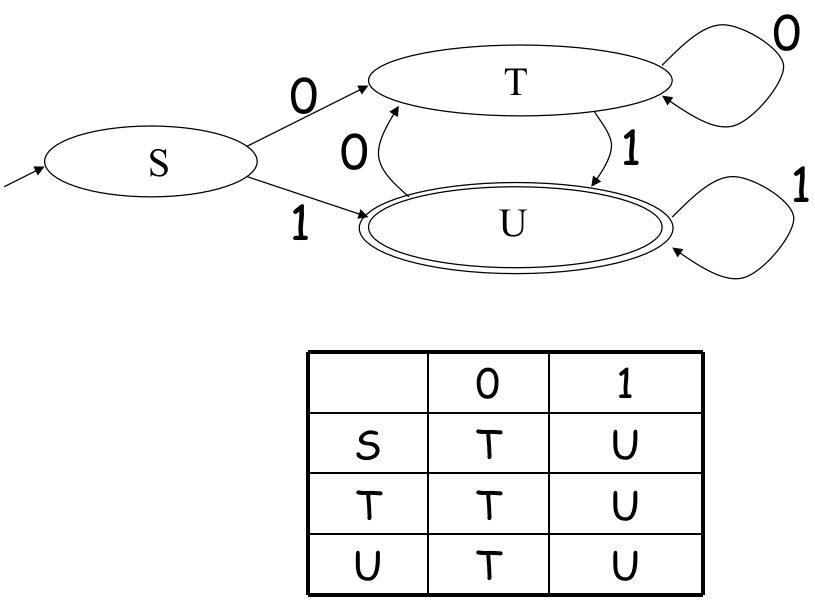
1.4.4 DFA to Table​

一个 DFA 可以被表示为一张 2D 的表格。其中一维存放所有 states，另一位存放所有可能的 Symbols，数学表达为 T[statet, input]=statet+1T[\text{state}_t,\text{ input}]=\text{state}_{t+1}；

这样能方便计算机执行一个 DFA：通过查找 statet\text{state}_t 和下一个输入符号，就可以跳转到确定的 statet+1\text{state}_{t+1}；

例如：

1.4.5 The Execution Rule of a DFA​

首先明确三种标记：

给定几个规则：

  • 初态时，三种标记（分别记为 IPLF、CIP、BCL）都位于第一个位置；

  • 接受输入时，current input position（记为 CIP）向前移动、更新当前状态（一般使用 state ID 数字）；如果移动后的状态是终态，那么也将 “input position at the last final”（记为 IPLF）移动到该位置；

  • 当输入符号不在 DFA 的当前状态的出路径中 / EOF，总之是无路可走时，则立即检查 IPLF 所处的最终状态（可以是有效，也可以是 Error）；

    • 如果正确，则取得 BCL 到 IPLF 间的字符为一个 Lexeme，并返回；

    • 如果错误，则输出错误信息；

    • 无论是正确还是错误，解析完这个 lexeme 后，立即更新 BCL、CIP 到 IPLF 的位置，将当前状态重新置为状态机的初始位置；

      如果在重置之后立即遇到 EOF，则文件解析完成，退出解析程序。