机器学习
机器学习Chapter 0. 概念Chapter 1. 线性回归Chapter 2. 决策树 & 随机森林Chapter 3. 贝叶斯分类 (朴素贝叶斯网络)Chapter 4. Naive Classification Algorithm: KNNImprovementsHyper-parametersUniversal ApproximationSummaryChapter 5. Linear Classifier: Logistic Regression5.1 核心概念5.2 线性分类器的基础模型:感知机(Perceptron)5.3 逻辑回归:从硬决策到概率估计5.4 多分类:Softmax 回归(多项式逻辑回归)5.5 二分类 与 多分类:SVM LossChapter 6. Multi-layer Perceptrons6.1 基本概念6.2 激活函数6.3 MLP 中的优化算法:反向传播6.4 深度学习与 MLP6.5 总结Chapter 7. Language Model7.1 词的表示方法:从离散符号到向量表示7.2 Word2Vec:词嵌入 (Word Embeddings) 的经典框架7.3 LM Basics7.4 神经网络语言模型与循环神经网络(RNN)7.4.1 基本概念7.4.2 训练方法7.4.3 总结Chapter 8. Transformer & Attention8.1 从 RNN Encoder-Decoder 到 Attention 机制8.1.1 基本概念8.1.2 训练方法8.1.3 思考与总结8.1.4 改进:Cross Attention (Encoder-Decoder Attention)8.2 Self-Attention: Transformer 的核心组件8.3 Transformer 架构8.4 总结Chapter 9. Large Language Model (LLM)9.1 预训练语言模型:从 BERT 到 GPT9.1.1 BERT: Bidirectional Encoder Representations from Transformers9.1.2 自回归架构9.1.3 GPT: Generative Pre-Trained Transformer9.2 微调 Fine-Tuning9.2.1 微调的核心逻辑9.2.2 参数高效微调(PEFT)技术9.3 提示工程(Prompt Engineering):解锁 LLM 的关键9.4 检索增强生成(RAG):弥补 LLM 知识局限Chapter 10. CNN & CVChapter 11. Computer Vision11.1 语义分割11.2 目标检测11.2.1 两阶段检测:R-CNN 系列的演进11.2.2 端到端检测:YOLO(You Only Look Once)11.2.3 图像字幕生成:从编码器 - 解码器到注意力机制11.2.4 视觉语言模型(VLMs):多模态融合的前沿11.2.5 扩展知识11.2.6 总结:计算机视觉的演进脉络Chapter 12. 无监督学习12.1 Clustering & K-Means12.1.1 基本定义12.1.2 K-means 算法的原理与步骤12.1.3 K-means 的关键问题与优化12.1.4 K-means 的优缺点与应用场景12.1.5 K-means 与其他聚类算法的对比12.2 Dimensionality Reduction12.2.1 背景:维度灾难(The Curse of Dimensionality)12.2.2 线性降维算法:PCA 主成分分析12.2.3 非线性降维:自动编码器(Auto-encoder)12.2.4 降维算法的延伸与前沿12.3 深度生成网络12.3.1 生成对抗网络(GAN)典型架构与变种12.3.2 变分自编码器(VAE):概率视角下的生成与压缩核心思想:潜码的概率约束12.3.3 扩散模型(Diffusion Models):从噪声到真实的逆向生成Chapter 13. 强化学习13.1 机器学习分类与强化学习定位13.2 强化学习基础框架:马尔可夫决策过程(MDP)13.2.1 核心概念13.2.2 值函数方法 (Value Learning):Q-learning 与深度 Q 网络(DQN)13.2.3 策略梯度方法 (Policy Learning):直接优化行为策略13.2.4 案例解析:AlphaGo 的混合智能框架13.2.5 强化学习在自然语言处理中的应用
Chapter 0. 概念
人工智能:能够处理⼀般需要⼈类知识和智⼒介⼊任务的计算机系统;
机器学习:从若⼲输⼊输出样例中学习数据规律的统计技术。按照 Tom Mitchell 的定义是从经验中自动改进系统性能的程序。经验常以数据的方式呈现,因此实践上机器学习为数据分析提供了主要工具。
深度学习:⼀种⾃动学习数据表征的机器学习技术;
机器学习是一种人工智能技术,使机器能够在无需显式人工编程的情况下,通过从数据中自动发现潜在的统计规律(模型),并不断优化自身性能(优化),以实现特定的目标(如最小化损失函数)。
本质上是通过优化方法挖掘数据中规律。
早期人们根据一些思想提出了不同的优化算法,如最近邻模型、决策树模型、贝叶斯模型、线性模型、多层神经网络模型。
而在 2012 年左右,人们提出了一类新的结构化的多层神经网络模型,学习效果显著。因此为区别传统的模型,使用这一类深层神经网络模型的机器学习方法被称为深度学习。
而数据表示的 “经验 / 规律” 可以包含不同的信息形态,其中比较关键的是关于模型表现的反馈信息。按照反馈信息的不同,机器学习经典划分为下面三大类:
我们现在就会发现,深度学习和强化学习的概念是重叠的。前者强调通过多层神经网络模型的方式达到机器学习的效果;后者强调 学习的环境、学习的方式,因此后者可以利用前者的思想/算法来达到目的(如 “深度强化学习”)。
机器学习 4 要素:
数据(经验)
模型(假设)
损失函数(目标)
优化算法(提升)
机器学习分类:
监督学习:学习器的每个输入样本都有一个目标输出标签。或者说处理包含有模型正确输出值的数据,即有标记数据。
目标:学习函数映射;
如分类问题、回归问题、目标检测、语义分割等;
例如例如图像识别数据中,每一张图像都有相应分类标记;
监督学习的两个前提:
输入的测试集(标注的数据)都应是没有关联的,满足独立同分布;
每个测试集都有明确的正误标签。学习机(learner)可以通过正确或错误的信息来修正预测;
无监督学习:Training examples as input patterns, with no associated output. 数据中完全没有关于模型输出好坏的客观评估。这时通常会人为的设置某种学习目标,以开展学习;
目标:学习数据隐含或潜在的结构;
如聚类、降维和特征选择、数据的概率密度估计、数据⽣成、异常检测;
例如把 256 维人脸照片压缩到 4 维,此时并没有任何关于这 4 维应该如何的信息,一种做法是使得这 4 维能够还原出 256 维的人脸,这就是一种人为设定的目标;
强化学习:通过与环境交互来学习。处理的数据仅包含有模型打分值,而不知道模型到底应该输出什么(环境很复杂)。因此只能靠算法去不断的探索,寻找打分值最高的模型输出;
目标:学习状态(states)到动作(actions)的映射,以最大化长期奖励(reward)。
例如围棋游戏,缺乏每一步走棋的最佳指导,只能通过最终的输赢作为打分,自主探索寻找最佳模型;
数据归一化:
Z-score normalization: rescale the data so that the mean is 0 and the standard deviation is 1.(数据集归一化为均值为 0、标准差为 1):
Min-max normalization: scale the data to a fixed range of [0, 1].(将数据集映射到
泛化性与过拟合:模型应该学习普遍的规律还是记住特定细节?
欠拟合:因模型不够复杂无法刻画真实规律,模型假设可能不成立;
过拟合:因模型过于复杂导致记住数据的细节(如随机噪声)而不是潜在的规律;
避免过拟合;就是选择合理复杂度的模型。常见避免过拟合的方法:
增加训练数据;
正则化 (惩罚模型复杂度);
数据划分 & 交叉验证 (训练时用未知数据测试确保泛化能力);
早停;
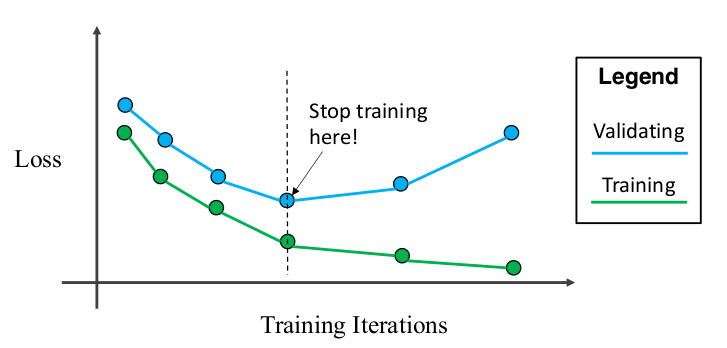
引入先验知识 (如贝叶斯先验);
……
Chapter 1. 线性回归
考虑监督学习中的 “回归问题”。
目的:通过大量观察,回归到统计数据的真实情况。
定义:A function that describe the relationship between one dependent variable and a series of other (independent) variables.
应用:预测、归因分析、控制;
模型核心:简单的线性函数
训练过程:根据数据误差估算合适的
预测过程:根据输入的新数据计算回归值。
损失函数:对于完整数据集
r 为预测值,y 为 ground truth;
训练优化:梯度下降。目标:
结论:计算解析梯度可知,
; 预测值
,损失函数: ; 梯度
;最优参数 ; 代入预测值:
;
Chapter 2. 决策树 & 随机森林
再考虑监督学习中的 “分类问题”。
如何构建决策树?
构造一个根节点,包含整个数据集;
选择一个最合适的属性,根据选择属性的不同取值,将当前节点的样本划分成若干子集;
对每个划分后的子集创建一个孩子节点,并将子集的数据传给该孩子节点;
递归重复 2~3 直到满足停止条件;
按照不同划分顺序,同一数据可以构建多种不同的树。
如何高效率地构建决策树?选择每个属性 X 的时候,尽可能最大化标签 Y 的纯度。
决策树将数据逐步分割成越来越小的子集。最理想的情况是叶节点对应的样本属于同一类别(节点的标签纯净)。
如何选择属性以最大化标签的纯度?选择 X 以最大化 信息增益、Gini 系数等(每⼀种指标对应⼀种决策树构造算法)。常见算法如 ID3、CART、C4.5 等等。
ID3 算法。划分属性使最大化信息增益 (Information Gain)
试着对每个属性进行划分,看看哪个划分效果“最好”,评价标准为样本的整体信息熵的降低程度。
停止划分条件:纯度(叶结点样本属于同一类)、数据量过小(叶结点样本数少于阈值)、没有属性可分。
优点:易理解, 可解释性, 便于可视化分析;数据预处理要求低,可以轻易处理非线性边界;数据驱动,可以以任意精度拟合训练集。
缺点:容易过拟合,某些噪声样例总能被树涵盖并学习。
随机森林。将数据随机划分子集,各自构建决策树,将结果合并。
往往比决策树更准确;
训练速度快, 容易并行化 (训练时树与树之间是相互独立的);
可以处理高维数据,并且不用做特征选择 (因为特征子集是随机选择的);
可以处理缺失属性;
结果易解释 (i.e.,在训练完后,能够给出哪些feature比较重要);
在训练过程中,能够检测到feature间的互相影响;
对于不平衡的数据集来说,它可以平衡误差;
Chapter 3. 贝叶斯分类 (朴素贝叶斯网络)
考虑从概率学角度解决分类问题。
多条件下:
我们需要构建一个
不过我们做一些概率学变换:
我们作出假设:假设给定的特征(维度)间相互独立。在这个假设下,我们有:
这样可以用频率简单地估计每个
为了解决 zero count 的问题(任何一个
这被称为 Laplace Smoothing;
最终对输入
优势:
快:
on training, requires only a single pass over the training set;
on testing, also fast;
performance 优异:
当数据大致满足独立前提时,效果卓越;
多分类问题上表现不错;
新增/删除数据集时只需要加减,易于维护;
劣势:
很多数据集的各个维度实际相互关联,通常违背独立假设;
但是通常效果也不错,因为我们不需要
计算正确,只需要:
Chapter 4. Naive Classification Algorithm: KNN
先来个最简单的算法(甚至不配叫深度学习算法):最近邻。
trainphase 直接记录所有训练数据;predictphase 将输入数据与所有训练数据逐个比较,确定最近的图片对应的 label;定义两个图片距离:
Manhattan Distance(曼哈顿距离):
Minkowski Distance(闵氏距离):
相似度(如余弦相似度):
算法描述:
选取邻居数
对测试集中的每个需要被分类的样本
按距离数据排序,取最近的
这个方法有致命缺陷:训练
此外,使用曼哈顿距离并不是很聪明(只是把看起来相近的图片归为一类,例如白色背景的猫和白色背景的青蛙会被归成一类)。
我们引入 decision boundaries(决策边界)来描述,这幅图被称为 Voronoi Tessellation(维诺图,沃罗诺伊分割):
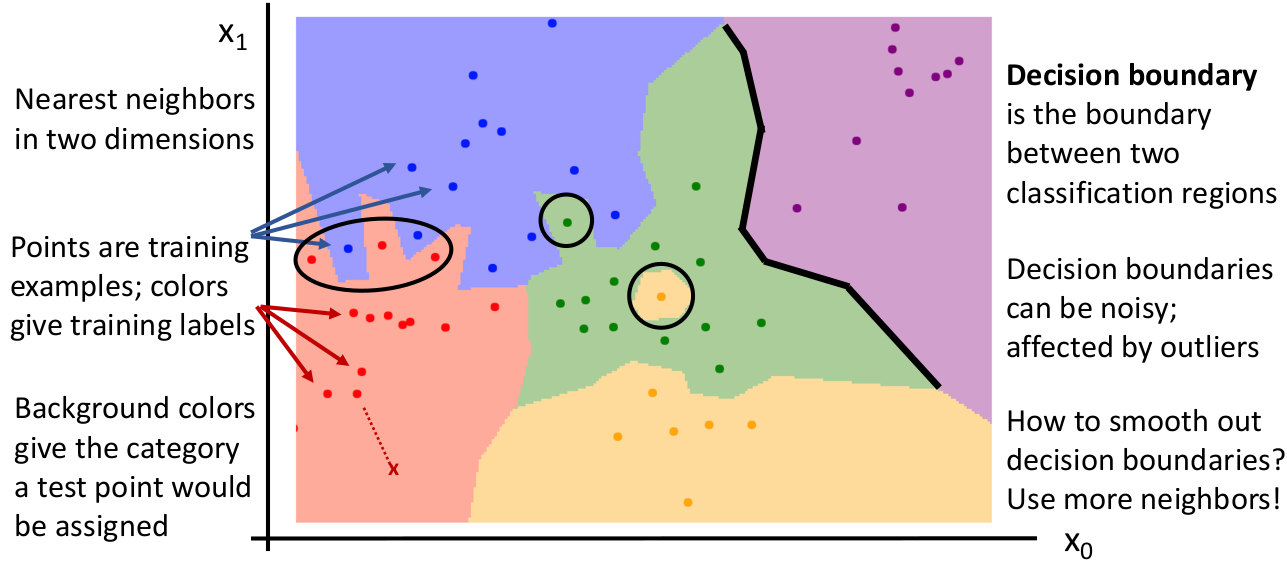
对于一个二维数据(例如 2 个像素的图像),点代表训练集,颜色代表标注的 labels。没有标注点的是其他的可能数据。而黑线就是按照模型算法判断的决策边界。所谓区分两个类型就是确定两个类的决策边界(黑线)。下次测试输入数据时查看落在哪块区域内即可。
某些异常情况(例如噪点)可能导致真实的分类边界参差不齐。
Improvements
改进 1:为了解决最近邻不准确的问题(直接使用最近邻居的 label),我们引申出 K-Nearest Neighbor(KNN),从 K 个最近邻居中选出得票最多的 label 作为测试数据的 label。这个改进我们可以从决策边界图看到:
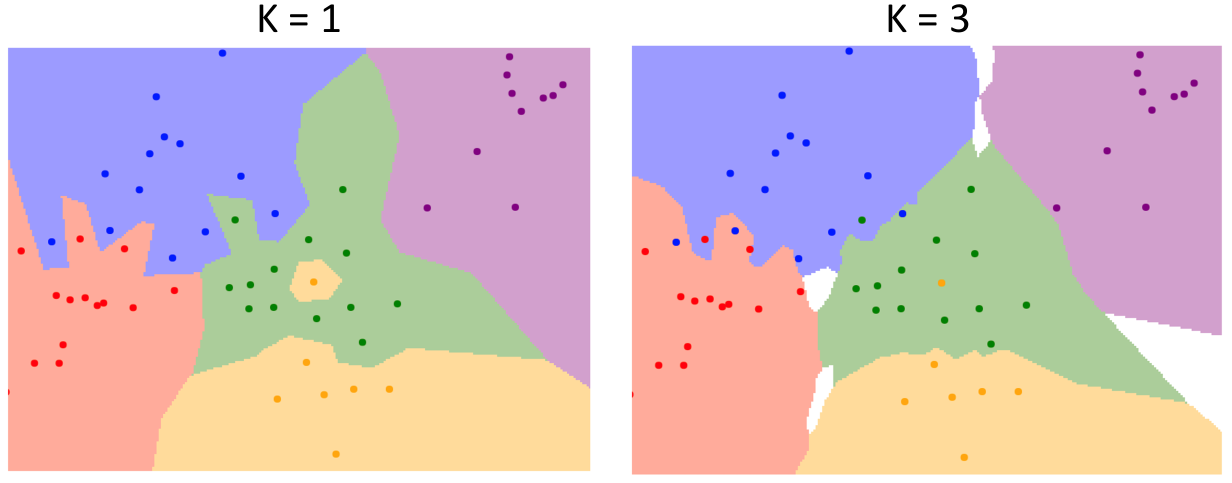
可以看到,这使得模型的决策边界变得平滑,并且减小了测试数据受到个别噪声点的影响。
但 K-Nearest Neighbor 的问题是可能存在投票平局的问题,此时在图中显示是空白的颜色。你可以使用 heuristics(例如 fall back 到一个的情况)。
总结:
K 过小:算法效率提升,但更易受到噪声点的影响;
K 过大:算法效率不高,且包含太多其他类的 votes,over-smoothing 分类结果,模型效果不佳;
改进 2:更改 Distance Metrics。在 KNN 的基础上,我们将判断图像相似度的距离指标从曼哈顿距离(
曼哈顿距离的边界都是由垂直或水平或 45 度倾角的线段组成;而欧几里得距离的边界虽然还是由线段组成,但是可以朝向任意方向(相当于用计算量换取更灵活准确的分类方式)。
这里虽然看不出来二者的优势究竟在哪,但是这告诉我们一个好消息:对于任何一个数据类型,只要给一个 distance matrics,就能将 KNN 算法应用上去!例如衡量两个 PDF 文件的相似性(作为 distance),可以使用 TF-IDF(Term Frequency-Inverse Document Frequency,词频-逆文件频率)similarity,它通常被用在一些 NLP 应用中。
TF-IDF 指出,字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降。
前者因为它更能代表一篇文章的主题,后者因为它更有可能是停用词、或者是不能很好作出区分的词汇。
这再次证明了,不考虑性能的情况下,调整 KNN 的距离指标计算方法可以在不同的应用场景下获得很好的分类效果。
Hyper-parameters
另一方面,除了 training data,还有一类参数例如 邻居数 K、最佳的距离指标(各种距离还是其他算法?),它们被称为学习算法的 “超参数”(hyper-parameters),意指在训练前就应该为学习算法确定的(而不是训练时获得),能对算法的运作方式产生间接深远影响的参数。
通常情况下,超参数的最优取法与具体问题有关,没有 silver bullet;有几种做法:
做法 1:使用全部数据作为 training data,并选对自己训练的数据集而言 accuracy 最大(最佳)的超参数;
这是不行的。以 KNN 为例,我们会永远选择 K=1 的情况,因为总是和训练集数据自身比;
做法 2:将数据分为
training和test,使用training来训练,但选择对test而言 accuracy 最大的超参数;使用机器学习的目标之一就是要 generalize 到未知的数据,因此这么做是更合理的。
但这也是不行的,和上一条一样是有问题的。这会导致对你的模型表现的错误预估。
因为这不是单纯的 evaluate,而是设置超参数。这么做会导致模型仍然会被所谓的 “unseen data” 的知识所污染(你还是参考了 unseen data 来对算法的超参数作出了决定),模型和上面的一样,不能对真正未知的数据有足够的泛化性。
做法 3:将数据分为
training、validation和test,使用training来训练、validation来确定最优超参数,test来做最终一次的 evaluation;这条是真正比较科学的做法。不过还有更科学的做法。
做法 4:cross-validation;将数据分为 N 个
fold,以及一个test,遍历每个 fold,将每个 fold 作为一次validation set,然后除了它和test的剩余部分做training,如此得到 N 个不同的最佳超参数,然后根据某种策略(如最大 accuracy / 超参数平均值等)选取最好的超参数。理论上这条比上一条更好,但是需要的计算量也更大。
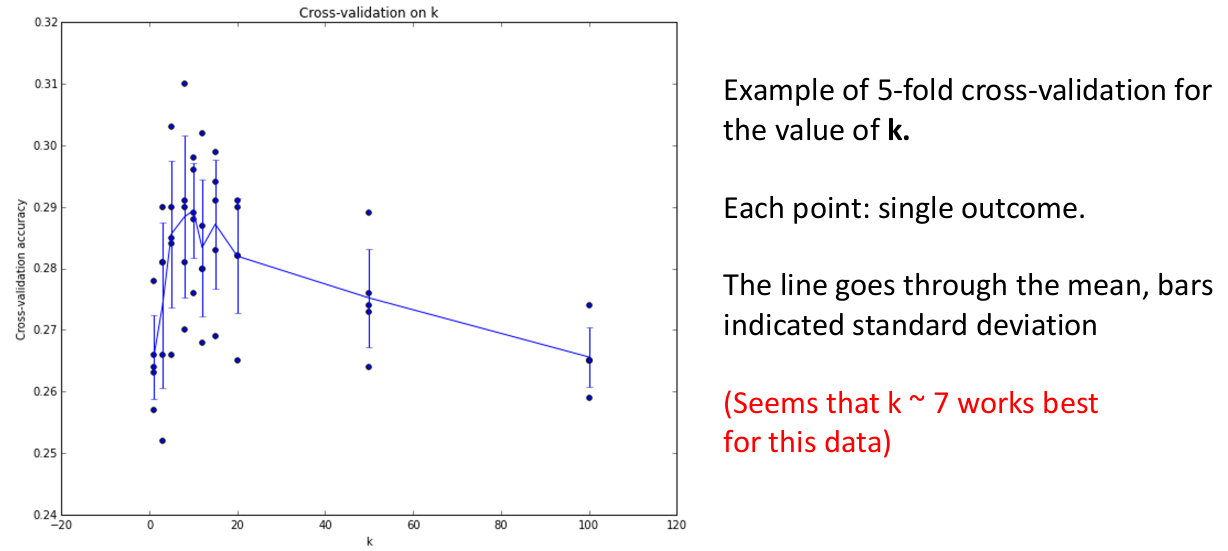
如上图是 5-fold cross validation 模式训练的 KNN 模型在超参数
Universal Approximation
由于 KNN 对于处理的函数几乎没有做前提假设,因此在训练集大到接近无穷时,KNN 甚至可以表示几乎任何常见的函数(有点像泰勒级数的逼近)。
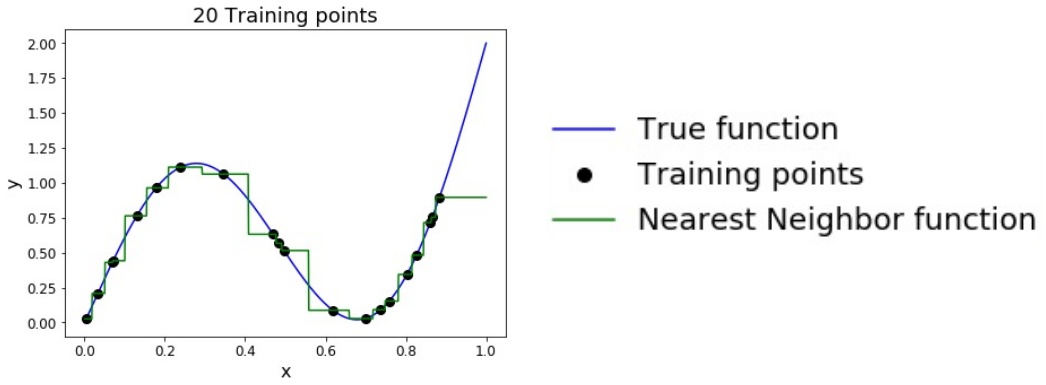
问题是随着维度的增加,需要逼近真实解到同样程度的训练集大小会呈指数级增加,这被称为 “curse of dimensionality”(维度诅咒)。这是不可接受的,因为上面图的情况仅仅是一维的数据。如果是一张 32x32 的图片,训练集大小的数量级会在
正因如此,KNN 在 raw pixels 的图像处理领域很少被用到,总结:
需要大量数据来达到不错的效果(维度诅咒);
distance metrics 在图像领域并不具有明显语义;
但某些情况下(不是 raw pixels)KNN 能很好的识别图像特征,例如在深度卷积神经网络计算得到的特征向量(特征提取)中进行 KNN 并以此做图像分类/看图说话等等,可以得到很好的效果(从容应对 various viewpoints、bg clutter、illumination changes 等干扰因素),这个后面讨论。
Summary
优势:
容易理解、实现;
新数据可以直接添加到训练完的模型上,几乎不会损害模型精度、不需要从头训练;
劣势:
测试/推理性能极差,显然不能 scale 到大规模数据上(尤其是计算距离非常耗时);
维度诅咒;
空间占用大;
数据一般需要标准化后再传入;
Chapter 5. Linear Classifier: Logistic Regression
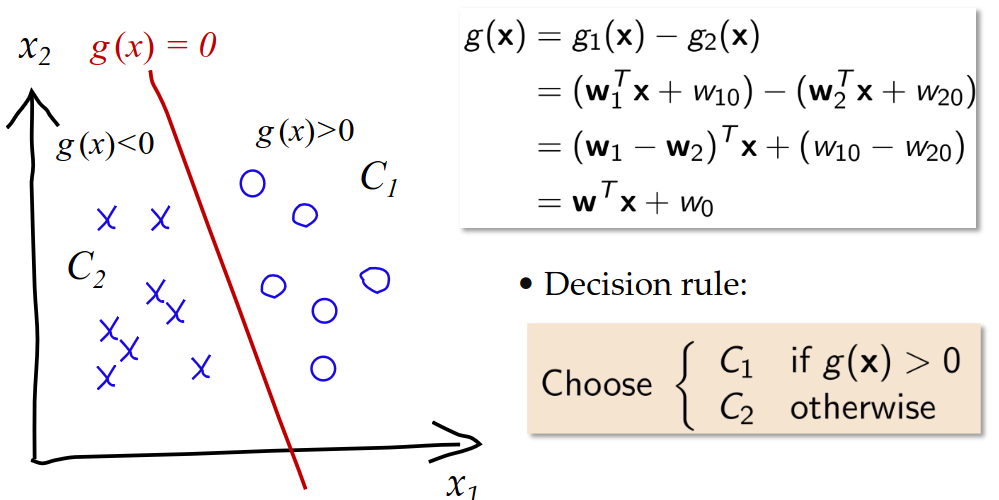
线性分类器,其核心思想是通过线性函数直接建模类别间的决策边界,相比估计数据密度(如贝叶斯)或距离(如 KNN),分类的效果更直接。
Determinizing class boundaries (discriminants) is usually easier than estimating the class densities.
5.1 核心概念
基于建模决策边界的分类器的核心,就是判别函数(Discriminant Functions):为每个类别定义一个函数
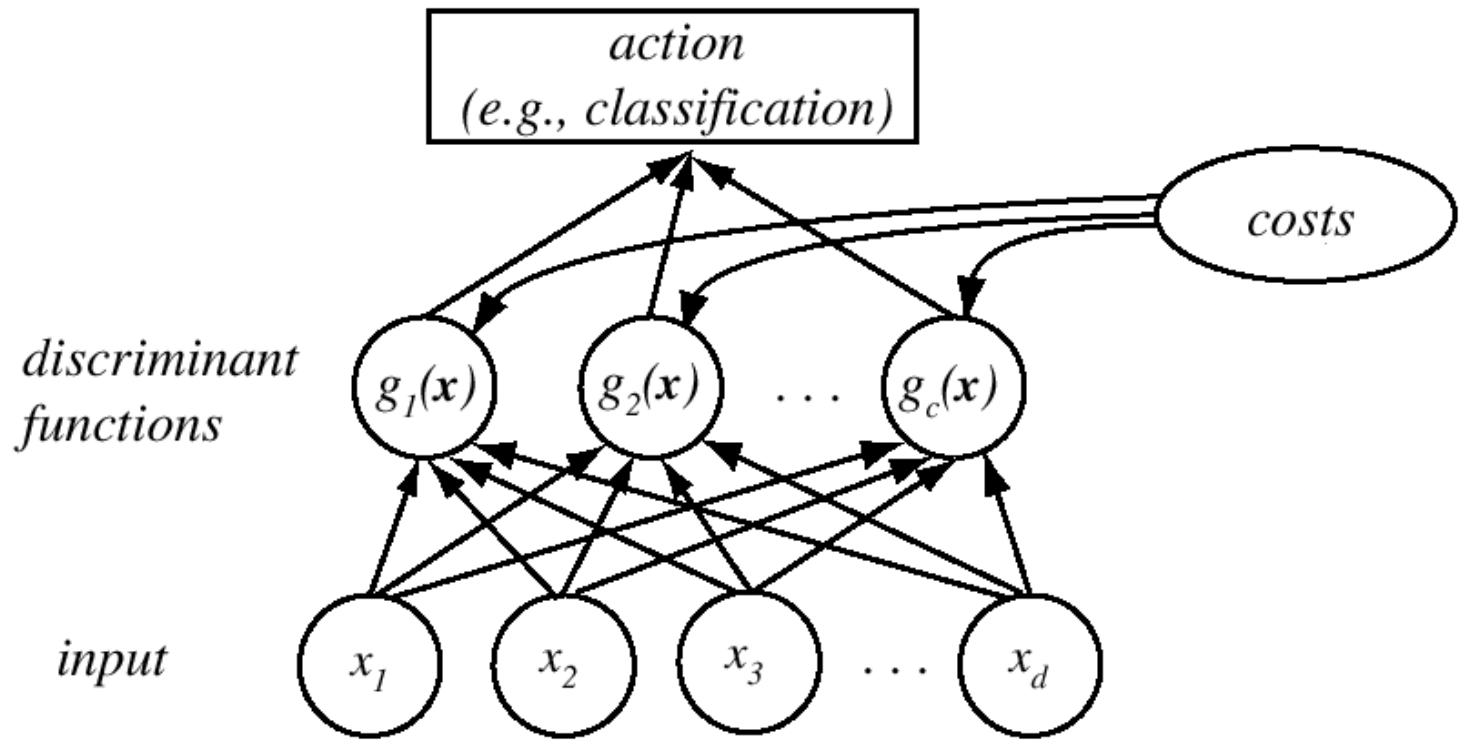
例如,贝叶斯决策可转化为
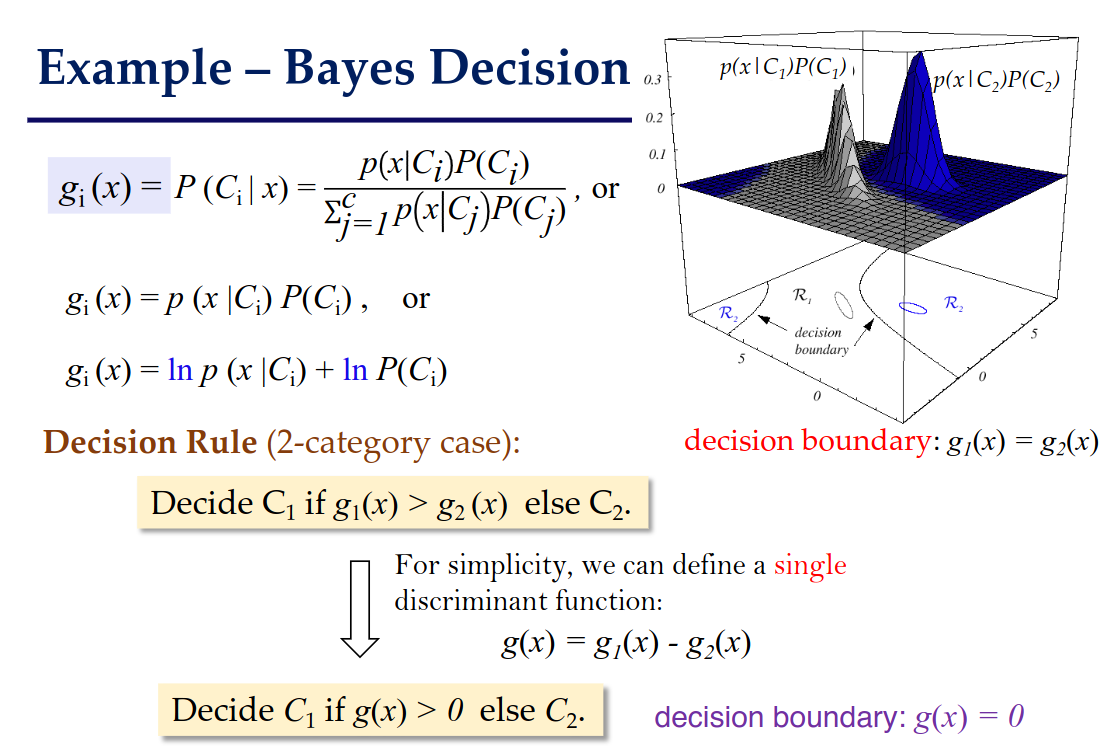
这章我们考虑简单情况,也就是判别函数是线性函数的分类器。它就是线性分类器。它的判别函数:
优势:
算法简单:
易于理解:输出的结果是类型/特征的权值;
精确:在一些 assumptions 满足的情况下非常精确;
以二分类为例,线性分类器的决策边界是超平面(Hyperplane),由
定义,形式为 ,将空间划分为两个半空间。
5.2 线性分类器的基础模型:感知机(Perceptron)
感知机是最早的线性分类器,其判别函数为
训练算法(感知机学习规则):
目标:通过数据估计参数
更新策略:对于误分类样本(即
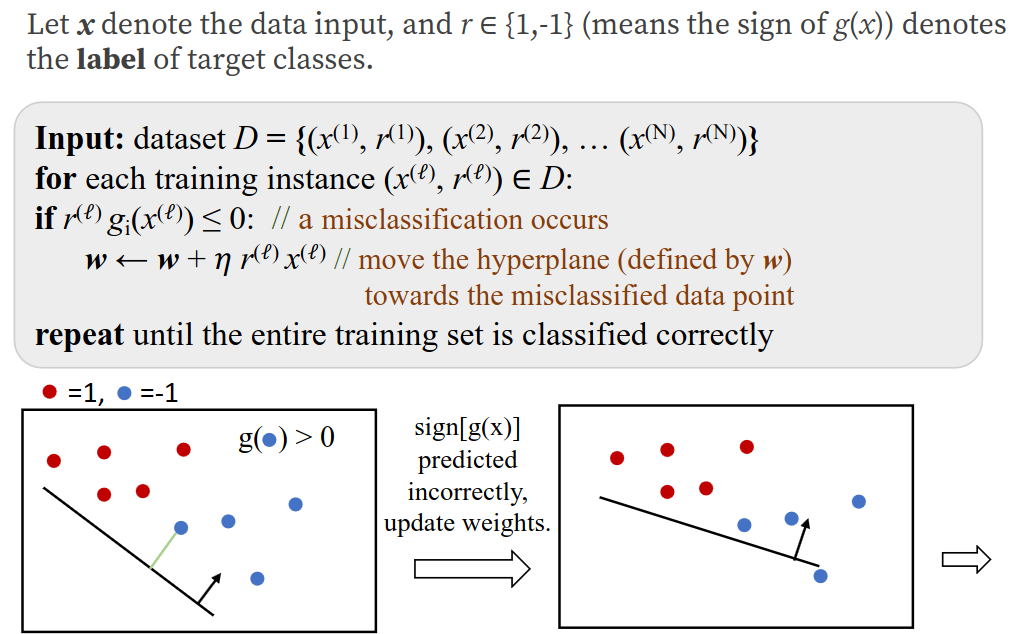
感知机的局限性:
硬决策问题:输出仅为 0 或 1,无法表示分类的置信度,且优化目标(完全正确分类)在非线性可分数据上可能不收敛。
无法处理复杂边界:仅能解决线性可分问题,对异或(XOR)等非线性问题失效。
知识补充:
香农(Shannon)认为,一个事件的不确定性(或者称 surprisal / self-information)越大,信息量就越大;重复的 Message 传递的信息量更少。他引入了衡量信息量的量 —— Shannon Information Content;一件发生概率为
的事件的香农信息量由下面的式子给出: 事件的信息由 SIC(香农信息熵)衡量,那么 随机变量的概率分布 的信息 由什么衡量?
假定
是一个有限样本空间 的一维离散型随机变量。其概率在各个值的分布为 ,那么定义:该随机变量所遵循的概率分布的信息量大小由 信息熵(Information Entropy)衡量,大小由下面的式子给出: 即离散型随机变量概率分布负对数的期望。信息熵越大,意味着随机变量的概率分布的不确定性越强(在一维离散型随机变量的概率分布中的体现就是,随机变量的每个可能取值的概率接近),说明它的信息量越大。
通俗地说,信息熵描述了有多少信息是无法确定的。信息接收了多少,熵就降低了多少。
或者说,熵是要消解事件不确定性的平均代价。
数学小提示:
你会在很多场合用到,可以通过换元法证明。简记为
0 log 0 = 0;高维离散型随机变量的概率分布是联合概率分布,以二维随机变量为例,联合熵定义为:
那么条件概率分布呢?这是我们已知条件(降低了信息熵)的基础上,求一件事物的信息熵。它的定义如下:
若
,则: 式子的含义是,在所有给定
的条件下的 的期望。根据定义求解的方法是,找到 和 ,代入公式即可。 如果是给定
的情况下(也比较好理解,上面的 定义式不对 求和、 更改成已知 的条件概率即可): 但是,最好理解的方法还是 “熵的含义”:熵是对事件的不确定性。我们已知了
事件的信息,就相当于消解了联合概率分布 中 的信息熵,也就是从两个事件的联合熵中减去了 的信息熵,推导如下: 所以条件熵第二种算法,也是最简单、最通俗易懂的计算方法,就是
减去 。 这就是信息熵的链式法则:
类比条件概率的链式法则:
说明熵的对数运算让乘除变为了加减。
以下是条件熵的特性:
等价于 完全取决于 ;
等价于 与 相互独立; 那么,再考虑一种情况。我们之前都是正确掌握了随机变量的概率分布,并用这些信息构建了概率分布的信息熵的定义。
如果对于一个离散型随机变量,我们并不知道它的具体分布、只是模拟了近似的概率分布。这样的信息和真正的概率分布有差距,那这个概率分布的不确定性又该如何描述?
人们定义了 “交叉熵” 的概念,用来描述:在实际概率分布为
,但却作出概率分布 的假设下,消解该随机变量不确定性的平均代价就是交叉熵,定义如下: 准确的定义是,对于同一个事件集上的两种概率分布
、 间的交叉熵,描述的是:如果编码方案采用针对 的优化,而非真实分布 的优化,那么平均需要从事件集中取出多少 bit 才能发现真实分布的情况。 这就相当于我们不知道
、但先当作 估计的时候,所要了解事件的真实分布需要的平均代价。 现在假设我们后来知道了
,那么我们由于原来作出的假设 分布,而造成与现实情况的偏差,导致要花费的更多的代价才消解不确定性。那么如何衡量这个代价的增量?这就是相对熵(Relative Entropy),又称 KL 散度(KL Divergence): 显然
; 数学上,可以用优化理论证明,
当且仅当 成立。 交叉熵和相对熵在机器学习领域(例如损失函数)使用颇多。它可以描述 当前估计的数据分布 相较于 真实数据分布 的偏差情况。
如果两个随机变量不是相互独立的,那么它们必定在概率和信息熵上相关联。
就是说,一旦两个随机变量不相互独立,那么得到一个随机变量的信息,就会影响另一个随机变量的信息熵(就是从熵的角度理解两个非独立随机变量的条件概率)。
如何描述这两个随机变量的 “信息关联性” 呢?
人们定义了 “互信息” 的概念:一个随机变量所携带另一个随机变量信息的信息量。这个携带的信息量越大,那么这两个随机变量的相关性越强。
这个定义的含义是,假设分布
(二者独立)相对于 真正的分布 的偏差代价。 除了直接计算
、 ,我们还能通过推论更直观的方法理解互信息: 两个信息熵相交的部分。
5.3 逻辑回归:从硬决策到概率估计
为了优化感知机的算法,我们需要将 “0-1” 硬决策转换成概率估计的值,这个时候就需要引入 sigmoid 函数:
优势:
输出范围在 (0,1) 之间,可解释为属于
函数平滑可导,并且数学特性方便求导,便于优化。
现在输出的并不是特定的类型,而是类似概率的值。为了方便模型参数优化,我们还需要为它定义损失函数,用来衡量决策的好坏。这里我们引入 “交叉熵” 损失函数(注意由于是二分类问题,
数学上注意到,这等价于最大化此式概率:
, ;
这样原问题转换为,确定让损失函数最小的
给定训练数据集
目标函数:
算法:梯度下降,向
w = initialize_weights()for t in range(num_steps): dw = compute_gradient(loss_fn, data, w) w -= learning_rate * dw注意到
xdef initialize_weights(): w = [] for i in range(d+1): w.append(random.rand(-0.01,0.01)) return w
def loss_fn(x, w, r): # 这里 w0 为偏置量 dw = r - sigmoid(w @ x + w0) @ x return dw
5.4 多分类:Softmax 回归(多项式逻辑回归)
对多分类问题,我们需要更改损失函数,以便输出
对任意一个样本-标签对
softmax 函数:
(之所以称之为 “softmax”,是指 “max” 函数的可导的近似函数,a soft differentiable approximation to hard max function);
可以让向量的各项介于 0~1 间,并且总和为 1(不至于像 max 函数一样大部分是 0,这使得网络中的一些计算难以进行);
可以借助指数函数特性(
),让两个不同的数值 大的更大、小的更小(凸显不同数据的差异); 其导数有很好的性质,方便计算交叉熵损失函数;
它在 “需要计算 max 特征”、“需要可导”的这些场景下比较有用。
注意到这是 softmax 函数。我们考虑模型对
我们回想一下,在概率学中,想要衡量 “在实际概率分布为
注意到
现在优化方法仍然保持不变(梯度下降),我们计算
总结线性分类器:
优势:计算高效(时间复杂度
劣势,线性分类器对于某些特定的数据类型没法很好地分类:
(从二维上看)分布在对角象限内的类型数据。(不可能用线性超平面完美切分)
在欧式超空间中,一类数据分布为离散的不同聚簇中。(不可能用线性超平面完美划分)这恰好可以对应前面我们说 “同一类别的不同模式”,例如马的不同朝向;
在欧式超空间中,以半径为特征分布的类型。(不可能用线性超平面完美划分)
或者说:
线性可分假设:若数据无法用超平面划分(如 XOR 问题),线性分类器性能较差。
多解问题:即使数据线性可分,可能存在无数超平面实现分类,需额外约束(如 SVM 的最大 margin)来确定最优解。
补充:
逻辑回归与线性回归的联系:线性回归直接预测连续值,而逻辑回归通过 sigmoid 函数将线性组合转化为概率,本质是 “广义线性模型” 的一种;
为什么用交叉熵而非均方误差(MSE):若对逻辑回归使用 MSE,损失函数可能非凸且梯度消失,而交叉熵基于似然估计,能保证凸性和有效优化;
线性分类器的 “softmax classifier” 和 “sigmoid classifier” 比较:逻辑回归广泛用于二分类问题(如垃圾邮件检测、疾病诊断),Softmax 回归用于多分类(如手写数字识别、文本分类)。
5.5 二分类 与 多分类:SVM Loss
多分类问题,除了 softmax 作为损失函数,还有一种损失函数是 multiclass SVM Loss。这个损失函数的思想是,正确的类型的得分,会远远高出不正确类型的得分。即不关心具体得分,只关心能否给出准确的 label。
通俗的来说,就是要最大化两个类别间的 margin(得分差)。
注:我们将使用 Multi-class SVM Loss 作为损失函数的线性分类器称为 “SVM classifier”;
对于一个图像样本
Multi-class SVM Loss 给出:一个算法对 “ground truth 的得分大小和其他错误类比的得分大小关系” 与损失值的关系。绘图如下:

解读:当一个算法对 ground truth 判断的得分高出其他错误得分的差值越小(小于 margin 时),损失值会线性增大。
这种含有线性区域和零区域(水平区域)图像的损失函数,被称为 “Hinge Loss”(看起来像 door hinge);
我们记
因此这个损失函数的数学表达式可以写成:
解读:所有对于任意样本
,评分系统 在 上的损失 由所有不正确类型的得分( )和 ground truth 得分( )决定。 意味着只有正确类别比其他每个类别得分都要高出
才能实现无损失。 注意到:在一开始没有进行训练时,一个样本的损失值大约为
,其中 为分类数。因为 ; 为什么需要知道这个?因为我们需要一些 debugging 的手段(大概知道自己的模型有没有写错)。
显然,
拓展:
应该设置成什么值,是否需要 cross validation?这里先给出答案,你可以先看 “正则化” 一节后再来理解: 事实证明,在任何情况下都可以放心地将这个超参数设置为
。超参数 和正则化参数 似乎是两个不同的超参数,但实际上它们控制着相同的权衡:目标中 Data Loss 和正则化损失之间的权衡。理解这一点的关键在于,权重 的大小对分数(以及它们之间的差异)有直接影响:当我们缩小 W 内的所有值时,分数差异会变小,而当我们扩大权重时分数差异就会增大。因此确切值(例如 或 ) 在某种意义上是没有意义的,因为权重可以任意缩小或拉伸差异。因此,唯一真正需要权衡的是正则化参数 )。
Tips 1:如果把上面损失函数的求和换成求平均,这个分类器会不会有明显变化?答案是不会,因为将所有样本损失值同时乘以
Tips 2:如果将损失函数换成
Tips 3:假设我们找到一个
实际上 SVM 尤其擅长解决二分类问题(毕竟它的语义就是从二分类出来的)。
考虑 SVM 解决二分类问题:


对于线性二分类问题,SVM 可以将其转换为二次规划,是个凸问题,意味着 SVM 总是能找到最优解!
下面是一些线性二分类 SVM 的计算结论(损失函数完整表达式、梯度下降时会用到的梯度计算式):

Chapter 6. Multi-layer Perceptrons
6.1 基本概念
单层感知机:
单层感知机的数学定义
基本结构:输入
用途:回归(
单层感知机的局限性
Minsky 和 Papert 在 1969 年证明:单层感知机无法解决 XOR(异或)问题,因为 XOR 数据非线性可分。
例子:AND 和 OR 问题线性可分,而 XOR 需要非线性边界。
MLP 的结构与原理:
核心:在输入层和输出层之间添加隐藏层,通过多层非线性变换处理复杂模式。
万能近似定理(参见另一份笔记):含一个隐藏层的 MLP(足够多隐藏单元)可近似任何连续函数。
例子:XOR 问题可通过 “
隐藏层的作用:
将输入空间非线性变换到高维空间,使数据在新空间中线性可分。例如,通过 “挤压” 和 “变形” 处理非线性边界问题。
模块化学习:底层隐藏单元学习基础特征(如边缘、颜色),高层组合为复杂特征(如物体部件)。
6.2 激活函数
常用激活函数
Sigmoid:
ReLU:
Tanh:
其他:Leaky ReLU、ELU、Swish 等,各有针对性优化(如负数区域的梯度问题)。
激活函数的作用
若不使用非线性激活函数,多层网络等价于单层线性模型,无法处理非线性问题。
6.3 MLP 中的优化算法:反向传播
参见另一份笔记。需要训练计算。
6.4 深度学习与 MLP
深度学习的定义与特点
核心:通过多层神经网络自动学习数据的层次化表示,从底层特征(如像素)到高层抽象(如物体、语义)。
与传统机器学习的区别:传统方法依赖手工设计特征,而深度学习通过端到端训练自动提取特征。
深度网络的优势
模块化:底层特征可共享(如边缘检测),高层特征针对具体任务(如 “猫” 的耳朵、尾巴)。
数据效率:深层网络用更少参数实现更高复杂度,适合大数据场景。
MLP 的局限性与后续模型
不足:参数过多易过拟合,无法处理序列数据(如语音)和空间结构(如图像)。
进化模型:卷积神经网络(CNN)处理图像,循环神经网络(RNN)处理序列,Transformer 成为当前主流。
6.5 总结
MLP 的核心价值
作为深度学习的基础模型,证明了多层非线性网络的强大表达能力,为 CNN、RNN 等奠定理论基础。
实践要点
激活函数选择:优先 ReLU,避免 Sigmoid 在深层网络中的梯度消失;
训练技巧:使用批量归一化(BatchNorm)、dropout 等缓解过拟合;
工具推荐:PyTorch、TensorFlow 实现 MLP 与反向传播。
Chapter 7. Language Model
7.1 词的表示方法:从离散符号到向量表示
传统词表示方法
离散符号表示:早期计算机用 ASCII、ID 等离散符号表示单词(如 “hotel”=11,“motel”=1203),这种 “局部表示”(Localist Representation)无法捕捉语义关系。
One-Hot 编码:将单词表示为高维 0-1 向量(如 “tree”=[0,0,0,1,0,...]),向量维度等于词汇表大小(如 50 万维)。但该方法存在两个问题:
维度灾难:向量稀疏且维度极高;
无法表示语义相似性:任意两个 One-Hot 向量的余弦相似度为 0(如 “hotel” 和 “motel” 语义相近,但向量无关)。
词嵌入(Word Embeddings)的提出
定义:将单词映射为低维稠密向量(如 50-300 维),向量距离反映语义相似性(如 “hotel” 和 “motel” 的向量接近)。
优势:能捕捉词汇的语义结构,例如:
性别关系:man - woman 与 king - queen 类似;
时态关系:walked - walking 与 swam - swimming 类似;
国家 - 首都关系:Spain-Madrid 与 Italy-Rome 类似。
7.2 Word2Vec:词嵌入 (Word Embeddings) 的经典框架
核心思想:“词由上下文定义”(J. R. Firth 1957)。通过上下文预测中心词(或反之)来学习词向量。例如,根据 “a bottle of tesgüino is on the table” 等句子,可推断 “tesgüino” 是类似啤酒的酒精饮料。
于是 Word2Vec 框架(Mikolov et al. 2013)的思想就出来了:Two words are similar if they have similar word contexts。
我们有一个庞大的文本语料库。
词汇表中的每个词都有一个可学习的向量;
查看文本中的每个位置
,其中有中心词 和上下文词 ; 利用它们的向量相似性计算出
给定 的概率; 不断更新词向量,以最大限度地提高这一概率。
目标:在大规模语料库中,通过最大化 “上下文 - 中心词” 的共现概率来学习词向量。
窗口机制:以中心词为中心,取左右各 k 个词作为上下文(如窗口大小 2 时,上下文为中心词前后各 2 个词)。

Word2Vec 框架下的著名模型就是 CBOW(Continuous-Bag-of-Words,连续词袋模型)了。
实现:用上下文词的向量预测中心词。例如,输入上下文词的 One-Hot 向量,通过嵌入矩阵映射为稠密向量,聚合后(如平均)输入神经网络,用 Softmax 预测中心词;
网络结构:
输入层:上下文词的 One-Hot 编码:
分布式表示:将词向量从高维稀疏(One-Hot)转换为低维稠密,捕捉语义关联(如 “hotel” 和 “motel” 的向量邻近)。
参数共享:嵌入矩阵
投影层:聚合上下文向量(如求和或平均):
聚合上下文向量(默认平均或求和),忽略词序(“词袋” 特性),生成统一的上下文表示。
输出层:Softmax 计算中心词概率:
训练方法:最小化负对数似然损失(NLL),通过梯度下降更新词向量和网络参数。
优点:
效率优势:CBOW 聚合上下文向量后预测单中心词,计算量低于 Skip-gram(后者需用单中心词预测多个上下文词);
语义平滑:对高频词的向量学习更稳定(如 “the” 的上下文丰富,平均后噪声更低),符合 Word2Vec 对大规模语料的优化目标;
架构简化:舍弃传统神经网络的隐层(对比 NNLM),仅保留 “嵌入 - 聚合 - Softmax” 三层,契合 Word2Vec “快训” 的工程需求。
7.3 LM Basics
定义与目标
概率模型:计算句子出现的概率,即
应用:文本生成、拼写纠正、机器翻译、语音识别等。
数学建模
链式法则:将联合概率分解为条件概率的乘积:
马尔可夫假设:假设当前词仅依赖前
概率估计:传统方法通过计数计算概率,例如
补充:语言模型的评估。除了概率计算,常用困惑度(Perplexity)衡量模型对语料的拟合能力,值越低表示模型越好。
7.4 神经网络语言模型与循环神经网络(RNN)
之前的 Word2Vec 有不少缺陷。如何使用神经网络进行改进?
7.4.1 基本概念
神经网络的改进
词向量平均:将上下文词向量平均后输入 Softmax,但忽略词序(“词袋” 缺陷)。
向量拼接:拼接上下文词向量,但输入长度不固定(无法应对变长输入),参数无法共享。
RNN 的结构与原理
3 层架构:
输入层(Input Layer):接收单个时间步的输入向量
隐藏层(Hidden Layer):核心记忆单元,通过隐藏状态
输出层(Output Layer):根据当前隐藏状态
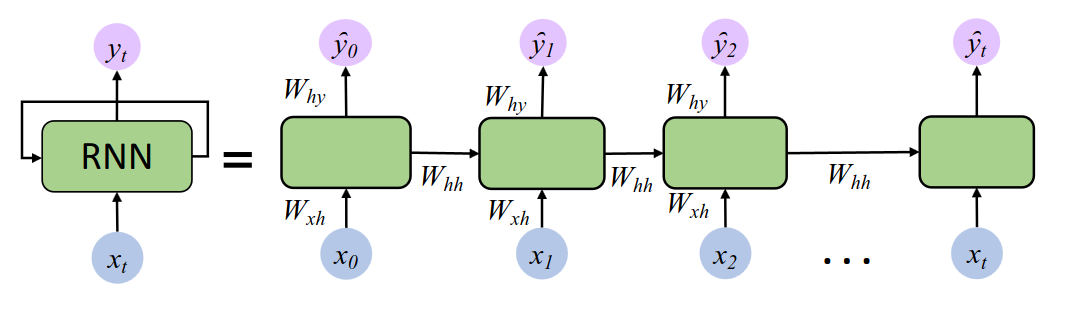
核心参数:
意义:同一组参数在所有时间步复用,大幅减少参数数量,且允许模型学习序列的通用模式。
隐藏状态更新:
历史信息传递:
当前信息输入:
非线性激活:
输出:
理解:每一步的隐藏状态
7.4.2 训练方法
和一般的神经网络一样,借助反向传播计算损失值和整体梯度下降,以此改进模型参数,不过 forward pass 和 backward pass 需要和时间相关,这被称为 Backpropagation Through Time(BPTT)如下图所示:
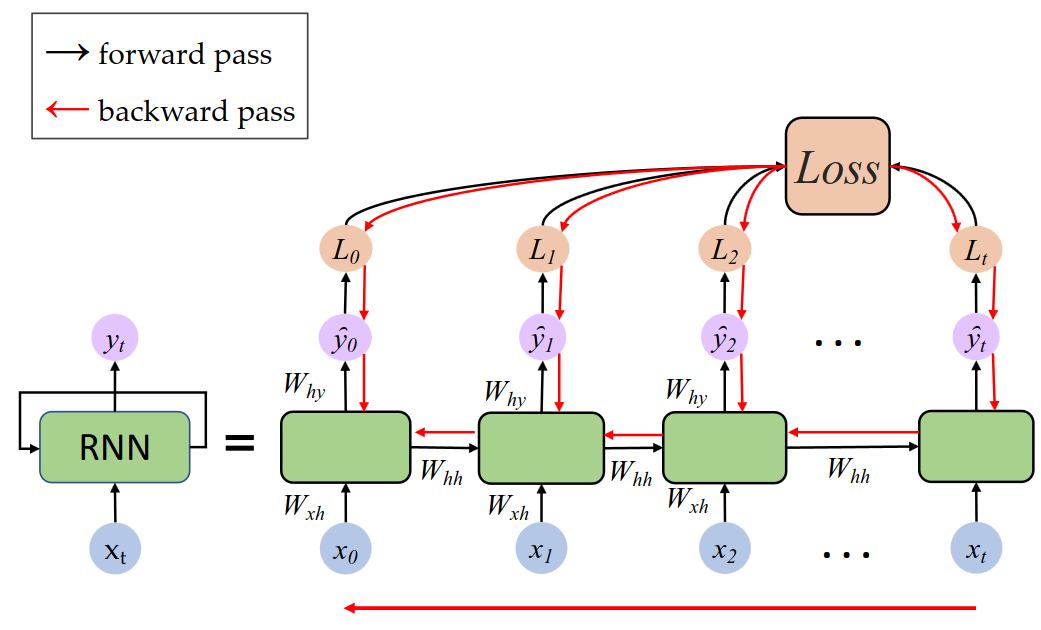
7.4.3 总结
RNN 架构总结:
核心设计:通过隐藏状态
计算图展开:同一组参数(
训练方法:通过 “时间反向传播”(BPTT)计算梯度,更新参数;
应用场景:
序列分类:如情感分析,输入文本序列,输出类别概率(如 “喜欢机器学习”->85% 正面)。
序列生成:
诗歌生成:输入前 n-1 个字符,预测下一个字符(如 “床前明月”->“光”);
音乐生成:根据乐谱序列预测下一个音符至;
机器翻译:通过编码器 - 解码器结构实现语言转换(如中文 “我到了”->英文 “have arrived”)。
RNN 的优势和局限:
优势:
处理可变长序列:通过动态更新隐藏状态,适应任意长度的输入序列,无需固定输入维度。
捕捉序列依赖:理论上可记忆任意历史信息,例如在语音识别中关联前后音素。
局限:
长期依赖问题:标准 RNN 难以捕捉长距离依赖(如句子开头的主语与结尾的谓语),因梯度反向传播时易出现 “梯度消失” 或 “梯度爆炸”。
基于对这点缺陷的改进,后续发展出 LSTM、GRU 等改进结构。
并行计算困难:每个时间步依赖前一步状态,无法像 CNN 一样批量并行处理。
Chapter 8. Transformer & Attention
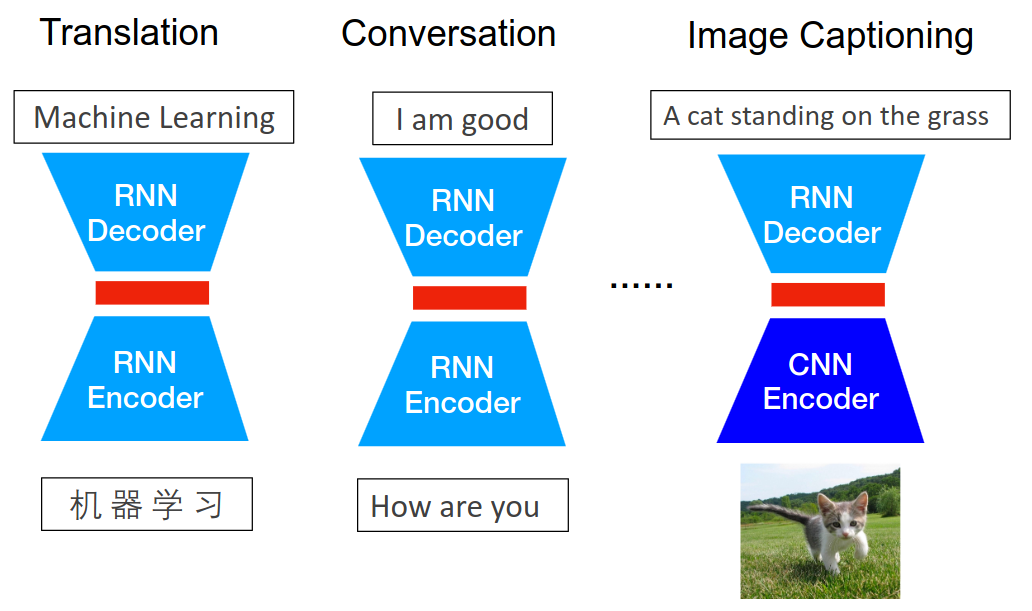
NLP(自然语言处理)核心任务:涵盖机器翻译、情感分析、信息检索、问答系统、文档摘要等序列到序列(Seq2Seq)问题。例如,将 “机器学习” 译为 “Machine Learning”,或根据对话历史生成回复。
8.1 从 RNN Encoder-Decoder 到 Attention 机制
8.1.1 基本概念
RNN Encoder-Decoder 是序列到序列(Seq2Seq)学习的基础模型,其设计核心是解决序列映射问题(如机器翻译、问答生成等)。
它的设计结构如下:
Encoder(编码器):用 RNN 将输入序列
公式:
Decoder(解码器):基于上下文向量
公式:
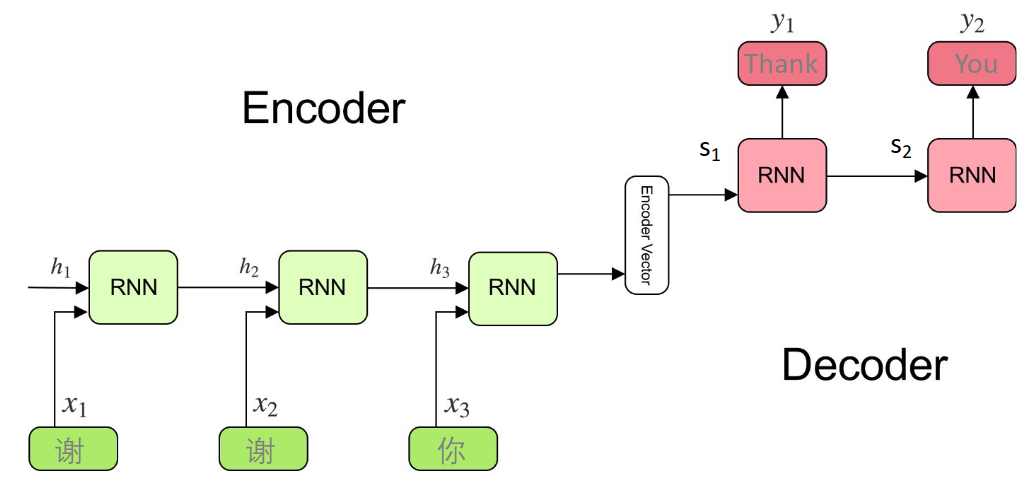
直观理解:以机器翻译为例(如 “我到了”->“have arrived”):
Encoder 将中文 “我到了” 逐词处理,最终用向量
Decoder 基于
8.1.2 训练方法
使用交叉熵作为损失函数。仍然是梯度下降方法对目标函数进行优化。
对于训练数据集
8.1.3 思考与总结
Tip
为什么设计成 Encoder-Decoder 结构?
解决序列映射的通用性需求:自然语言处理中,大量任务(如机器翻译、对话生成、文本摘要)本质是序列到序列的转换。例如:
输入 “如何学习机器学习?”(问题序列),输出 “学习机器学习需要掌握数学基础和编程技能”(回答序列); Encoder-Decoder 通过 “编码 - 解码” 的抽象框架,将这类问题统一为 “输入序列→语义向量→输出序列” 的流程,具有通用性;
利用 RNN 处理序列依赖的能力:RNN 的特点是隐藏状态可捕捉序列中的时间依赖(如前一个词影响后一个词的含义)。Encoder 用 RNN 处理输入序列,将时序信息编码到
固定向量的语义压缩:将变长序列压缩为定长向量
Tip
为什么这种设计是有效的?
数学上的合理性:概率建模
模型通过最大化条件概率
实验验证:机器翻译的突破
2014 年 Cho 等人提出的 Encoder-Decoder 模型,实验数据发现模型能通过
结构上的灵活性
Encoder 和 Decoder 可独立设计:如 Encoder 用双向 RNN 增强语义捕捉,Decoder 用单向 RNN 保证生成顺序。
可扩展为更复杂模型:后续添加 Attention 机制(如文档中提到的动态上下文向量
RNN Encoder-Decoder 的地位和总结:
在 Transformer 出现前,RNN Encoder-Decoder 是处理 Seq2Seq 任务的主流框架,解决了以下具体问题:
机器翻译:实现不同语言之间的序列映射(如中英互译);
语音识别(ASR):将语音信号序列转为文本序列;
对话系统:根据对话历史生成回复(如 “How are you?”->“ I am fine”);
突破传统模型的局限性:相较于早期的统计机器翻译或规则系统,Encoder-Decoder 通过端到端学习(数据驱动而非人工规则)解决了以下痛点:
语义保持:通过 RNN 的隐藏状态捕捉长距离语义依赖,避免传统模型中短语对齐的局限性;
泛化能力:可通过大量数据训练适应不同场景,无需手动编写翻译规则。
为后续技术奠定基础:尽管 RNN Encoder-Decoder 存在长序列信息丢失的问题(如文档中提到的 “当序列变长时性能下降”),但其设计思想为 Attention 机制、Transformer 等后续技术提供了起点。例如:
Attention 机制通过动态计算
Transformer 用 Self-Attention 替代 RNN,彻底解决了序列依赖导致的并行计算限制。
RNN Encoder-Decoder 模型的局限性:
RNN 将整个序列压缩为单一向量
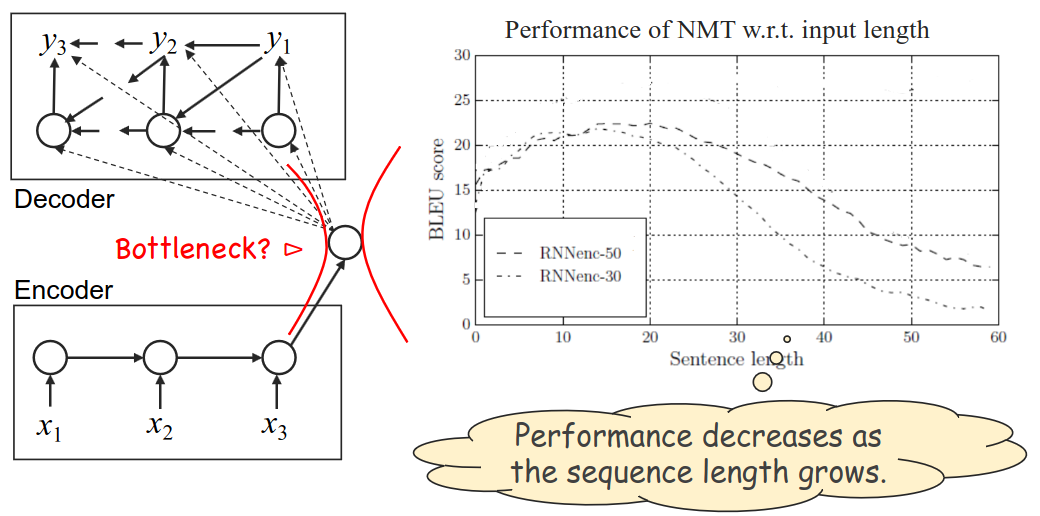
总而言之,RNN Encoder-Decoder 的本质是用 RNN 的序列处理能力实现语义的压缩与重建,其有效性源于对序列任务本质的抽象(语义映射)和数学上的概率建模。尽管存在长序列缺陷,但其 “编码 - 解码” 框架至今仍是许多复杂模型(如 Transformer)的设计基础,推动了 NLP 从规则系统向数据驱动的深度学习转型。
8.1.4 改进:Cross Attention (Encoder-Decoder Attention)
如何克服 RNN Encoder-Decoder 的长序列缺陷?人们曾认为,可以通过动态计算序列上下文压缩向量
它的目标是: 在解码器生成目标序列的第 t 个词时,动态地、有选择性地关注输入序列的所有编码状态(而非原先只关注 Encoder 最后一个隐藏状态),以获取与当前解码步骤最相关的上下文信息。
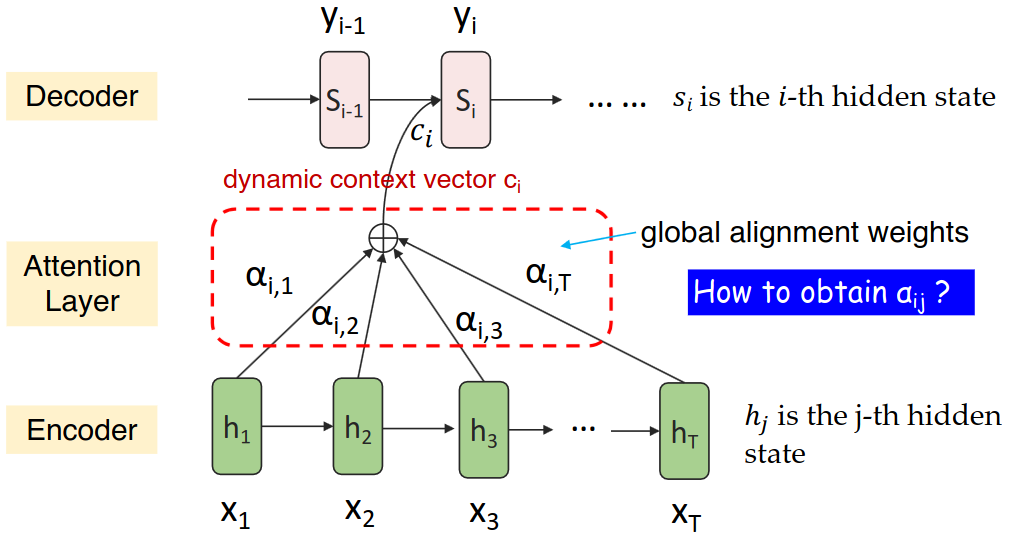
输入:
Encoder 所有时刻的隐藏状态:
Decoder 当前步的隐藏状态
在计算
或者也结合了上一步的注意力上下文
计算过程:
计算对齐分数: 对于输入序列的每一个位置
常用方法:
点积:
加性:
缩放点积:
计算注意力权重: 将对齐分数
权重满足:
动态计算上下文向量: 用注意力权重
整合上下文: 将计算出的上下文向量
concat) 或者相加 (add),形成一个新的、富含输入信息的表示预测输出: 使用
8.2 Self-Attention: Transformer 的核心组件
现在仍然有 RNN Encoder-Decoder With Attention 解决不了的问题,也就是对于多层 RNN 而言,每个位置上的 hidden states 总是要依赖于前一个位置上的 hidden states(回顾 Encoder 和 Decoder 的多层 RNN 结构),这导致模型难以并行计算。
因此人们引入了 self-attention,让每个词同时关注所有词,实现并行计算。例如,处理句子 “The animal didn't cross the street because it was too tired” 时,“it” 可直接关联到 “animal”,无需依赖中间隐藏状态。
self-attention 的目标是: 让序列中的每一个元素(词/Token)都能直接与序列中的所有其他元素(包括它自己)进行交互,计算一个基于“全局”上下文的新的表示。它捕捉的是序列内部的依赖关系。
输入序列的每个元素
Query 向量 (
Key 向量 (
Value 向量 (
投影:
计算过程(对于一个序列而言):
计算注意力分数: 对于序列中的每一个位置
根据 “Attention is all you need” 论文内容,当
(可选) 掩码: 在 Decoder 的 Self-Attention 中,为了避免模型在预测位置
-1e9),这样在 Softmax 后其权重几乎为 0。Encoder 的 Self-Attention 不需要掩码。计算注意力权重: 对每一行
权重满足
计算加权和输出: 对于位置
Tip
核心类比:Q(Query)是 “查询条件”,K(Key)是 “索引标签”,V(Value)是 “存储内容”。三者构成 “检索 - 匹配 - 取值” 的信息处理链,类似数据库通过索引查找数据的过程。
那么多头注意力(Multi-Head Attention)呢?
Transformer 使用它的目的是来增强模型捕捉不同子空间信息的能力:
将
在每个头上独立进行上述 Self-Attention 计算,得到
将
concat) 起来。将拼接后的结果通过一个线性投影层
通俗理解:每个头独立计算注意力,再拼接结果,相当于从不同视角捕捉语义关联。
补充:矩阵运算优化 将
堆叠为矩阵 ,可利用 GPU 加速,通过矩阵乘法并行计算所有注意力权重:
| 场景 | Q 来源 | K/V 来源 | 核心作用 |
|---|---|---|---|
| Cross-Attention | 解码器状态(如 | 编码器输出(如 | 跨序列信息对齐(如翻译中的原文 - 译文映射) |
| Self-Attention | 同一序列的词嵌入 | 同一序列的词嵌入 | 序列内语义关联建模(如 “it” 指代 “animal”) |
| Multi-Head Attention | 分割后的子空间 Query | 分割后的子空间 Key/Value | 多视角捕捉语义(如语法 / 语义并行处理) |
对比:
传统 Attention:解码器生成 “orders” 时,通过
Self-Attention:Transformer 编码器中,“robot” 直接关注 “orders” 的语义关联,无需逐词传递(同序列内)。
位置编码(Positional Encoding)
另外有个小问题:Self-Attention 不感知序列顺序,需额外编码位置信息。
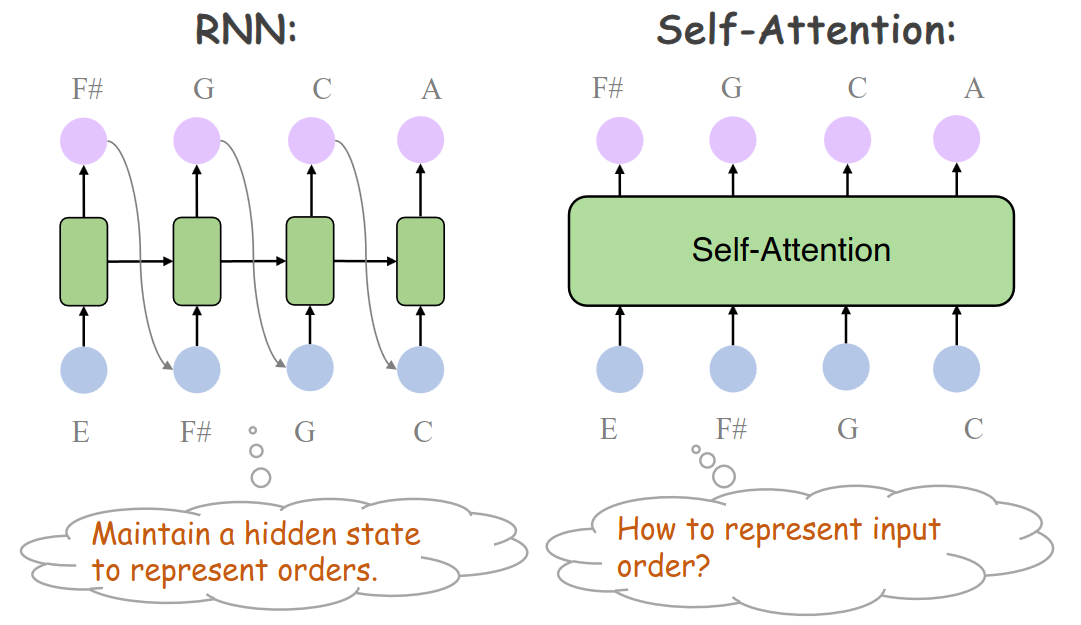
解决方案:为每个位置生成唯一嵌入向量

8.3 Transformer 架构
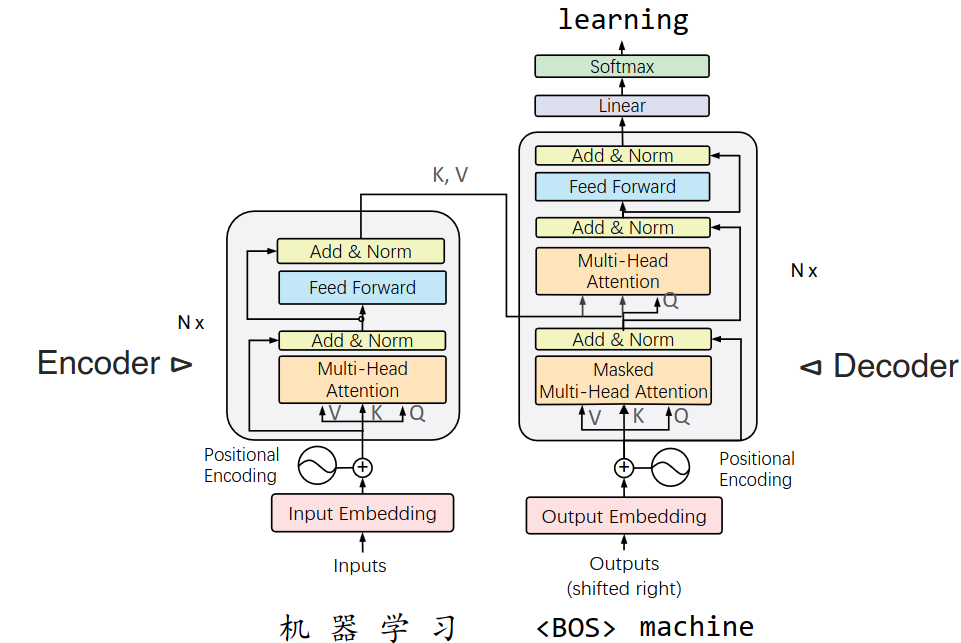
Feed Forward Network(FFN,前馈神经网络),就是两个线性全连接层 + ReLU 激活函数组成的一般神经网络(对每个位置独立处理,增强非线性表达);
Multi-Head Attention 和 Masked 的内容我们前面已经介绍;
训练方法、损失函数、优化算法,与 RNN Encoder-Decoder 完全一致。
8.4 总结
训练流程
数据与损失:与 RNN Encoder-Decoder 相同,使用交叉熵损失优化参数。
并行优势:Self-Attention 的矩阵运算支持批量处理,训练速度远超 RNN。
应用场景
NLP 核心任务:机器翻译(如 Google Translate)、问答系统、文本摘要、对话生成。
跨领域扩展:图像描述(CNN+Transformer)、语音识别、蛋白质序列预测等;
优点
并行计算:彻底摆脱 RNN 的序列依赖,适合长序列和大规模数据至。
长距离依赖:Attention 机制直接建模任意位置的关联,避免 RNN 的梯度消失问题至。
可解释性:注意力权重可视化可解释模型决策(如 “it” 关注 “animal”)。
缺点
计算复杂度:自注意力的时间复杂度为
位置编码局限:固定位置编码对动态时序关系的表达能力有限(后续衍生出相对位置编码)。
数据依赖:依赖大规模标注数据,小数据集下易过拟合。
后续技术演进
预训练模型:BERT(双向 Transformer)、GPT(单向 Transformer)等基于 Transformer 架构,推动 NLP 进入大模型时代。
高效变体:为解决长序列问题,出现了稀疏注意力(如 Longformer、Reformer)、线性注意力(如 Performer)等优化。
总而言之,Transformer 通过 Self-Attention 机制彻底重构了序列建模方式,其核心贡献在于:
摒弃循环结构,实现全并行计算,推动 NLP 模型效率飞跃;
用注意力机制显式建模全局依赖,突破 RNN 的长序列瓶颈;
统一的架构设计为跨领域任务(如语言、视觉、语音)提供了通用框架。
Chapter 9. Large Language Model (LLM)
LLM 的核心目标
构建统一向量空间表示所有文本,实现跨语言、跨任务的知识迁移。
核心路径:通过大规模无监督预训练(如书籍、维基百科数据)获取通用知识,再针对具体任务微调。
预训练与微调的比较参见 9.2;
9.1 预训练语言模型:从 BERT 到 GPT
9.1.1 BERT: Bidirectional Encoder Representations from Transformers
BERT 架构特点
基于 Transformer Encoder,输入序列通过多层自注意力机制生成上下文相关的词向量和句子向量。
首个 token 为
[CLS](分类标记),用于聚合整个句子的语义。
也就是说,它是一个满足下列条件的 Transformer Encoder:
可以学习单词和句子的不同表示。
在大型文本库上进行预训练,然后在小型特定任务数据集(如分类、质量保证)上进行微调;
再次强调:BERT 完全基于 Transformer 模型的 Encoder(编码器) 部分构建。Transformer 由 Encoder 和 Decoder 堆叠而成,BERT 只使用了 Encoder 堆叠。
预训练任务
掩码语言模型(MLM):随机掩盖 15% 的输入 token,让模型预测被掩盖的词,学习上下文依赖。
下一句预测(NSP):判断句子 B 是否是句子 A 的下一句(估计可能性),提升文本连贯性理解。
微调应用场景
句子分类:如情感分析、文档分类,直接使用
[CLS]向量输出类别。词标记:如槽填充(Slot Filling),为每个词分配标签(如时间、地点)。
句子对分类:如自然语言推理,判断假设与前提的逻辑关系。
问答系统(QA):定位文档中问题的答案区间,输出起始位置(s, e)。
补充知识
优点:双向编码能捕捉上下文双向依赖,在理解类任务(如问答、推理)中表现优异。
双向上下文: 对词义消歧、指代消解等任务效果显著提升。
通用性强: 预训练好的模型通过微调,在广泛的 NLP 任务上都能取得当时(2018年)最先进的性能,包括文本分类、命名实体识别、问答、自然语言推理等。
特征丰富: 不同层的输出可以捕捉不同层级的语言信息(语法、语义等)。
缺点:预训练中的 NSP 任务被后续研究发现收益有限,且生成能力较弱(因非自回归架构)。
总结:BERT 是一个基于 Transformer Encoder 堆叠的预训练语言模型。它通过 MLM 任务实现了深度双向的上下文理解,并通过 NSP 任务学习句子间关系。预训练后的模型通过简单的微调即可在多种 NLP 任务上取得优异表现。
9.1.2 自回归架构
什么是自回归架构?
自回归模型的核心在于其序列生成的方式。它假设序列中的每个元素(例如文本中的一个词)都依赖于它之前生成的所有元素。
工作原理:
顺序生成: 模型一次生成序列中的一个 token(词或子词)。
依赖历史: 在生成第
t个 token 时,模型只能访问它之前已经生成的 token(1, 2, ..., t-1)作为上下文信息。它无法利用“未来”的 token(第t+1,t+2, ... 个 token)。概率建模: 模型学习的是整个序列的联合概率分布
P(x1, x2, ..., xT)。这个联合概率被分解为一系列条件概率的乘积:P(x1, x2, ..., xT) = P(x1) * P(x2|x1) * P(x3|x1, x2) * ... * P(xT|x1, x2, ..., xT-1)模型的核心任务就是学习这些条件概率P(xt | x1, ..., xt-1)。
架构基础: 现代 NLP 中的自回归模型几乎都基于 Transformer 的 Decoder(解码器) 部分构建。Transformer Decoder 的特点:
掩码自注意力: 这是实现自回归的关键!在计算第
t个位置的注意力时,会屏蔽(Mask)掉位置t之后的所有位置。这样,第t个位置的表示只能基于1到t-1位置的 token 计算而来,确保在生成时无法看到未来信息。编码器-解码器注意力: 在 Seq2Seq 任务(如机器翻译)中,Decoder 还会关注 Encoder 的输出(源序列的表示)。
同样包含位置编码、前馈神经网络、残差连接和层归一化。
训练目标: 自回归模型的训练目标通常是最大似然估计。给定一个真实的序列 (x1, x2, ..., xT),模型的目标是最大化其自身预测的条件概率的乘积(或等价地,最小化负对数似然)。具体来说,在训练时:
输入是序列的开始标记
[SOS]或整个序列(x1, x2, ..., xT-1)(需要向右移位)。模型被训练来预测序列中的下一个 token
(x2, x3, ..., xT)。
应用场景: 自回归架构天生适合文本生成任务,因为文本生成就是一个从左到右、逐个 token 预测的过程。典型应用包括:
机器翻译
文本摘要
对话生成 (聊天机器人)
创意写作 (诗歌、故事、代码)
无条件文本生成
关键特性:
单向性: 本质上是单向的(通常是左到右),生成当前 token 时只依赖历史。
生成能力强: 非常擅长生成流畅、连贯的文本。
易于并行训练: 在训练时,由于真实的下一个 token 是已知的,可以通过掩码操作实现整个序列的并行计算(预测下一个词的任务可以同时进行)。
推理串行: 在推理/生成时,由于下一个词的输入依赖于前一个词的输出,这个过程是串行的,无法完全并行,导致生成速度相对较慢。
总结自回归架构: 自回归架构是一种序列建模和生成的方法。它假设序列元素按顺序生成,每个元素严格依赖其之前的所有元素。在现代 NLP 中,它主要通过带掩码自注意力的 Transformer Decoder 实现。这种架构是生成式任务(如 GPT 系列)的首选,其训练目标是预测下一个 token(语言模型任务),训练可并行但推理生成是串行的。
9.1.3 GPT: Generative Pre-Trained Transformer
架构与预训练
基于 Transformer Decoder,采用自回归方式预测下一个 token,输入需向右移位(mask 未来信息)。
训练目标:最大化条件概率
p(x_t | x_1, ..., x_{t-1}),即给定前文预测下一个词。
补充知识
GPT 的涌现能力:当参数超过 1000 亿时,模型会突现之前小规模模型不具备的能力,如逻辑推理、数学解题。
应用场景:文本生成(如写作、代码生成)、对话系统(如 ChatGPT)、少样本学习(通过示例快速适应新任务)。
比较:
| 模型 | 架构 | 预训练任务 | 核心能力 |
|---|---|---|---|
| BERT | 编码器 | MLM + NSP | 文本理解 |
| GPT | 解码器 | 自回归语言模型 | 文本生成 |
9.2 微调 Fine-Tuning
9.2.1 微调的核心逻辑
两阶段流程
预训练:在海量无标注数据上学习通用知识。
微调:在小样本标注数据上针对具体任务优化。
全量微调的挑战
计算成本高:全参数微调需大量 GPU 资源(如 GPT-3 微调可能消耗数百万美元)。
过拟合风险:小样本下易过度拟合特定任务,损害模型泛化能力。
9.2.2 参数高效微调(PEFT)技术
Prompt Tuning(提示微调)
在输入前添加可训练的伪 token(Prompt),冻结预训练参数,仅优化提示嵌入。
优势:无需修改模型主体,存储成本极低(仅需训练少量提示参数)。
LoRA(低秩适应)
通过低秩分解将权重更新分解为两个小矩阵,仅训练新增的小矩阵参数。
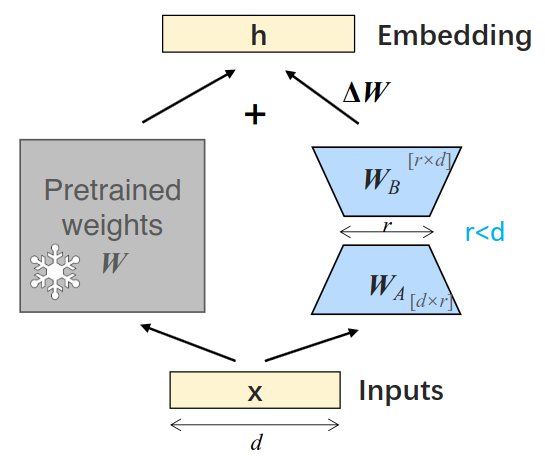
例如:原权重矩阵维度 d×d,分解为 d×r 和 r×d(r<<d),大幅减少可训练参数。
补充知识
其他 PEFT 技术:QLoRA(量化 + LoRA)、Adapter Tuning(添加适配器模块)等,均旨在减少微调成本。
应用场景:企业定制模型(如医疗、法律领域)时,无需全量训练即可适配特定任务。
9.3 提示工程(Prompt Engineering):解锁 LLM 的关键
1. 基础提示技巧
零样本提示(Zero-Shot Prompting)
直接输入任务描述,模型无需示例即可响应。
例:“将文本分类为中性、负面或正面:‘这部电影是我同类中最喜欢的之一’”。
少样本提示(Few-Shot Prompting)
提供少量任务示例,模型通过模仿示例完成新查询。
In-Context Learning: Learning by mimicking demonstration examples in the input context.
例:“review:‘美味的食物’→正面;review:‘食物很糟糕’→负面;review:‘糟糕的菜肴’→?”。
2. 进阶推理提示
思维链(Chain-of-Thought, CoT)
要求模型逐步展示推理过程,提升复杂问题的解决能力。
例:“罗杰有 5 个网球,买了 2 罐,每罐 3 个,现在有多少?→步骤:5 + 2×3 = 11”。
ReAct 框架(推理 + 动作)
模型生成推理轨迹,并调用外部工具(如搜索)获取信息,再整合回答。
例:查询 “苹果遥控器最初设计控制什么程序”→模型搜索发现是 Front Row 媒体中心。
补充知识
提示工程的关键原则:清晰任务描述、提供示例、结构化输出格式(如 JSON),可显著提升模型响应准确性。
挑战:提示脆弱性(微小措辞变化可能导致结果差异),需通过提示优化(如自动搜索最佳提示)缓解。
9.4 检索增强生成(RAG):弥补 LLM 知识局限
1. RAG 的核心逻辑
问题:LLM 无法获取最新或领域特定知识(如 2025 年的事件),回答可能 “幻觉”。
解决方案:通过检索外部文档,将相关知识注入提示,辅助 LLM 生成准确回答。
2. RAG 架构三要素(Framework)
嵌入模型:将文本转换为向量(如 BERT 生成句嵌入)。
向量数据库:存储文档向量,支持快速检索(如 FAISS、Chroma)。
LLM:结合检索到的文档生成回答。
3. 工作流程(Pipeline)
索引阶段:将文档分块,生成向量存入数据库。
检索阶段:查询转换为向量,匹配最相关的文档块。
生成阶段:将检索结果加入提示,LLM 基于上下文回答。
补充知识
RAG 的应用:企业客服(基于内部知识库)、实时新闻问答、学术文献检索等。
优化方向:文档分块策略(如基于语义分块而非固定长度)、检索结果重排序(提升相关性)。
Chapter 10. CNN & CV
CNN 和一般的神经网络比较:
像素序列: 破坏了图像的空间结构;
对位置不敏感:关注整个图像而不是局部特征;
平移变体:对特征的全局位置敏感;
太多参数:全连接层产生大量参数。
参见另一份笔记。
案例补充:
AlexNet:

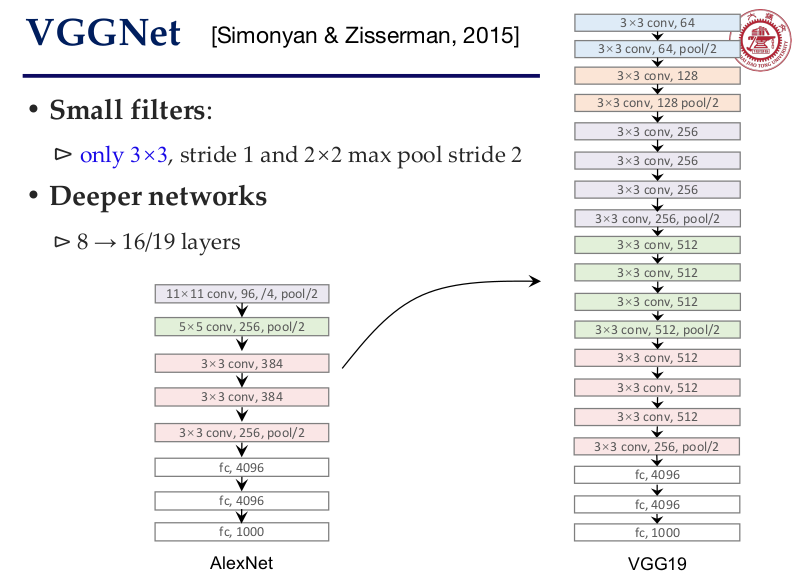
注意到,为什么使用小的 Kernels(filters)?
3 个 3x3 步长为 1 的卷积层与 1 个 7x7 的卷积层的感受野效果相同;
但是往往更深一点能带来更多的 non-linearities;
并且 3 个 3x3 相较于 1 个 7x7 可以有更少的参数量;
网络一定越深越好吗?事实上不一定,过深的网络也会导致表现较差。假说:the problem is an optimization problem, deeper models are harder to optimize;
更深的优化案例:ResNet
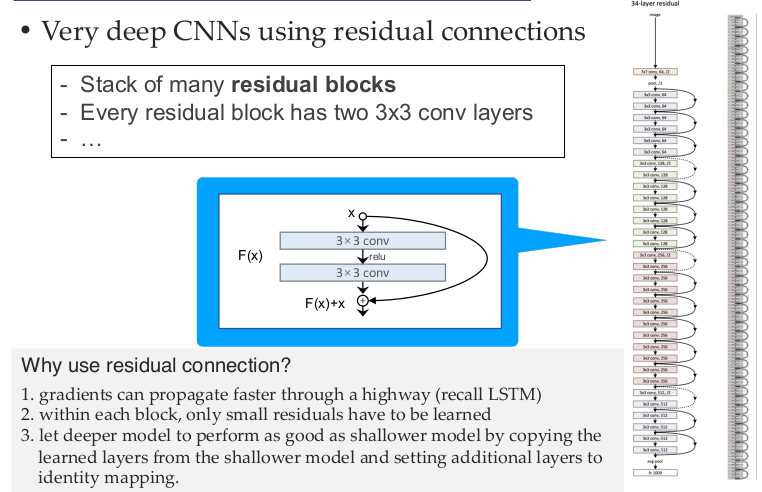
为什么用残差连接?
梯度的传播速度更快(回顾 LSTM);
在每个区块内,只需学习较小的残差;
通过复制较浅模型的学习层,并设置附加层进行特征映射,让较深模型的性能与较浅模型一样好;
Chapter 11. Computer Vision
计算机视觉的 5 大任务:
图像分类(Image Classification)
目标:将整幅图像归为单一类别(如 “猫”“狗”)。
技术路径:卷积神经网络(CNN)+ 全连接层(MLP)+ Softmax 分类器,损失函数采用交叉熵(Cross-Entropy)。
扩展:实际应用中需考虑类别不均衡(如稀有物种识别)、域适应(不同拍摄场景迁移)等问题。
语义分割(Semantic Segmentation)
目标:对图像中每个像素标注语义类别(如 “草地”“猫”“树”),不区分同类物体个体。
应用场景:自动驾驶道路分割、医学影像病灶检测。
目标检测(Object Detection)
目标:定位图像中多个物体的边界框(Bounding Box)并分类。
与分类的区别:增加坐标回归(x, y, w, h)任务。
图像字幕生成(Image Captioning)
目标:生成描述图像内容的自然语言句子(如 “A cat standing on the grass”)。
跨模态特性:融合视觉理解与语言生成。
图像生成(Image Generation)
目标:从噪声、文本等输入生成真实图像,PPT 中仅简略提及。
扩展:近年扩散模型(Diffusion Models)如 Stable Diffusion 已成为主流,相比早期 GAN 更易控制生成质量。
11.1 语义分割
核心挑战与朴素思路
直接对每个像素独立分类不可行,因缺乏上下文信息(如单个像素无法判断是 “猫毛” 还是 “草地”)。
滑动窗口法:用 CNN 提取图像块特征,预测中心像素类别,但重叠块特征重复计算,效率极低。
全卷积网络(Fully Convolutional Networks, FCN)
架构创新:
去掉传统 CNN 的全连接层,仅用卷积层实现端到端像素级预测。
引入下采样(池化 / 步长卷积)和上采样(反卷积 / 转置卷积),平衡语义信息(高层)与空间细节(低层)。
问题:原始分辨率下卷积计算量极大,需通过多尺度特征融合优化。
U-Net:编码器 - 解码器的经典范式
结构特点:
编码器(左半部分)下采样提取语义特征,解码器(右半部分)上采样恢复空间分辨率。
跳跃连接(Skip Connections)直接传递低层空间信息,解决 FCN 中细节丢失问题。
应用:生物医学图像分割(如细胞边界提取),因对小目标(如微小病灶)检测效果优异。
扩展:后续出现的 DeepLab 系列引入空洞卷积(Atrous Convolution),在不降低分辨率的前提下扩大感受野。
11.2 目标检测
对于 single object 而言,就是 Classification + Localization;
但是对于 multiple objects 而言,问题是 each image (CNN) needs a different number of outputs!
简单的想法是,枚举图像的不同裁剪,应用 CNN 将每个裁剪分类为对象或背景。
还有问题:需要对大量位置、比例和长宽比应用 CNN,计算成本非常高!
11.2.1 两阶段检测:R-CNN 系列的演进
R-CNN(2014):
流程:选择性搜索(Selective Search)生成约 2000 个区域提议→每个区域缩放到固定尺寸→CNN 提取特征→SVM 分类 + 边界框回归。
缺点:单张图像需 2000 次 CNN 前向传播,速度极慢(49 秒 / 图)。
Fast R-CNN(2015):
优化:先对整图提取特征,再在特征图上裁剪区域,避免重复计算。
引入 ROI Pooling(感兴趣区域池化)统一不同尺寸区域的特征维度。
Faster R-CNN(2015):
核心创新:嵌入区域提议网络(RPN),用 CNN 直接生成提议框,替代传统选择性搜索。
锚框(Anchor Box)机制:在特征图每个点预设不同尺寸、比例的锚框,预测其是否为物体及坐标偏移。
速度提升:从 R-CNN 的 49 秒 / 图到 Faster R-CNN 的 0.2 秒 / 图。
11.2.2 端到端检测:YOLO(You Only Look Once)
核心思想:将图像划分为 S×S 网格,每个网格预测 B 个边界框及其置信度,同时输出 C 类概率。(将目标检测形式化为回归问题)
优势:单阶段直接回归,速度可达实时(30FPS+),适合安防监控、自动驾驶等场景。
局限性:对小物体检测效果差(如远处行人),因网格划分粗粒度丢失细节。
扩展:后续 YOLOv2-v8 通过锚框聚类、特征金字塔网络(FPN)等优化,平衡速度与精度。
11.2.3 图像字幕生成:从编码器 - 解码器到注意力机制
基础框架:编码器 - 解码器(Encoder-Decoder)
编码器:CNN(如 ResNet)提取图像特征。
解码器:循环神经网络(RNN/LSTM)生成文本,初始隐藏状态为图像全局特征 c。
问题:全局特征 c 难以捕捉图像局部细节(如 “猫” 的位置),导致描述模糊。
引入注意力机制(Attention Mechanism)
核心改进:让解码器在生成每个词时,动态关注图像特定区域。
数学原理:
计算解码器隐藏状态与图像各区域特征的相关性得分
用 Softmax 生成注意力权重
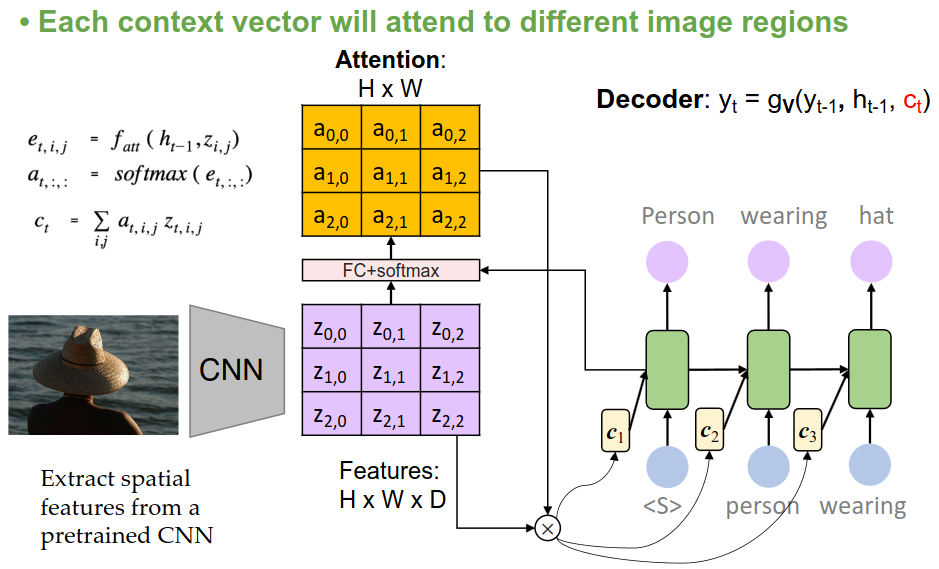
效果:生成更精准的描述(如 “一只坐在草地上的黑猫”),代表工作为 Xu 等人的 “Show, Attend and Tell”。
Transformer 的应用
扔掉 CNN,直接上 Transformers,端到端地学!
Vision Transformer(ViT):
将图像分块(如 16×16 像素),通过线性投影转化为序列,结合位置编码输入 Transformer 编码器。
在大规模数据(如 ImageNet-21K)预训练后,性能超越传统 CNN(如 ResNet)。
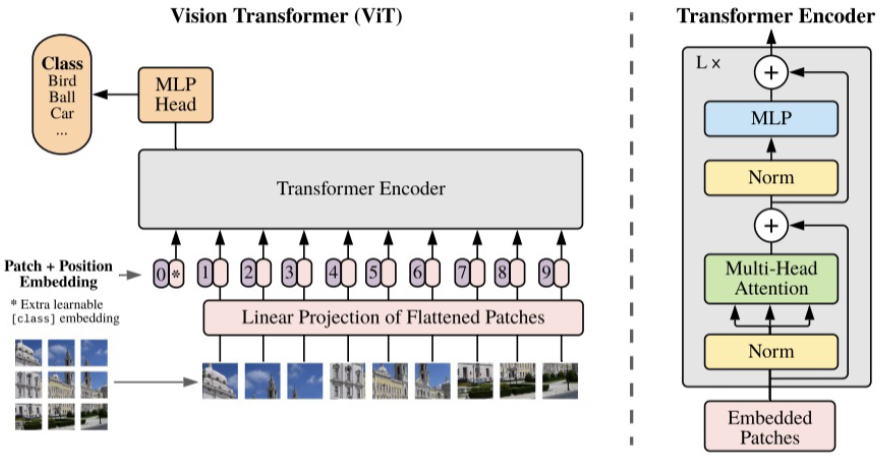
DETR(Detection Transformer):用 Transformer 直接预测目标边界框,无需锚框,实现端到端检测。
11.2.4 视觉语言模型(VLMs):多模态融合的前沿
CLIP(Contrastive Language-Image Pretraining)
核心思想:通过对比学习,将图像和文本映射到同一嵌入空间,使语义相近的图像 - 文本对在空间中距离更近。
零样本学习能力:训练时不接触具体任务标签,推理时通过文本提示(如 “A photo of a dog”)实现目标检测、分类。
LLaVA:大语言模型与视觉的结合
架构:
视觉编码器:CLIP 或 ViT 提取图像特征。
语言模型:基于 LLaMa,将视觉特征投影后与文本嵌入拼接,实现多模态理解。
应用:视觉问答(如 “图中猫的品种是什么”)、图像描述生成,支持双语(中英)交互。
其他 VLMs:
| 模型 | 特点 |
|---|---|
| CogVLM | 支持图像接地(定位文本提及的物体)和对话交互 |
| Qwen-VL | 零样本目标检测能力,图像分辨率 448×448 |
| PaLM-E | 具身智能(Embodied AI),结合视觉与机器人控制,可规划抓取动作 |
11.2.5 扩展知识
实例分割(Instance Segmentation):
目标:既标注像素类别,又区分同类物体个体(如分割出图像中所有猫,并编号)。
代表模型:Mask R-CNN(在 Faster R-CNN 基础上增加掩码预测分支)。
三维视觉:
如深度估计、点云分割,在自动驾驶(激光雷达)和 AR/VR 中至关重要,PPT 未涉及但属于 CV 前沿领域。
无监督学习在 CV 中的应用:
PPT 最后提及 K-means、VAE 等,但未展开。近年自监督学习(如 SimCLR、MoCo)通过对比学习从未标注图像中提取特征,已成为预训练主流。
11.2.6 总结:计算机视觉的演进脉络
从 CNN 到 Transformer,从单模态到多模态,CV 技术始终围绕 “如何更高效地理解视觉世界” 发展。未来趋势将聚焦于:
多模态融合:视觉与语言、音频、传感器数据的深度结合(如具身智能)。
无监督 / 自监督学习:降低对大规模标注数据的依赖。
实时性与轻量化:边缘设备(如手机、机器人)上的高效推理。
通用智能:从单一任务(如图像分类)到通用视觉理解,向人类级视觉认知靠近。
Chapter 12. 无监督学习
大致有几个类别:
Clustering: Learn hidden structures
K-means
Gaussion Mixture
Generative: density estimation
GAN
VAE
Diffusion
Dimensional Reduction: Learning data compression
Principal component analysis
Auto-encoder
无监督学习 vs 监督学习:
监督学习:目标是发现数据属性与目标标签的关联(如根据特征预测房价)。
无监督学习:数据无目标标签,旨在挖掘隐藏模式(如将用户按行为分群)。
12.1 Clustering & K-Means
12.1.1 基本定义
聚类是无监督学习的典型任务,其定义为:将无标签数据组织成相似的组(簇),簇内数据 “相似”,簇间数据 “相异”。
核心问题:如何定义 “相似” 与 “相异”?通常用距离度量,如欧氏距离(L2 距离)。
簇的表示:每个簇用 “质心”(Centroid)表示,即簇内所有数据点的均值向量。
与其他实例相比,中心点必须与所代表集群中的实例更为相似。
一个簇内的实例与同一簇的中心点比与其他簇的中心点更相似。
12.1.2 K-means 算法的原理与步骤
K-means 是最经典的聚类算法之一,其目标是将数据划分为 K 个簇,使簇内平方和(SSE)最小。
算法核心步骤
初始化质心:随机选择 K 个数据点作为初始簇中心。
分配数据点:对每个数据点,计算其到所有质心的 L2 距离,分配到最近的簇。
更新质心:根据当前簇分配,重新计算每个簇的质心(均值)。
质心公式:
迭代收敛:重复步骤 2-3,直到质心不再显著变化或 SSE 收敛。
收敛条件
数据点不再重新分配到其他簇;
质心位置变化极小;
簇内平方和(SSE)的减少量低于阈值。
SSE 公式:
12.1.3 K-means 的关键问题与优化
时间复杂度:设计算两点间距离复杂度为
单次迭代:分配簇需计算
优化方向:使用 mini-batch 加速,或采用近似距离计算。
局部最优与初始质心敏感性
问题:K-means 保证收敛到局部最优,但不一定是全局最优,且结果依赖初始质心选择。
找到全局最优是 NP-Hard 问题。
解决方案:选取更好、heuristic 的初始质心;
k-means++ 算法:
随机选第一个质心;
后续质心按与已选质心的距离平方加权概率选择(距离越远,选中概率越高);
确保质心分布更均匀,减少局部最优风险。
什么导致了 K-Means 算法的不确定性?
初始质心选择的随机性:算法初始质心(种子点)的随机选择会直接影响最终聚类结果。不同的初始质心可能导致算法收敛到不同的局部最优解,甚至出现收敛缓慢或簇结构次优的情况。例如,若初始质心集中在数据的某一区域,可能导致簇划分失衡。
算法本身只能收敛到局部最优:k-means 算法的优化目标(最小化簇内平方和)属于 NP 难问题,理论上无法保证找到全局最优解,只能收敛到局部最优。这种特性使得结果对初始条件敏感,不同运行过程可能产生不同的聚类结构。
K 值预先指定的主观性:用户需要手动指定簇的数量 K,但真实数据的最佳簇数往往未知。错误的 K 值会导致聚类结果偏离数据的真实结构,例如 K 过大可能分裂合理簇,K 过小可能合并不同类别的数据。
如何选择簇数 K?
肘部法则(Elbow Method):计算不同 K 值对应的簇内平方和(WSS),当 WSS 下降趋势变缓(“肘部”)时的 K 为最优解。
WSS 公式:
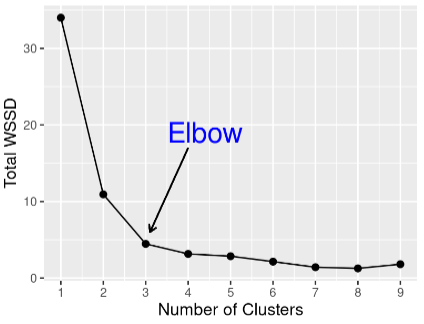
12.1.4 K-means 的优缺点与应用场景
优点
简单高效:原理直观,实现容易,时间复杂度接近线性,适合大规模数据。
广泛适用:是最常用的聚类算法之一,适用于数值型数据。
缺点
假设限制:假设簇为球形,无法处理不规则形状(如月牙形簇)。
参数依赖:需预先指定 K 值,且对离群点敏感(均值易受极端值影响)。
数据要求:必须定义 “均值”,无法直接处理分类变量(需先编码)。
典型应用
图像分割与压缩:将像素值聚类,用质心颜色代表簇内像素,减少颜色数量(如将 256 色压缩为 32 色)。
客户分群:根据消费行为将用户分组,制定精准营销策略。
文档聚类:将相似主题的文档归为一类,辅助信息检索。
12.1.5 K-means 与其他聚类算法的对比
与层次聚类的区别: K-means 是 “划分聚类”(直接分 K 簇),层次聚类是 “树状聚类”(自底向上或自顶向下构建簇层次)。
与 DBSCAN 的区别: DBSCAN 基于密度(可发现任意形状簇,能识别离群点),而 K-means 基于距离(假设球形簇)。
适用场景建议:
数据呈球形分布、维度较低时,优先选 K-means;
数据形状复杂、存在离群点时,考虑 DBSCAN 或高斯混合模型。
12.2 Dimensionality Reduction
降维的核心问题:“除了数据聚类,是否存在其他数据模式”。降维试图通过挖掘 “隐藏特征” 来简化高维数据。
12.2.1 背景:维度灾难(The Curse of Dimensionality)
理论挑战
高维空间中,数据稀疏性导致泛化所需数据量呈指数增长。
例子:若有
实际痛点
数据内在维度可能更低(如 3D 物体的图像本质是 2D);
高维特征导致计算开销大(内存、时间);
难以可视化和解释高维数据。
降维的定义:减少数据维度(属性数),同时保留数据的内在特征,找到决定数据特性的 “隐藏维度”。
直观示例:3D 数据可投影到最佳 2D 或 1D 空间,保留主要变化趋势。
12.2.2 线性降维算法:PCA 主成分分析
除了 PCA,线性降维算法还有:Linear discriminate analysis (LDA)、Factor analysis 等等;
核心思想:找到方差最大的投影方向(主成分),使降维后数据信息损失最小。
数学推导
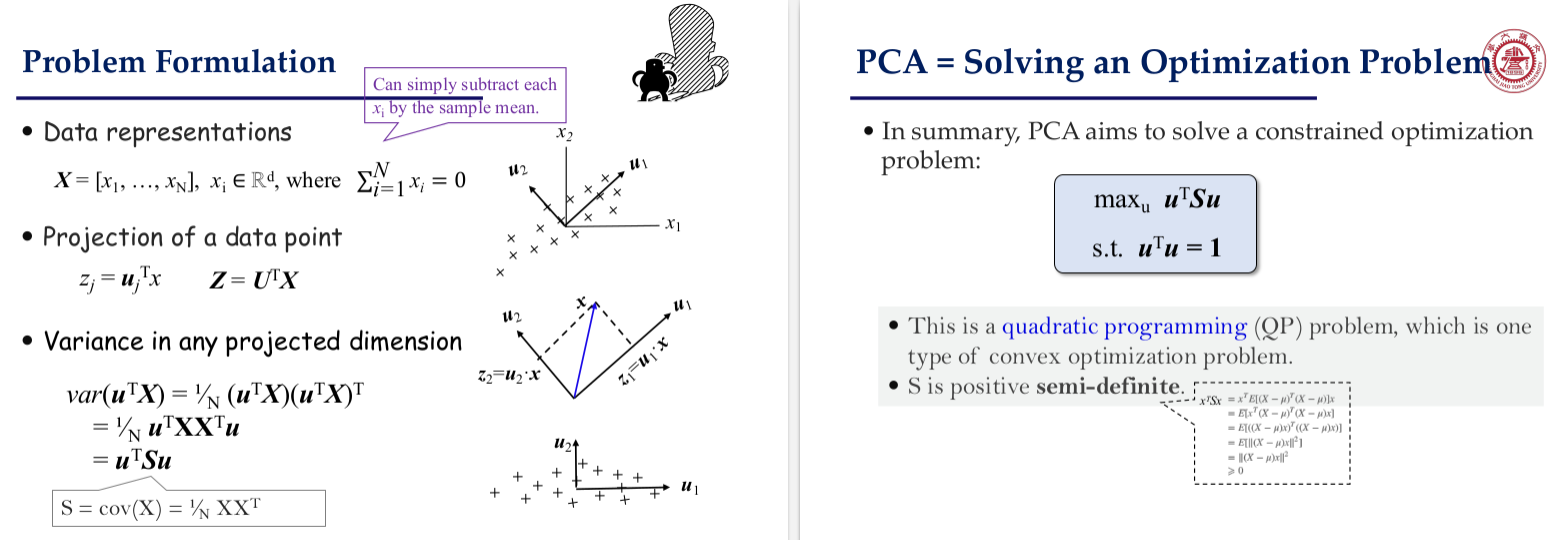
优化问题:最大化投影方差
求解:通过特征值分解,主成分对应协方差矩阵的特征向量,特征值大小代表方差贡献。
降维步骤:
数据中心化(平均值归 0);
计算协方差矩阵;
特征分解,按特征值排序;
选择前 k 个特征向量构成投影矩阵。

主成分数量
基于信息损失公式:
应用案例:
特征脸(Eigen-Faces):将人脸图像(如 24×24=576 维)降维到低维空间,用前 k 个主成分表示人脸特征。
数据可视化与压缩:如手写数字图像的降维表示。
PCA 的优缺点
优点:计算高效、无参数、可解释性强(主成分有明确物理意义);
缺点:假设线性关系,对噪声和离群点敏感,可能丢失非线性结构。
为什么说 PCA 可以看成神经网络?
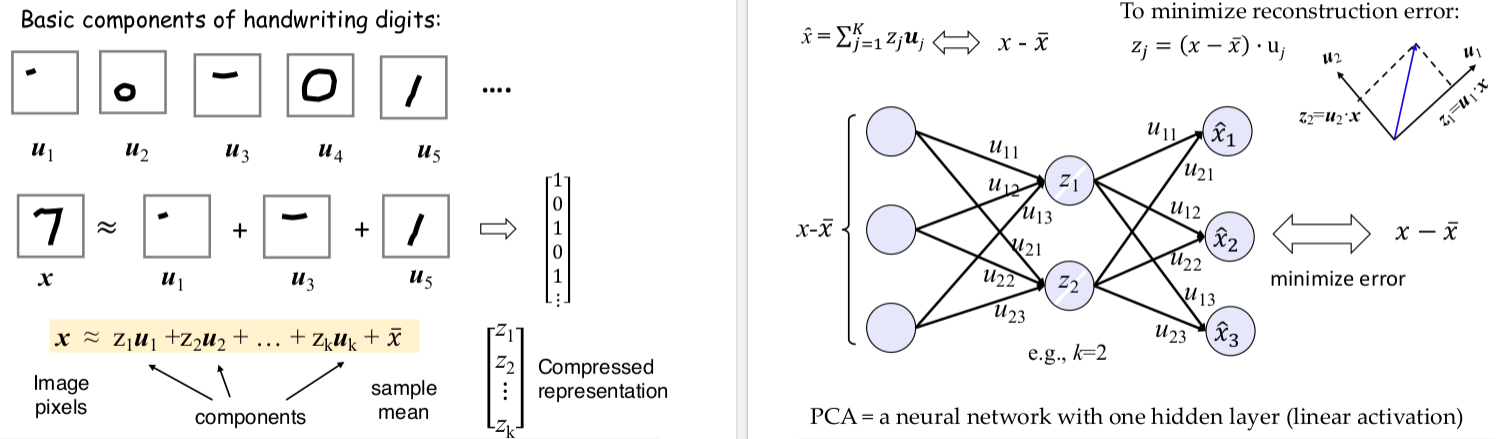
12.2.3 非线性降维:自动编码器(Auto-encoder)
除了 Auto-encoder,非线性降维算法还有:KPCA, KLDA、Multidimensional scaling (MDS)、t-SNE 等等;
KPCA(核 PCA):通过核函数将数据映射到高维,再用 PCA 降维,处理非线性关系;
t-SNE:将高维数据映射到 2D/3D,保持局部相似性,常用于可视化;
多维缩放(MDS):保持数据点间距离关系,用于可视化。
基本结构
由编码器(Encoder)和解码器(Decoder)组成,通过训练使输出重构输入,学习低维表示 z。
数学表达:
与 PCA 的联系(与上一节 “为什么说 PCA 可以看成神经网络?” 连起来看)
线性自动编码器(激活函数为线性)等价于 PCA,此时隐藏层权重对应 PCA 的特征向量。
扩展:深度自动编码器
通过多层网络捕捉非线性关系,瓶颈层(Latent Layer)强制学习压缩表示。
应用:
降噪(Denoising Auto-encoder):输入含噪声数据,输出干净数据,用于去噪;
图像压缩(如 U-Net):结合卷积结构,平衡压缩率与重构质量。
对比总结:
| 方法 | 线性 / 非线性 | 监督性 | 核心优势 | 典型应用 |
|---|---|---|---|---|
| PCA | 线性 | 无监督 | 计算高效、可解释性强 | 图像压缩、数据预处理 |
| 自动编码器 | 非线性 | 无监督 | 灵活处理非线性、可定制网络结构 | 图像去噪、特征学习 |
| t-SNE | 非线性 | 无监督 | 优秀的高维数据可视化能力 | 单细胞数据可视化、图像检索 |
| LDA(线性判别分析) | 线性 | 有监督 | 利用标签信息,注重分类区分性 | 人脸识别、文本分类 |
12.2.4 降维算法的延伸与前沿
生成模型与降维的结合
降维可视为生成模型的预处理步骤,如 VAE 通过隐变量空间(低维)生成新数据;
Diffusion 模型通过逐步去噪学习数据分布,本质上是高维到低维(噪声空间)的映射逆过程。
实际挑战
如何平衡维度压缩与信息保留;
非线性降维方法的计算复杂度较高;
高维数据中 “有效特征” 与 “噪声” 的区分。
12.3 深度生成网络
生成模型的本质:通过建模数据分布
12.3.1 生成对抗网络(GAN)
核心原理:生成器与判别器的对抗训练
生成器(G):将随机噪声(如高斯分布)转换为伪造数据,目标是让伪造数据接近真实分布
判别器(D):区分真实数据与伪造数据,目标是最大化判别准确率。
对抗目标函数:
其中,生成器试图最小化 V(让判别器误判),判别器试图最大化 V(提高辨别力)。

典型架构与变种
DCGAN(深度卷积 GAN):用卷积层替代全连接层,提升图像生成质量,支持潜在向量的算术运算(如 “戴眼镜男性” 向量 - “男性” 向量 + “女性” 向量 = “戴眼镜女性”)。
条件 GAN(Conditional GAN):引入标签条件(如文本、类别),控制生成内容,例如将语义标签转为街景图像。
CycleGAN:解决无配对数据的域转换问题(如照片转油画),通过双向生成器(A->B 和 B->A)和循环一致性损失确保转换合理性。
应用与局限
应用:图像风格转换、人脸生成、视频深度伪造、医学图像合成。
局限:训练不稳定(易出现模式崩溃)、缺乏显式概率分布、难以控制生成细节。
12.3.2 变分自编码器(VAE):概率视角下的生成与压缩
核心思想:潜码的概率约束
编码器(Encoder):将图像 x 编码为潜码 z,假设 z 服从高斯分布
解码器(Decoder):从 z 还原图像,目标是最大化对数似然
前项为重构损失(确保生成图像与原图相似),后项为正则化项(确保潜空间连续可采样)。
为什么要正则化?正则化后有什么性质?
连续性:潜空间中相近的点->解码后内容相似;
完整性:从潜空间取样->解码后总是 “有意义 ”的内容;
总结:
优势:潜空间具有语义连续性(如调整某一维度可控制人脸表情),适合数据压缩与生成。
局限:
生成图像常模糊(因概率分布假设),难以捕捉高分辨率细节;
潜码 z 的大小与原始图像不同(小得多);
内容是一次性生成的。
12.3.3 扩散模型(Diffusion Models):从噪声到真实的逆向生成
双向过程:前向扩散与反向去噪
前向扩散(固定过程):逐步向图像添加高斯噪声,直至变为纯噪声
其中
反向去噪(训练过程):通过神经网络从噪声

模型架构与算法
常用 U-Net 架构,结合残差块和自注意力机制,处理多尺度特征。
训练算法:随机采样噪声并添加到图像,优化去噪网络;
采样算法:从纯噪声开始,逐步去噪生成图像。
突破与挑战
优势:生成质量超越 GAN(如 ImageNet 高分辨率合成),模型设计灵活(可结合文本、图像条件)。
挑战:推理速度慢(需数十至数百步),计算资源消耗大,近年通过快速采样算法(如 DDIM、PLMS)逐步优化。
对比:
| 模型 | 核心机制 | 生成质量 | 训练难度 | 典型应用 |
|---|---|---|---|---|
| GAN | 对抗博弈 | 高(清晰) | 高(易崩溃) | 图像生成、深度伪造 |
| VAE | 变分推断与潜码约束 | 中(模糊) | 低 | 数据压缩、特征提取 |
| Diffusion | 渐进去噪 | 极高 | 中 | 高分辨率图像、文本生成 |
Chapter 13. 强化学习
13.1 机器学习分类与强化学习定位
机器学习三大范式对比
监督学习:基于带标签数据(x,y)学习映射x->y,目标是预测具体标签,例如图像分类(“这是苹果”)、回归分析等。
无监督学习:处理无标签数据x,学习数据内在结构,例如聚类(“这个和那个相似”)、降维等。
强化学习:核心是 “智能体与环境交互”,通过状态 - 动作对和奖励信号,学习最大化长期奖励的策略,例如机器人控制、游戏 AI 等。
强化学习的独特性
数据类型:非独立同分布(状态转移具有时序依赖)。
学习目标:优化长期累积奖励,而非即时预测准确性。
典型场景:Atari 游戏(如打砖块)、AlphaGo、自动驾驶等。
13.2 强化学习基础框架:马尔可夫决策过程(MDP)
13.2.1 核心概念
MDP 的数学定义
五元组
S:状态空间(如游戏画面、机器人位置)。
A:动作空间(如上下左右移动)。
P:状态转移概率
R:奖励函数
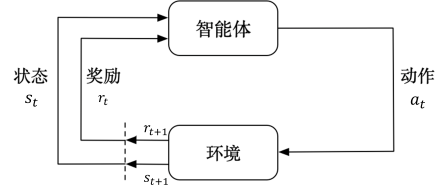
目标:学习一种能使长期收益最大化的政策(即状态-行动映射)。
MDP 的动态过程
智能体从状态
环境反馈奖励
重复上述过程,形成轨迹
长期回报定义为
核心问题:策略与值函数
策略
Q 函数(动作值函数):
最优策略:
13.2.2 值函数方法 (Value Learning):Q-learning 与深度 Q 网络(DQN)
Q-learning 算法核心
表格法:直接存储所有状态 - 动作对的 Q 值,通过迭代更新:
案例演示:在 “格子世界” 中,智能体通过不断试错更新 Q 表,最终找到最优路径(如从起点到 + 1 奖励格,避开 - 1 惩罚格)。
如何估计 Q-Score?
Monte-Carlo: Use Real Return;
Time-Difference: Use the value from the next state;

DQN:解决维度灾难的突破
核心创新:用深度神经网络(如 CNN)近似 Q 函数
关键技巧:
经验回放:存储历史轨迹
目标网络:使用固定参数的 “目标网络” 计算目标 Q 值,缓解训练不稳定。
网络结构:输入状态(如图像),输出各动作的 Q 值。
训练目标:最小化 MSE 损失

应用:在 Atari 游戏中,DQN 通过图像输入直接学习控制策略,如打砖块游戏中自动决策跳跃时机。
13.2.3 策略梯度方法 (Policy Learning):直接优化行为策略
策略梯度的核心思想
与值函数的区别:不通过 Q 值间接推导策略,而是直接用神经网络参数化策略
优化目标:最大化期望回报
梯度公式:
REINFORCE 算法(策略梯度的经典实现)
采样轨迹
对每个动作
沿梯度方向更新参数:
策略梯度的优缺点
优点:适合连续动作空间(如机器人关节角度控制),可学习随机策略。
缺点:样本效率低,需要大量轨迹才能收敛,且可能陷入局部最优。
13.2.4 案例解析:AlphaGo 的混合智能框架
AlphaGo 的核心组件
策略网络(Policy Network):预测落子位置的概率p(a∣s),减少搜索空间。
价值网络(Value Network):评估棋盘状态的胜负概率V(s),替代蒙特卡洛树搜索的随机模拟。
蒙特卡洛树搜索(MCTS):结合策略网络的先验概率和价值网络的评估,选择最优落子。
训练流程
监督学习阶段:用人类专家棋谱训练策略网络,准确率达 57%。
强化学习阶段:通过自我对弈优化策略,胜率提升至 80%,并训练价值网络评估状态。
MCTS 集成:策略网络缩小搜索范围,价值网络评估节点价值,实现 “精准搜索”。
意义与扩展
突破点:解决了围棋的巨大状态空间问题(约10700种局面),证明 RL 在复杂博弈中的可行性。
进化:AlphaGo Zero 进一步抛弃人类数据,完全通过自我对弈从零学习,超越之前所有版本。
13.2.5 强化学习在自然语言处理中的应用
序列生成:SeqGAN 与对话系统
问题:传统监督学习(如 Teacher-forcing)生成的文本可能缺乏多样性或逻辑性(如重复回答 “I don't know”)。
RL 方案:
状态:编码器隐藏状态 + 已生成的文本序列。
动作:生成下一个词。
奖励:结合 BLEU、ROUGE 等指标,或自定义奖励(如避免单调回答、促进信息流动)。
大语言模型优化:RLHF(人类反馈强化学习)
三步流程:
监督微调(SFT):用人类标注的(prompt, response)对微调 LLM。
奖励模型(RM):训练模型预测人类对不同回答的偏好排名。
RL 优化:用 PPO 算法基于 RM 的奖励信号进一步微调 LLM,使其输出更符合人类预期。
作用:解决 LLM “胡说八道”“社会偏见” 等问题,如 ChatGPT 通过 RLHF 提升对话安全性和相关性。
| 概念 | 定义 / 特点 | 应用场景 |
|---|---|---|
| 监督学习 | 基于标签数据学习映射 | 图像分类、回归 |
| 无监督学习 | 学习无标签数据的内在结构 | 聚类、降维 |
| 强化学习 | 通过交互学习最大化长期奖励的策略 | 游戏 AI、机器人控制 |
| Q-learning | 用表格存储 Q 值,迭代更新 | 小状态空间问题(格子世界) |
| DQN | 用神经网络近似 Q 函数,解决维度灾难 | Atari 游戏、图像控制 |
| 策略梯度 | 直接优化策略的概率分布 | 连续动作空间(机器人) |
| AlphaGo | 策略网络 + 价值网络 + MCTS 的混合框架 | 围棋博弈 |
| RLHF | 用人类反馈微调 LLM,提升回答质量 | 对话系统(如 ChatGPT) |
强化学习的挑战与扩展(补充知识点)
核心挑战
样本效率低:RL 需大量交互数据,尤其在真实环境中成本高昂(如机器人训练)。
探索 - 利用权衡:智能体需平衡 “探索新动作” 与 “利用已知高回报动作”。
稳定性问题:参数更新可能导致策略崩塌,如 DQN 中的目标网络即为缓解该问题。
前沿方向
多智能体 RL:研究智能体在竞争或合作环境中的学习,如星际争霸 AI AlphaStar。
离线 RL(Off-Policy RL):利用历史数据训练,无需在线交互,适合医疗、金融等敏感领域。
分层 RL:将复杂任务分解为子任务,提升学习效率,如机器人分阶段完成组装任务。
应用扩展
推荐系统:根据用户反馈动态调整推荐策略,提升点击率和留存率。
资源管理:数据中心服务器调度、通信网络带宽分配等。
医疗决策:制定个性化治疗方案,优化用药顺序和剂量。