Deep Learning

References: EECS 498.008 / 598.008 Deep Learning for Computer Vision;
Deep LearningImage ClassificationFirst Classifier: Nearest NeighborImprovementsHyper-parametersUniversal ApproximationSummaryLecture 2. Linear Classifier2.1 Definition2.2 Views & Shortcomings2.0 数学知识回顾2.0.1 The Definition for Entropy2.0.2 Joint Entropy & Conditional Entropy2.0.3 Cross Entropy & Relative Entropy (KL Divergence)2.0.4 Mutual Information2.3 Choose the Parameter
Image Classification
图像分类是计算机视觉要解决的核心问题之一。不过有一些问题:
Semantic Gap;
Viewpoint Variation(像素改变巨大)
Intraclass Variation(组内不同个体的差距巨大)
Fine-Grained Categories(更细的分类力度);
Background Clutter(不同的背景造成影响);
Illumination Changes(环境光照);
Deformation(不常见的变形);
Occlusion(图像遮挡);
但图像识别能作为其他图像处理任务的基石,例如:
Object Detection(图像检测可以通过移动图像窗口来实现);
Image Captioning(看图说话,可以通过图像识别总结出主题词汇,再根据分类选择词汇组成句子);
实现方法:
def detect(image): # do calculations here ... return label不像一般算法,没法直接编码计算的代码;
尝试:使用边缘提取算法,然后按照轮廓特征来判断?例如识别一只猫,就判断近三角形的耳朵、胡须如何分布等等。
这些做法将人类经验硬编码,不是个好选择;
可能边缘提取算法错误(无法提取?)、可能有些猫不准确长这样(Fine-Grained/Deformation)?
即便我们找到所有 corner cases,第二天如果想识别银河系,又该怎么做(泛化性)?
于是引入机器学习:Data-Driven Approach;
收集一组图像和标签;
使用机器学习算法训练分类器;
在新的图像上评估这个分类器;
xdef train(images, labels): # do statistical stuff return model
def predict(model, test_images): # use model to predict labels return test_labels
常见数据集是 MNIST(识别 28x28 灰度图片中的 0~9 手写数字,50K 用于训练,10K 用于测试),被称为 “CV 界的黑腹果蝇”,它很简单,但不能证明算法的优秀性;
还有一个常见数据集是 CIFAR-10(识别 10 类 32x32 RGB 图片,从生物到非生物 50K 训练、每类 5K,以及 10K 测试、每类 1K),虽然量小但难度大于 MNIST;以及 CIFAR-100,数据量和 CIFAR-10 一样,但有 100 类,其中 20 个超类每个里面有 5 个细分的类别。
还有一个图片分类的 “金标准” 是 ImageNet 数据集,包含 1000 类图片,约 1.3M 训练集、50K 验证集、100K 测试集。其中测试指标为 Top 5 Accuracy(算法预测可能性前 5 的 labels 必须有一个是正确的);
还有一些特殊的数据集针对某些特殊需求,例如 MIT Places 针对的是场景识别;而 Omnigot 则要求算法以尽量少的数据集得到尽可能精准的模型(1623 类图片,每类只有 20 张),这被称为 “low-shot classification problem”(小样本分类问题);
First Classifier: Nearest Neighbor
先来个最简单的算法(甚至不配叫深度学习算法):最近邻。
trainphase 直接记录所有训练数据;predictphase 将输入数据与所有训练数据逐个比较,确定最近的图片对应的 label;定义两个图片距离:
Manhattan Distance(曼哈顿距离):
Minkowski Distance(闵氏距离):
相似度(如余弦相似度):
算法描述:
选取邻居数
对测试集中的每个需要被分类的样本
按距离数据排序,取最近的
这个方法有致命缺陷:训练
此外,使用曼哈顿距离并不是很聪明(只是把看起来相近的图片归为一类,例如白色背景的猫和白色背景的青蛙会被归成一类)。
我们引入 decision boundaries(决策边界)来描述,这幅图被称为 Voronoi Tessellation(维诺图,沃罗诺伊分割):
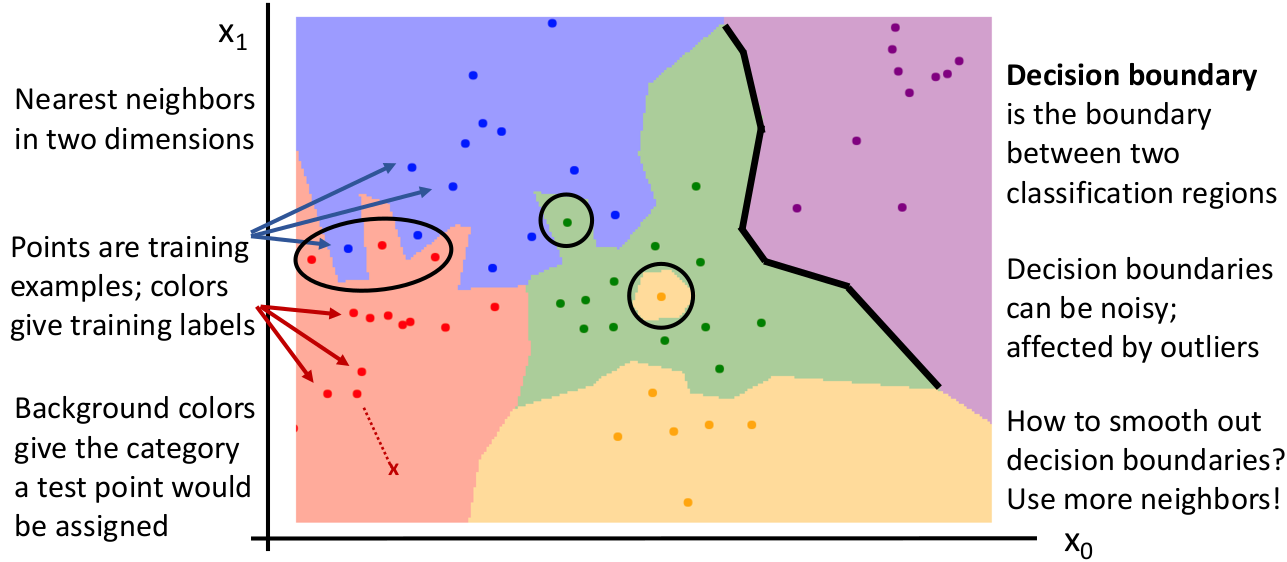
对于一个二维数据(例如 2 个像素的图像),点代表训练集,颜色代表标注的 labels。没有标注点的是其他的可能数据。而黑线就是按照模型算法判断的决策边界。所谓区分两个类型就是确定两个类的决策边界(黑线)。下次测试输入数据时查看落在哪块区域内即可。
某些异常情况(例如噪点)可能导致真实的分类边界参差不齐。
Improvements
改进 1:为了解决最近邻不准确的问题(直接使用最近邻居的 label),我们引申出 K-Nearest Neighbor(KNN),从 K 个最近邻居中选出得票最多的 label 作为测试数据的 label。这个改进我们可以从决策边界图看到:
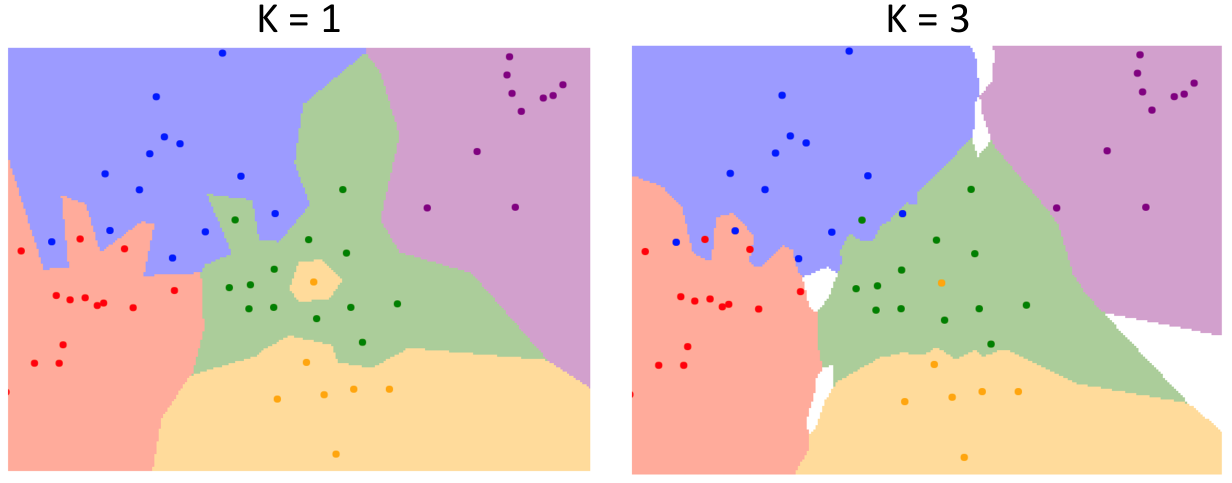
可以看到,这使得模型的决策边界变得平滑,并且减小了测试数据受到个别噪声点的影响。
但 K-Nearest Neighbor 的问题是可能存在投票平局的问题,此时在图中显示是空白的颜色。你可以使用 heuristics(例如 fall back 到一个的情况)。
总结:
K 过小:算法效率提升,但更易受到噪声点的影响;
K 过大:算法效率不高,且包含太多其他类的 votes,over-smoothing 分类结果,模型效果不佳;
改进 2:更改 Distance Metrics。在 KNN 的基础上,我们将判断图像相似度的距离指标从曼哈顿距离(
曼哈顿距离的边界都是由垂直或水平或 45 度倾角的线段组成;而欧几里得距离的边界虽然还是由线段组成,但是可以朝向任意方向(相当于用计算量换取更灵活准确的分类方式)。
这里虽然看不出来二者的优势究竟在哪,但是这告诉我们一个好消息:对于任何一个数据类型,只要给一个 distance matrics,就能将 KNN 算法应用上去!例如衡量两个 PDF 文件的相似性(作为 distance),可以使用 TF-IDF(Term Frequency-Inverse Document Frequency,词频-逆文件频率)similarity,它通常被用在一些 NLP 应用中。
TF-IDF 指出,字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降。
前者因为它更能代表一篇文章的主题,后者因为它更有可能是停用词、或者是不能很好作出区分的词汇。
这再次证明了,不考虑性能的情况下,调整 KNN 的距离指标计算方法可以在不同的应用场景下获得很好的分类效果。
Hyper-parameters
另一方面,除了 training data,还有一类参数例如 邻居数 K、最佳的距离指标(各种距离还是其他算法?),它们被称为学习算法的 “超参数”(hyper-parameters),意指在训练前就应该为学习算法确定的(而不是训练时获得),能对算法的运作方式产生间接深远影响的参数。
通常情况下,超参数的最优取法与具体问题有关,没有 silver bullet;有几种做法:
做法 1:使用全部数据作为 training data,并选对自己训练的数据集而言 accuracy 最大(最佳)的超参数;
这是不行的。以 KNN 为例,我们会永远选择 K=1 的情况,因为总是和训练集数据自身比;
做法 2:将数据分为
training和test,使用training来训练,但选择对test而言 accuracy 最大的超参数;使用机器学习的目标之一就是要 generalize 到未知的数据,因此这么做是更合理的。
但这也是不行的,和上一条一样是有问题的。这会导致对你的模型表现的错误预估。
因为这不是单纯的 evaluate,而是设置超参数。这么做会导致模型仍然会被所谓的 “unseen data” 的知识所污染(你还是参考了 unseen data 来对算法的超参数作出了决定),模型和上面的一样,不能对真正未知的数据有足够的泛化性。
做法 3:将数据分为
training、validation和test,使用training来训练、validation来确定最优超参数,test来做最终一次的 evaluation;这条是真正比较科学的做法。不过还有更科学的做法。
做法 4:cross-validation;将数据分为 N 个
fold,以及一个test,遍历每个 fold,将每个 fold 作为一次validation set,然后除了它和test的剩余部分做training,如此得到 N 个不同的最佳超参数,然后根据某种策略(如最大 accuracy / 超参数平均值等)选取最好的超参数。理论上这条比上一条更好,但是需要的计算量也更大。
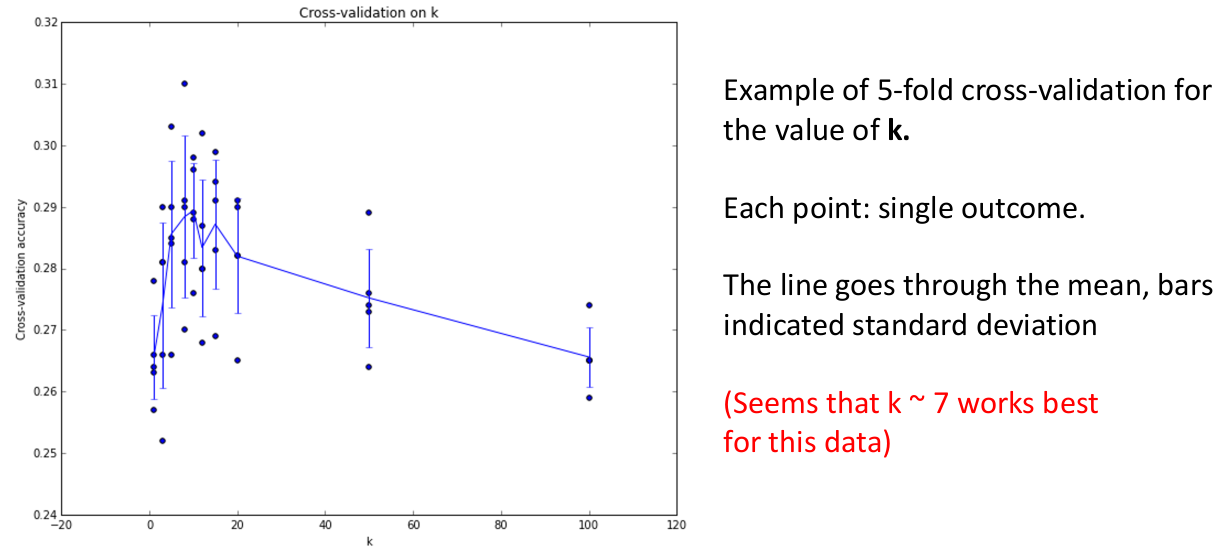
如上图是 5-fold cross validation 模式训练的 KNN 模型在超参数
Universal Approximation
由于 KNN 对于处理的函数几乎没有做前提假设,因此在训练集大到接近无穷时,KNN 甚至可以表示几乎任何常见的函数(有点像泰勒级数的逼近)。
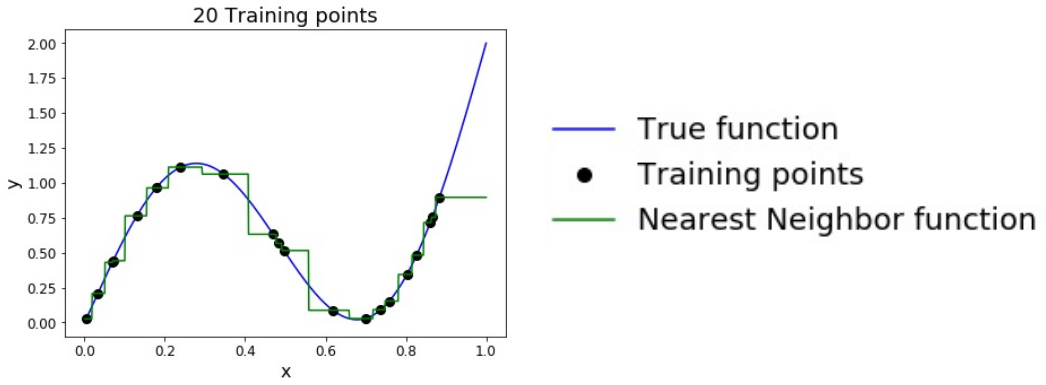
问题是随着维度的增加,需要逼近真实解到同样程度的训练集大小会呈指数级增加,这被称为 “curse of dimensionality”(维度诅咒)。这是不可接受的,因为上面图的情况仅仅是一维的数据。如果是一张 32x32 的图片,训练集大小的数量级会在
正因如此,KNN 在 raw pixels 的图像处理领域很少被用到,总结:
需要大量数据来达到不错的效果(维度诅咒);
distance metrics 在图像领域并不具有明显语义;
但某些情况下(不是 raw pixels)KNN 能很好的识别图像特征,例如在深度卷积神经网络计算得到的特征向量(特征提取)中进行 KNN 并以此做图像分类/看图说话等等,可以得到很好的效果(从容应对 various viewpoints、bg clutter、illumination changes 等干扰因素),这个后面讨论。
Summary
优势:
容易理解、实现;
新数据可以直接添加到训练完的模型上,几乎不会损害模型精度、不需要从头训练;
劣势:
测试/推理性能极差,显然不能 scale 到大规模数据上(尤其是计算距离非常耗时);
维度诅咒;
空间占用大;
数据一般需要标准化后再传入;
Lecture 2. Linear Classifier
2.1 Definition
线性分类器实际上是一种参数化方法(Parametric Approach),使用这种方法的分类器被称为 Parametric Classifier。考虑对图像进行分类的实质:
输入一个
MxNxC大小的图片(C为图像的通道),视作一个矩阵;通过函数
得到一个
参数分类器将成为学习神经网络方法的基础。本节将正式介绍最简单的 parametric classifier pipeline 实例:线性分类器。
首先给出线性分类器的运算方法:定义
对图像矩阵
线性分类器还有一个特点:我们先忽略 bias 部分,
,这告诉我们即便对图像乘以固定的 scale 也会影响最后的 score。但是实际上对图像所有像素乘以 scale 从人眼来看只是改变了图像的饱和度,并不影响辨认它的结果。(bug or feature?) 这个特点是否对效果有重要影响,取决于损失函数的选取,我们后面讨论。
现在我们从 3 个角度来理解这个分类器,并且从中感性地分析出它的缺点。
2.2 Views & Shortcomings
我们从线性代数的角度理解,实际上是将权重矩阵的每一行与输入图像的 flatten vector 分别内积并添加 bias。
从视觉角度理解,其实会发现
但同时我们从 template vector 中可以发现,实际上虽然我们想要做的是识别某个物体,但模型仍然对输入图像的细节、周边的 context 这些 evidence 关注较多(而不仅仅是图片中的物体本身),这可能会出现 “过拟合” 的嫌疑。
例如你将棕色的汽车放在草原中图片交给线性分类器,它很有可能会认为图中的物体是一头鹿。
线性分类器还有一个问题是同一个类型的不同模式的识别,例如训练数据中 “马” 类图片中马的不同朝向、“车” 类图片的不同颜色。主要原因是线性分类器对每个类只准备了一个 template,没有办法 disentangle 这些不同的模式(导致 template vector 将同一类型的不同模式的特征糅合在一起);
我们再考虑新的角度:代数几何的角度。我们对图中的任意一个像素,例如
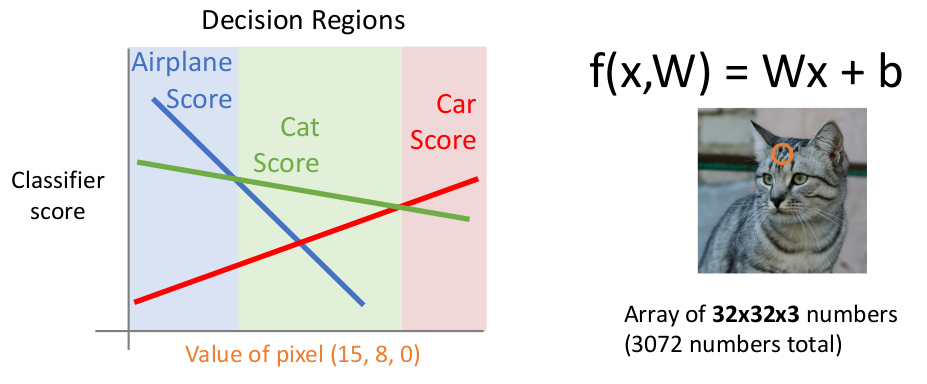
现在考虑扩展一下 “视野”,引入另一个像素,例如
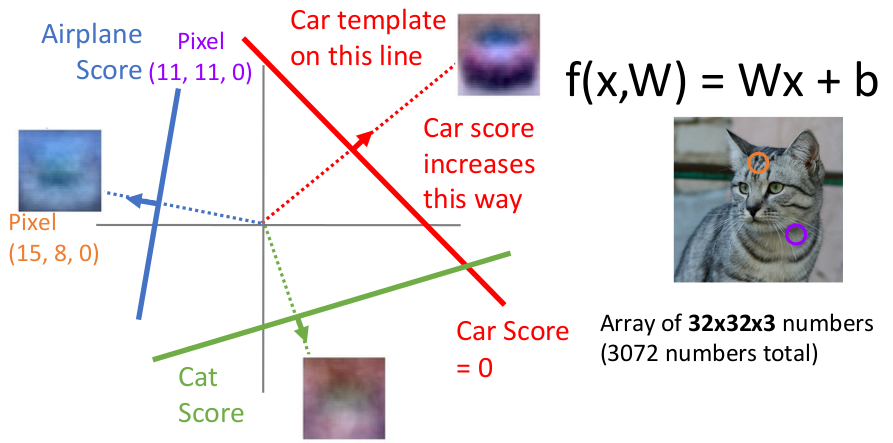
所以在几何的角度上,线性分类器就是使用多个超平面(hyper-plane)分割欧式超空间上的样本点。
但这个方法只能在低维上用作启发,因为高维度上的空间我们无法想象和理解,它是反直觉的。
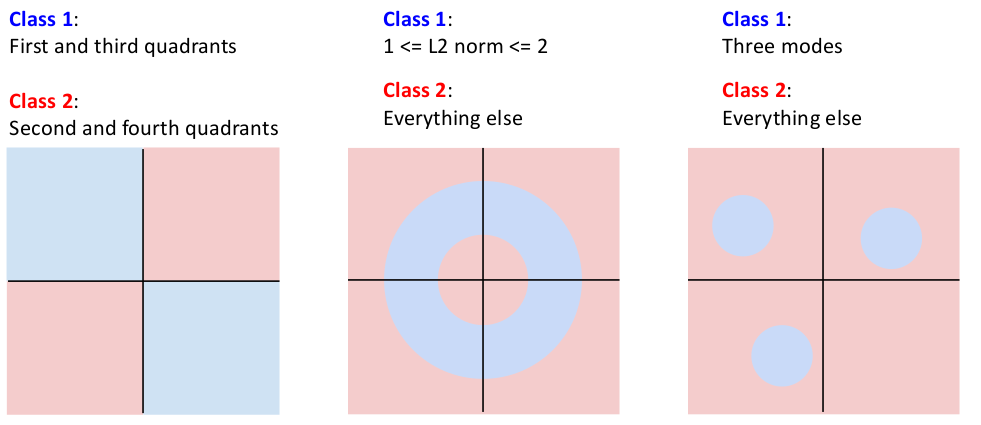
在几何的角度,我们又能分析出来线性分类器对于某些特定的数据类型没法很好地分类:
(从二维上看)分布在对角象限内的类型数据。(不可能用线性超平面完美切分)
在欧式超空间中,一类数据分布为离散的不同聚簇中。(不可能用线性超平面完美划分)这恰好可以对应前面我们说 “同一类别的不同模式”,例如马的不同朝向;
在欧式超空间中,以半径为特征分布的类型。(不可能用线性超平面完美划分)
它们在数学上有个统一的名称:线性不可分(non-linear separable)。
类似地,我们回忆一下历史上第一个机器学习算法(感知机 perceptron),我们发现这个 perceptron 的数学模型就是线性分类器!
它的重要缺陷就是没法学习 XOR(异或)的数据关系,原因我们可以在二维图像上画出来,验证了之前我们在几何上的结论:
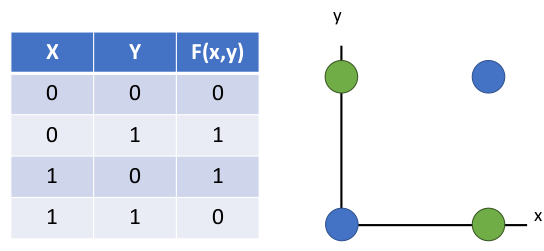
2.0 数学知识回顾
2.0.1 The Definition for Entropy
香农(Shannon)认为,一个事件的不确定性(或者称 surprisal / self-information)越大,信息量就越大;重复的 Message 传递的信息量更少。他引入了衡量信息量的量 —— Shannon Information Content;一件发生概率为
的事件的香农信息量由下面的式子给出:
事件的信息由 SIC(香农信息熵)衡量,那么 随机变量的概率分布 的信息 由什么衡量?
假定
即离散型随机变量概率分布负对数的期望。信息熵越大,意味着随机变量的概率分布的不确定性越强(在一维离散型随机变量的概率分布中的体现就是,随机变量的每个可能取值的概率接近),说明它的信息量越大。
通俗地说,信息熵描述了有多少信息是无法确定的。信息接收了多少,熵就降低了多少。
或者说,熵是要消解事件不确定性的平均代价。
数学小提示:
你会在很多场合用到,可以通过换元法证明。简记为
0 log 0 = 0;
2.0.2 Joint Entropy & Conditional Entropy
说完了一维的情况,我们再讨论二维,或者更高维的离散型随机变量的信息熵。
高维离散型随机变量的概率分布是联合概率分布,以二维随机变量为例,联合熵定义为:
那么条件概率分布呢?这是我们已知条件(降低了信息熵)的基础上,求一件事物的信息熵。它的定义如下:
若
式子的含义是,在所有给定
如果是给定
但是,最好理解的方法还是 “熵的含义”:熵是对事件的不确定性。我们已知了
所以条件熵第二种算法,也是最简单、最通俗易懂的计算方法,就是
这就是信息熵的链式法则:
类比条件概率的链式法则:
说明熵的对数运算让乘除变为了加减。
以下是条件熵的特性:
2.0.3 Cross Entropy & Relative Entropy (KL Divergence)
那么,再考虑一种情况。我们之前都是正确掌握了随机变量的概率分布,并用这些信息构建了概率分布的信息熵的定义。
如果对于一个离散型随机变量,我们并不知道它的具体分布、只是模拟了近似的概率分布。这样的信息和真正的概率分布有差距,那这个概率分布的不确定性又该如何描述?
人们定义了 “交叉熵” 的概念,用来描述:在实际概率分布为
准确的定义是,对于同一个事件集上的两种概率分布
、 间的交叉熵,描述的是:如果编码方案采用针对 的优化,而非真实分布 的优化,那么平均需要从事件集中取出多少 bit 才能发现真实分布的情况。
这就相当于我们不知道
现在假设我们后来知道了
显然
;
数学上,可以用优化理论证明,
交叉熵和相对熵在机器学习领域(例如损失函数)使用颇多。它可以描述 当前估计的数据分布 相较于 真实数据分布 的偏差情况。
2.0.4 Mutual Information
如果两个随机变量不是相互独立的,那么它们必定在概率和信息熵上相关联。
就是说,一旦两个随机变量不相互独立,那么得到一个随机变量的信息,就会影响另一个随机变量的信息熵(就是从熵的角度理解两个非独立随机变量的条件概率)。
如何描述这两个随机变量的 “信息关联性” 呢?
人们定义了 “互信息” 的概念:一个随机变量所携带另一个随机变量信息的信息量。这个携带的信息量越大,那么这两个随机变量的相关性越强。
这个定义的含义是,假设分布
除了直接计算
两个信息熵相交的部分。
2.3 Choose the Parameter
现在我们如何确定模型参数
如果我们随机地选取一个
定义损失函数(loss function)来衡量
又称目标函数(objective function)、cost function;
负的损失函数又称为奖励函数(reward function)、利润函数(profit function)等等;
确定让损失函数最小的
进一步形式化这个问题:
给定一个数据集
其中
整个数据集的损失值定义为每个样本的损失值的均值,称为 Data Loss:
实际上你把模型输出的看作
这就转换成了优化问题,我们需要最小化目标函数(Data Loss):
首先我们现在研究 “选择什么样的损失函数对特定问题更合适” 这个问题。
2.3.1 How to Choose Loss Function
Multiclass SVM Loss
这个损失函数的思想是,正确的类型的得分,会远远高出不正确类型的得分。即不关心具体得分,只关心能否给出准确的 label。
注:我们将使用 Multi-class SVM Loss 作为损失函数的线性分类器称为 “SVM classifier”;
对于一个图像样本
Multi-class SVM Loss 给出:一个算法对 “ground truth 的得分大小和其他错误类比的得分大小关系” 与损失值的关系。绘图如下:
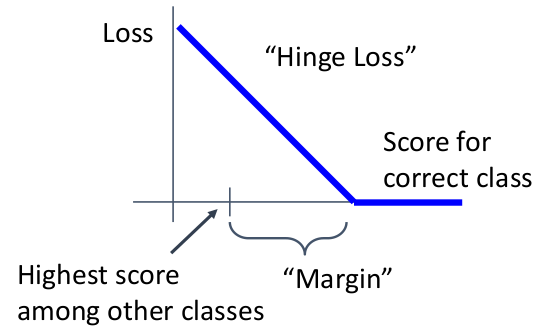
解读:当一个算法对 ground truth 判断的得分高出其他错误得分的差值越小(小于 margin 时),损失值会线性增大。
这种含有线性区域和零区域(水平区域)图像的损失函数,被称为 “Hinge Loss”(看起来像 door hinge);
我们记
因此这个损失函数的数学表达式可以写成:
解读:所有对于任意样本
,评分系统 在 上的损失 由所有不正确类型的得分( )和 ground truth 得分( )决定。 意味着只有正确类别比其他每个类别得分都要高出
才能实现无损失。 注意到:在一开始没有进行训练时,一个样本的损失值大约为
,其中 为分类数。因为 ; 为什么需要知道这个?因为我们需要一些 debugging 的手段(大概知道自己的模型有没有写错)。
显然,
拓展:
应该设置成什么值,是否需要 cross validation?这里先给出答案,你可以先看 “正则化” 一节后再来理解: 事实证明,在任何情况下都可以放心地将这个超参数设置为
。超参数 和正则化参数 似乎是两个不同的超参数,但实际上它们控制着相同的权衡:目标中 Data Loss 和正则化损失之间的权衡。理解这一点的关键在于,权重 的大小对分数(以及它们之间的差异)有直接影响:当我们缩小 W 内的所有值时,分数差异会变小,而当我们扩大权重时分数差异就会增大。因此确切值(例如 或 ) 在某种意义上是没有意义的,因为权重可以任意缩小或拉伸差异。因此,唯一真正需要权衡的是正则化参数 )。
Tips 1:如果把上面损失函数的求和换成求平均,这个分类器会不会有明显变化?答案是不会,因为将所有样本损失值同时乘以
Tips 2:如果将损失函数换成
Tips 3:假设我们找到一个
补充:Regularization(正则化)
在上面的 Tips 3 中,我们知道多个不同的模型参数
可以将正则化理解为,向目标函数(Data Loss)添加一部分,这部分不取决于训练数据,主要用来区分原来相同损失值的参数,也就是说,防止模型过拟合,阻止模型在训练数据集上 “做的太好”。例如新的 Data Loss:
这里
感性理解:让模型在训练时做些其他事,防止仅仅为了获得更低的损失而拟合。
对于线性模型(linear models),
L2 Regularization:
L1 Regularization:
Elastic Net(L1 + L2):
之后我们在神经网络模型中还会遇到例如 Dropout、Batch Normalization、Cutout 等等正则项的形式。
总结一下,目的具体如下:
表达在损失值标准以外的对模型参数的 preferences;
举个例子,假设一个线性分类器的表达式为
这时
一定程度避免 over-fitting 的问题;
注意过拟合问题:Overconfidence in regions with no training data could give poor generalization;
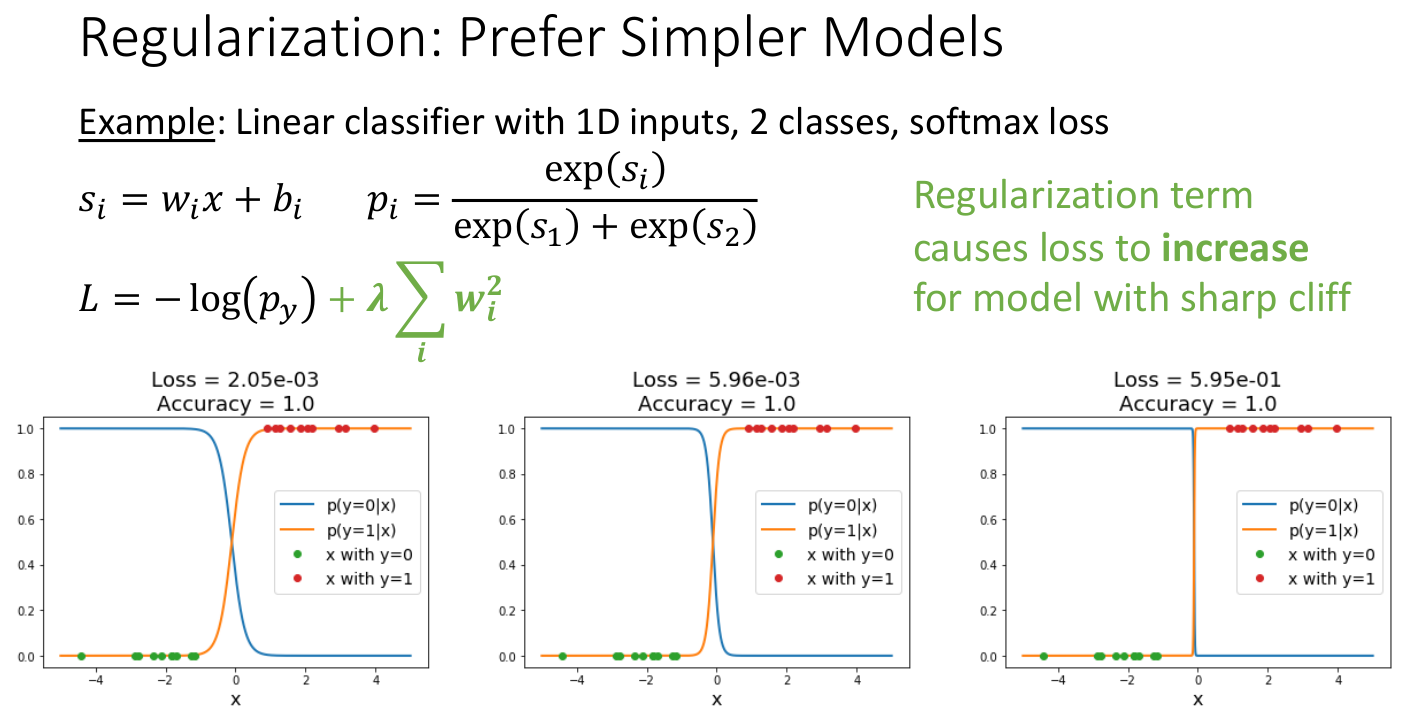
在某些情况下能改进现有的优化(改变现有模型在某些数据集上的“曲率”);
Cross-Entropy Loss (Multinomial Logistic Regression)
上面的 Multi-class SVM Loss 对应的损失函数只是简单地说明 “正确的类型有更高的得分”,并没有对模型具体得分的含义进行解读。如果我们希望让模型计算出的得分代表 “当前类别是正确的概率”,诸如此类的 preferences,则可以通过更换损失函数来实现。
这里介绍另一个经典的损失函数:交叉熵损失函数,使用它来做分类的方法又称为 “多项式逻辑回归”。
多项式逻辑回归是一种分类方法,它将逻辑回归概括为多类问题,即具有两种以上可能离散结果的问题。
也就是说,它是一种模型,用于预测给定一组自变量(可能是实值、二元值、分类值等)的分类分布因变量的不同可能结果的概率。
多项式逻辑回归还有很多其他名称,包括多项式 LR、多类 LR、softmax 回归、多项式 logit(mlogit)、最大熵(MaxEnt)分类器和条件最大熵模型。
多项式逻辑回归适用于因变量为 nominal 的(等价于分类变量 categorical,即两两间不能以任何有意义的方式排序的类别中的任何一类,通俗来说是不可比)。
我们将使用 Cross-Entropy Loss 的线性分类器称为 “Softmax Classifier”;
对任意一个样本-标签对
softmax 函数:
(之所以称之为 “softmax”,是指 “max” 函数的可导的近似函数,a soft differentiable approximation to hard max function);
可以让向量的各项介于 0~1 间,并且总和为 1(不至于像 max 函数一样大部分是 0,这使得网络中的一些计算难以进行);
可以借助指数函数特性(
),让两个不同的数值 大的更大、小的更小(凸显不同数据的差异); 其导数有很好的性质,方便计算交叉熵损失函数;
它在 “需要计算 max 特征”、“需要可导”的这些场景下比较有用。
注意到这是 softmax 函数。我们考虑模型对
我们回想一下,在概率学中,想要衡量 “在实际概率分布为
注意到
交叉熵损失值最小为 0(一般不会达到),最大为
; 注意到有意思的点:和 Multi-class SVM Loss 不一样,只有模型输出是 one-hot encoding(无比确定是某一类),并且恰与 ground truth 一致,损失值才会为 0。而前者只要求正确的类型得分远高于错误的类型得分。
debugging trick:在一开始没训练时(
随机),一个样本的损失值大约为 (每个类型的概率相当);
补充:Softmax 函数的数值稳定性
在实际场景中,计算 softmax 函数的
你可以在 Python 中试试:
xxxxxxxxxxf = np.array([123, 456, 789])p = np.exp(f) / np.sum(np.exp(f)) # Oops! inf appears!很不幸地,
由于出现了 溢出没法继续正常参与运算了!
我们一般需要通过一些标准化的措施(例如数学变换)来缓解这样的问题,就 softmax 这个函数而言,一般的做法是同乘一个任意非零常数
并且取
在 PyTorch 里面,有专门帮助 softmax 这样可能出现数值稳定性问题的运算函数避免问题发生,例如 torch.logsumexp(),里面就实施了一系列保证数值稳定性的措施,你可以放心地调用它来计算
2.3.2 How to Do Optimizations
现在我们为线性分类器模型形式化了优化问题、建立了损失函数的数学模型。现在我们需要了解如何解决这个优化问题,也就是说,如何利用损失函数来优化获得更好的
回想之前优化问题的定义:
Random Search
随机生成参数矩阵
注意到随机生成实际上不能解决我们的问题,我们需要更加智能的算法。
Follow the Slop (Gradient Descent)
另一种比较常用的方法是梯度下降,我们一般可以通过这个方法至少获得一个局部最优解。
回忆一下多元微积分中的方向导数、梯度的定义。
方向导数:函数定义域的内点对某一方向求导得到的导数。以二维函数为例:
方向导数代表了在某点
注意到:
梯度向量的方向,正是函数值在该点增大最快的方向;
梯度向量的长度,正是函数方向导数在特定点上的最大值(绝对值),
我们梯度下降算法就是给定步长,从某点选择梯度下降最快的方向迭代前进,直至梯度消失。
不过我们给定的样本数据是离散的,如何在离散的数据集上计算?
一种方式是 Numeric Gradient(数值梯度)。我们建立一个与
问题:
这种方法的问题是时间复杂度
而且限于计算机数据表示方法,
而且这在有些时候会出现数值不稳定性(例如梯度即将消失时,分子分母都是很小的小数)。
另一种方法是 Analytic Gradient(解析梯度)。这里因为我们研究的是线性分类器,因此从解析式的角度考虑准确的情况是可能的!以后我们讨论任意复杂的模型时,解析法可能就不再好用了。目前我们只想得到
如果解析解可行的话,我们通常同时使用解析梯度和数值梯度,并使用后者验证前者(gradient check)。
我们可以在 PyTorch 框架中看到 pytorch.autograd.gradcheck(func, inputs, eps, ...)(还有 gradgradcheck,检查二阶导)这样的方法来做梯度验证。
不需要验证三阶导,因为 PyTorch 的实现方式,只需要验证
gradcheck和gradgradcheck,任意阶导的正确性就能保证了。
现在考虑 Gradient Descent 算法的整体框架:
xxxxxxxxxxw = initialize_weights()for t in range(num_steps): dw = compute_gradient(loss_fn, data, w) w -= learning_rate * dw算法本身比较简单,不过有一些超参数:
权重初始化参数;
迭代步数;
学习率;
这些超参数和 KNN 的超参数不一样,后者在实践中调整的必要性和重要性不大,但是梯度下降的超参数会极大地影响模型的 performance 和效果(有时能达到 30% 左右的差距)。
其中,迭代步数在大多数深度学习应用中越大越好,主要的限制在于你的计算资源的预算以及希望的时间开销。
学习率决定了一次迭代前进的步长(模型一次学习多少),有一种方法是让它取决于当前函数的梯度大小。梯度较大时学习率越大,梯度较小时学习率小(接近最优解时不再 “大步流星”,而是“小碎步”接近)。
Further: Stochastic Gradient Descent (SGD)
上面的梯度下降算法实际上有个问题,在执行 compute_gradient 时,如果是解析梯度,那么就需要计算:
如果数据集相当大(上亿),那么计算仅仅一轮迭代就要花费相当长的时间。于是人们想出一个好办法:仅仅从样本中抽出一部分(被称为 batch)来计算梯度,而这部分的大小被称为 batch size,伪代码如下:
xxxxxxxxxxw = initialize_weights()for t in range(num_steps): mini_batch = sample_data(data, batch_size) dw = compute_gradient(loss_fn, mini_batch, w) w -= learning_rate * dw使用数学表达:
原来的方法被称为 “full batch”。这时我们再次引入了两个超参数:batch size 和 采样方法(sample_data)。其中 batch size 人们在实践中一般使用 32 或 64 或 128 这样的数。
注:Batch Size 本身受限于 GPU memory 大小,过小的 batch size 无法起到很好的采样效果。不过也不是越大越好。有相关研究表明,在某些情景下过大的 batch size 会导致收敛到最优值的速度减慢,甚至无法到达最优值。
采样方法可以是随机选取,或者每轮 shuffle 再取,在图像分类这一情景下区别不大。但是在 structured prediction problem(结构化预测问题)、triplet matching problem、ranking problem 这些情景下,采样方法就比较重要了。
为什么这种方法被称为 “Stochastic”(随机的)?
我们可以将损失计算视作对全样本空间数据分布(
但是 vanilla SGD 算法在某些场景/问题下效果不佳。
高曲率/小峡谷问题。我们考虑一个数据分布的场景:如果 loss function 在某个方向上变动剧烈,而另一个方向上变动缓慢(在二维空间中表现为扁椭圆形的等高线分布,我们称损失函数的 contour 图为 “损失面”),这时我们无论选择 learning rate 较大还是较小,收敛速度都不好。较小的 learning rate 本身收敛速度有限,而较大的 learning rate 会导致震荡(我们称这种现象为 “过冲”,overshooting):
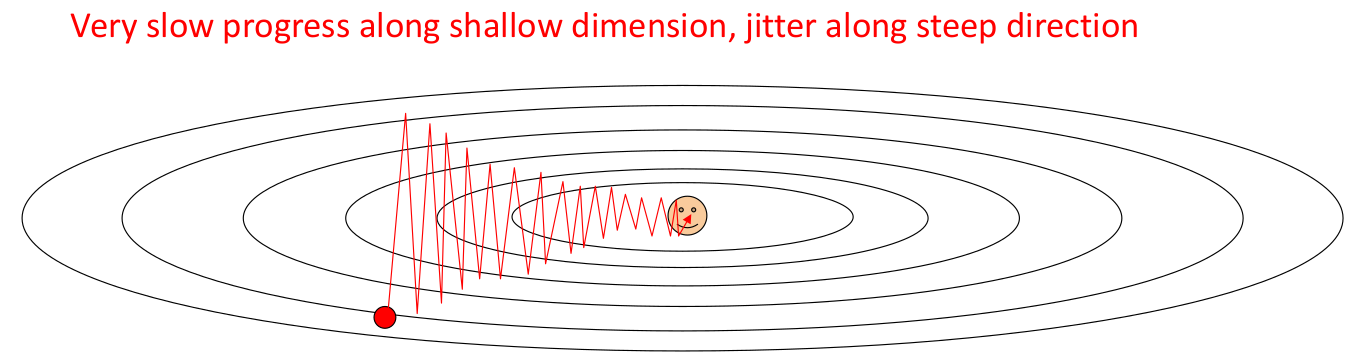
我们在数值分析中,将这种情况称为 high condition number。Condition number 描述的是前向误差和后向误差的比例关系。
在一个矩阵中也有 condition number,它描述的是它接近奇异矩阵的程度。
我们可以计算某点处的 Hessian Matrix(二阶偏导矩阵)的特征值比例情况来评估 condition number;
再考虑一个数据分布场景。以二维点为例,如果损失函数呈现出马鞍形(即存在局部最优不等于全局最优的情况),通常情况下没法找到最优解。因为 SGD 会在接近局部鞍点时错误地收敛(鞍点处梯度为 0),影响整体的训练效果。
取样噪声。有些数据集的局部样本存在很大噪声,会导致梯度下降的过程呈现四处游走的情况,不能很好地符合实际梯度下降方向。
为了缓解以上问题,我们在训练神经网络时通常使用 SGD + momentum(有动量的、有惯性的)的策略。这里我们借鉴了物理学的思想,每次步进不是直接使用梯度,而是让梯度作为 “加速度”,来改变 “速度”(
对应伪代码:
xxxxxxxxxxv = 0for t in range(num_steps): dw = compute_gradient(w) v = rho * v + dw w -= learning_rate * v我们可以感性地了解为什么有动量的 SGD 可以缓解上述问题:对于 pool conditioning 的损失值分布,曲线会更加平滑、收敛也会更快(想象自己放下了一个遵循物理定律的小球);对于含有鞍点的损失值分布,模型能够有概率跨过鞍点的限制;对于取样噪声,则会因为速度的引入而被极大地克服。
还有另外一种处理方式,也就是更新速度时使用 look ahead 的方法(事先更新下一轮的损失值,让学习率参与其中):
这种方法被称为 Nesterov Momentum,它能够但是这样的计算方法没法很好地利用一些优化的函数。因此通常情况下我们会做一些数学变换,设
对应下面的伪代码:
xxxxxxxxxxv = 0for t in range(num_steps): dw = compute_gradient(w) old_v = v v = rho * v - learning_rate * dw w -= rho * old_v - (1 + rho) * v对比一下两种动量实现的优劣势:
Nesterov Momentum 优势:
更快的收敛速度
Nesterov Momentum 在计算梯度时,先基于当前动量方向进行一次“预更新”(临时参数位置),再在此位置计算梯度。这使得梯度方向更贴近实际更新后的参数位置,减少了震荡,尤其在凸优化问题中理论收敛速率更优(从
对于非凸问题(如神经网络),实践中也常观察到更快的收敛,尤其是在高曲率或复杂地形(如“峡谷”形损失面)中。
更稳定的更新方向
通过预更新后的位置计算梯度,能更早感知参数更新方向的变化,减少过冲(Overshooting)风险,尤其在动量系数较大时表现更稳健。
更好的逃离局部最优能力
提前的梯度计算可能帮助跳出局部极小或鞍点,因为动量方向结合了未来位置的梯度信息。
Nesterov Momentum 劣势:
实现复杂度略高
需额外计算临时参数的梯度,但在现代深度学习框架(如 PyTorch、TensorFlow)中已封装,实际使用无显著差异。
超参数敏感性
虽然动量系数通常与普通 Momentum一致(如 0.9),但最佳学习率可能需要微调,尤其在噪声较大的数据分布下。
理论保证局限
对非凸问题的理论分析较困难,实际效果依赖任务和数据特性。
总而言之,我们在多数场景下应该优先使用 SGD + Nesterov Momentum 的方案。
Adaptive Learning Rate Algorithms: AdaGrad, RMSProp, Adam
上面我们讨论的 SGD + 各种 Momentum 的方法都是固定学习率的,我们来考虑如何将学习率也加入优化的讨论范围中。
之前我们提到了超参数 “学习率” 的一种取法,就是随着当前梯度大小来决定学习率大小。这种思想就是 “自适应学习率优化算法”(Adaptive Learning Rate Algorithm),主要针对不同参数的历史梯度信息来调整学习率。
现在我们在 SGD 的基础上考虑一种新的自适应学习率的优化策略:让 learning rate 除以历史梯度平方累积的开方,作为当前轮的实际学习率。这种方法也可以缓解 overshooting 的现象,并且在一定程度应对 pool condition 的损失面。
这种策略被称为 AdaGrad,其计算方法如下(在普通 SGD 前提下引入自适应学习率):
xxxxxxxxxxgrad_squared = 0for t in range(num_steps): dw = compute_gradient(w) grad_squared += dw * dw # 累积历史梯度的平方 w -= learning_rate * dw / (grad_squared.sqrt() + 1e-7)它的思路是,在梯度变化剧烈的方向上减缓(damped)学习,在梯度变化剧烈的方向上加速(accelerated)学习。
至于为什么要累积历史梯度的平方,一是想消除符号影响,避免累积时正负抵消(就像方差一样);二是想放大梯度的影响,使算法更关注那些波动较大的参数。
至于为什么除以累积的开方,一是想保证量纲一致性,二是稳定学习率更新幅度,防止避免学习率过早衰减到零。
至于为什么要加上 1e-7,是为了防止除零问题。
但这么做还是有问题,因为随着训练时间延长,grad_squared 会不可避免地非常大(单调增长),这会导致在很多情况下,到达最优解之前学习率减为 0。
于是人们在 AdaGrad 的基础上提出 RMSProp 来缓解这个问题。RMSProp 的思想是仍然计算梯度平方的历史累积值,但是让历史值自身逐渐衰减,防止学习率快速衰减(就是普通 SGD + 历史衰减的 AdaGrad):
xxxxxxxxxxgrad_squared = 0for t in range(num_steps): dw = compute_gradient(w) # 历史数据乘以 decay_rate,当前梯度平方数据乘以 1-decay_rate # 引入指数衰减平均,侧重近期梯度 grad_squared = decay_rate * grad_squared + (1 - decay_rate) * dw * dw w -= learning_rate * dw / (grad_squared.sqrt() + 1e-7)这可以理解成一个 “leaky AdaGrad”,每次丢失一定比例的历史梯度累积数据,保证学习效果。实践证明,在一般的损失面上,RMSProp 比 SGD + Momentum 的收敛速率慢点,但是很少有 overshooting 的情况。
那么,为什么不强强联合,让 RMSProp 和 SGD + Momentum 一起使用呢?是的。人们提出另一种优化学习率的方法就是将 RMSProp 的思想和 Momentum 的思想结合,这被称为 Adam 算法。其大致思想如下:
xxxxxxxxxxmoment1 = 0moment2 = 0for t in range(num_steps): dw = compute_gradient(w) # velocity simulation moment1 = beta1 * moment1 + (1 - beta1) * dw # leaky grad_squared moment2 = beta2 * moment2 + (1 - beta2) * dw * dw w -= learning_rate * moment1 / (moment2.sqrt() + 1e-7)这样就可以了吗?不对,考虑一种情况,
xxxxxxxxxxmoment1 = 0moment2 = 0for t in range(num_steps): dw = compute_gradient(w) moment1 = beta1 * moment1 + (1 - beta1) * dw moment2 = beta2 * moment2 + (1 - beta2) * dw * dw moment1_unbias = moment1 / (1 - beta1 ** t) moment2_unbias = moment2 / (1 - beta2 ** t) w -= learning_rate * moment1_unbias / (moment2_unbias.sqrt() + 1e-7)引入了随时间负指数变化的偏移量 moment1_unbias 和 moment2_unbias 有助于克服原来算法在
好了!目前这个 Adam 算法,加上常用的超参数(
Optimizations With Regularization: Weight Decay & AdamW
这一节我们讨论优化的时候都是将
我们在选取损失函数时曾经提到,可以在损失函数中使用正则化项来对模型进行正则化:
人们常将正则项写成
,就是因为常常取 L2 Regularization,为了在运算梯度时不需要前缀一个 2 这个常量。
这时,正则项就成为 “削减” 权重的项,因此这种传统的正则化手段又称为 权重衰减(Weight Decay)。
我们注意到,这种正则化方法有个缺点,就是权重衰减项是和学习率耦合的!如果我们采用自适应学习率优化算法,那么正则化的效果势必会受到学习率 / 历史梯度数据(如果用的是 Adam 这样的自适应学习率算法)的变化的影响,正则化效果不稳定。
因此,为了防止 Adam 这样的自适应学习率优化算法无法稳定地正则化,人们基于 Adam 设计出了新的方法:AdamW。它的思想是将权重衰减项(正则化项)与梯度更新(学习率)解耦,也就是,将权重衰减项不再放在损失函数中实现(损失函数中不包含正则化项,只含原始 Data Loss),而是在更新权重的优化算法中直接引入权重衰减项:

人们发现:
Adam:适用于不强调精细控制权重衰减的场景,或模型较小的情况。
AdamW:在需要严格正则化的大型模型(如 Transformer、ResNet)中表现更好,尤其是在结合预训练模型时效果显著。
Further: Second-Order Optimizations
上面我们讨论过的优化算法 SGD 及其变式,其实都是一阶优化,也就是按照损失面的一阶(偏)导来决定更新的方向,这相当于对原来的损失面采用了线性近似的方法来训练和迭代权重。
不过实际上我们也可以进行二阶优化,相当于用二次曲线/二次高维曲面和 Hessian Matrix 对损失面做二次近似,这在某些情况下可以提高收敛速率并提高鲁棒性。我们用在
其中
这种方法被称为 L-BFGS 二阶优化方法。
但这种方法并不常用,主要是因为
Summary
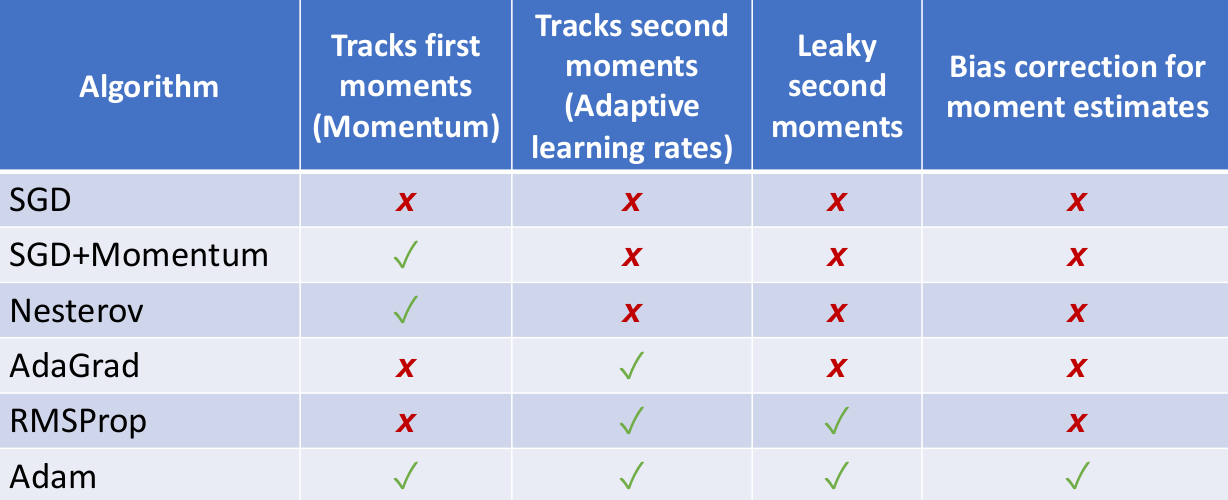
总而言之,Adam 和 AdamW 是一个在各个场景下比较通用的优化算法;SGD + Momentum 有时可以超过 Adam,但是需要更多调优(tuning)的工作。
如果你面临的问题是低维的,或者并不服从概率学规律(不是 stochastic 的),你可以尝试使用 L-BFGS。
Lecture 3. Neural Networks
在 2.2 中,我们已经认识到了线性分类器的局限性:
使用 template vectors 进行相似度比较,有 “过拟合” 的嫌疑;
得分会随着图片整体信息(例如调整亮度)而影响,bug or feature?
不能很好地模式识别。例如汽车的不同颜色、马头的不同朝向,全会纠缠在 template vector 中;
一定没法对某些数据类型划分。例如无法模拟 XOR、“分布在多组相反对角线上的” / “以半径为分布特征” 的数据 等等。
人们曾经想对线性分类器进行改进,试图克服上面的局限性。一种解决方法是 Feature Transforms,它主要想解决线性分类器对特定数据类型无法划分的问题。
它的思想是,通过对样本数据(例如以半径为分布特征的数据)进行某些数学上巧妙的变换(例如直角坐标到极坐标),从 original space 变换到 feature space,最终让线性分类器有办法分类它,有种专家系统的意味在里面。这种技巧被用在很多机器视觉算法中(例如 color diagram、Histogram of Oriented Gradients (HoG))。
这种方法的问题也很明显,就是你需要非常了解样本数据的特征,并且还需要非常了解各种变换的数学手段。
在图像领域,人们还讨论了 bag of words 方法,试图通过构建 “code book of visual word” 来不依靠专家指定转换方程。人们甚至可以将 color diagram、HoG、bag of words 结合起来作为一个图片对应的特征向量,以此利用线性分类器的效果会更加好。
这个过程就被称为 特征提取(feature extraction)。
这种特征提取 + trainable model(线性分类器)的方法也能组成一个分类器流水线(classifier pipeline),但是它仅仅能在 model 这一 final layer 中 tuning 自身(训练权重),而特征提取的 layer 则没法优化自身的参数。这也说明了这个模型有待改进。
因此,人们希望构建出一个 end-to-end pipeline,接受 raw pixels,输出类别的评分,并且实现系统内全部参数自调节(不仅是含有线性分类器的这个 layer),这就是神经网络最初的目标,它会同时学习特征提取和表示,以及像线性分类器一样的多个参数。
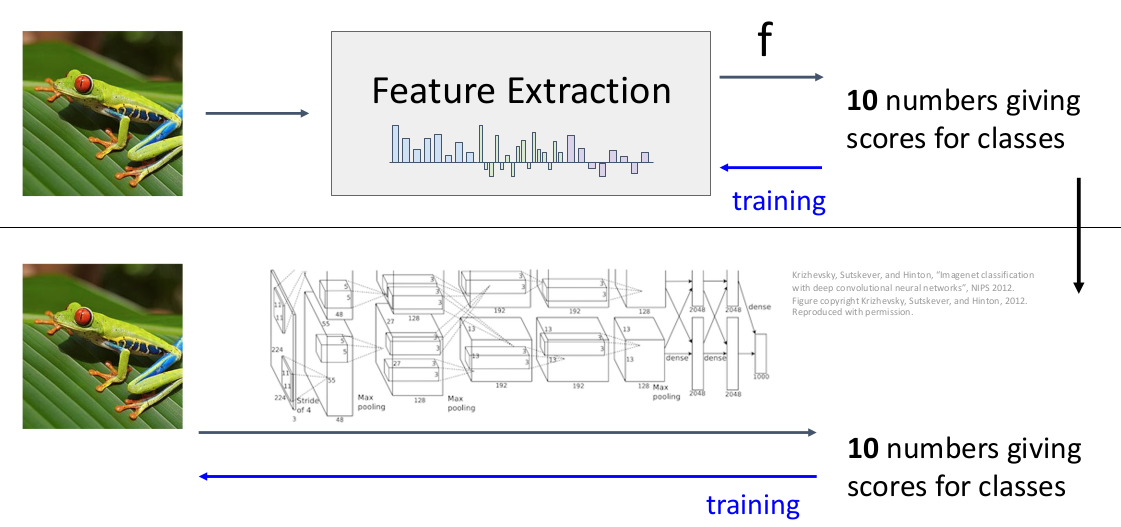
3.1 Definitions
现在对比之前的线性分类器
其中
问什么神经网络要这么设计(
函数、多次矩阵相乘)?我们等会来分析一下。
回到那个两层神经网络的例子,每层神经网络中的权重(
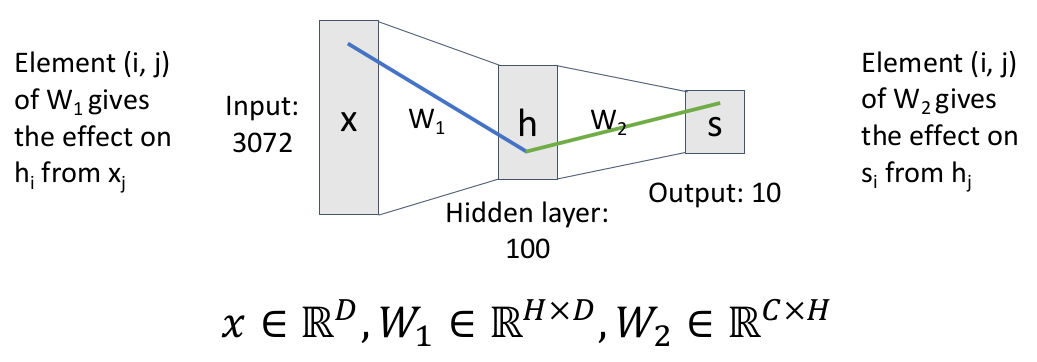
如果我们运算的方法就是上面的矩阵乘法(就是上面定义的方法),也就是说上一层的每个元素都能影响到下一层的每个元素,这时我们称这层网络为全连接网络(fully connected network),这种网络结构也被称为 “多层感知机”(Multi-Layer Perceptron,MLP)。
那么
但大多数情况下,这个划分不一定是 human interpretable 的,可能只是有一些特殊的 spatial structures。
这就是神经网络神奇的地方,你并不知道具体需要学习哪些特征,只是通过优化的方法让这个分类器学习那些能最大化分类准确性的特征。
神经网络就是利用这些 “distributed representations”,通过第二层矩阵乘法对这些 template vectors 再次进行线性组合,试图将这些同类不同模式的 template vectors 打分更高。
这些第一层网络学习特征的关键就是图像中的 “oriented edges”(边缘朝向)和 “opposing colors”(高对比度的颜色)。类比人类的视觉识别,在暴露在不同图像曲线的情况下大脑中的不同部分的神经元会被差异化地激活,并且这些激活的情况和图像的边缘朝向有强烈关系。
第二层网络则是学习组合这些特征来解释图片中出现不同结构的类型,这样说神经网络似乎直觉上就更有合理性一些。
这些中间学习到的抽象的、不是 human interpretable 的特征信息的层又称为 “隐藏层”(hidden layers)。
这期间可能学习到一些冗余的信息,我们后续可以通过正则化,或者手动设计网络结构/filters、微调/量化 来缓解这个问题。
在这个基础上,人们就不由得会尝试泛化到更多层神经网络,这就是深度神经网络(Deep Neural Networks):
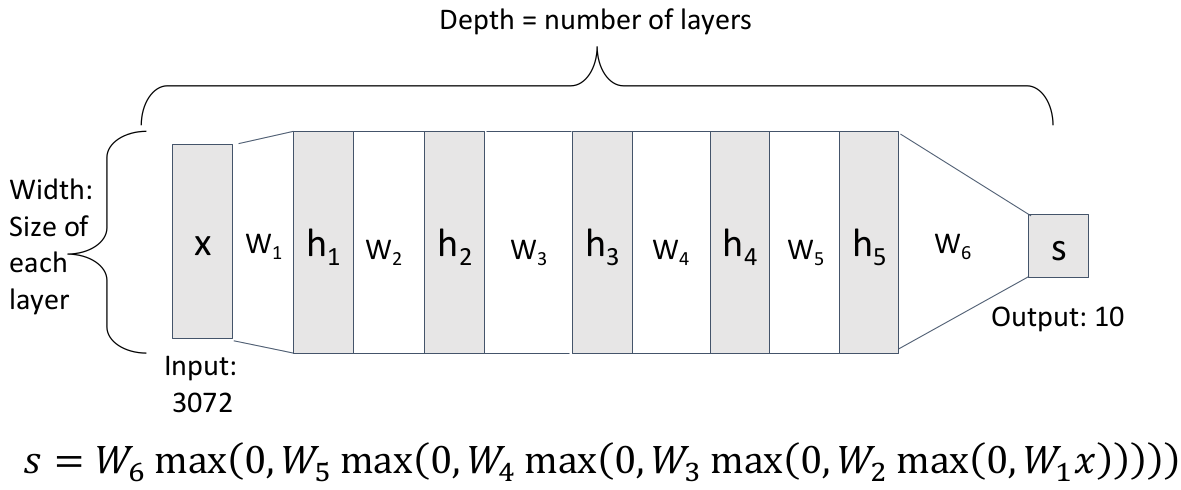
深度神经网络的深度就是包含可训练的参数矩阵
3.2 Activation Functions
现在我们回到之前的问题上,全连接神经网络

我们从两个方面考虑为什么需要激活函数、为什么要这么设计神经网络。
一方面,如果没有激活函数,我们只是定义
旁注:有一类问题 “deep linear networks” 就是学术界在研究理论计算优化时讨论的问题,虽然它的特征描述能力和一般线性分类器相同,但是数学优化方法上更为困难。因此它在理论研究领域还是有用处的。
另一方面,思考激活函数本身的特征。人们选取这些激活函数实际上是对于人类神经元运作机制的模仿(这也是被称为 “神经网络” 的原因),考虑生物体中的神经元作为思维和计算的基本单元:
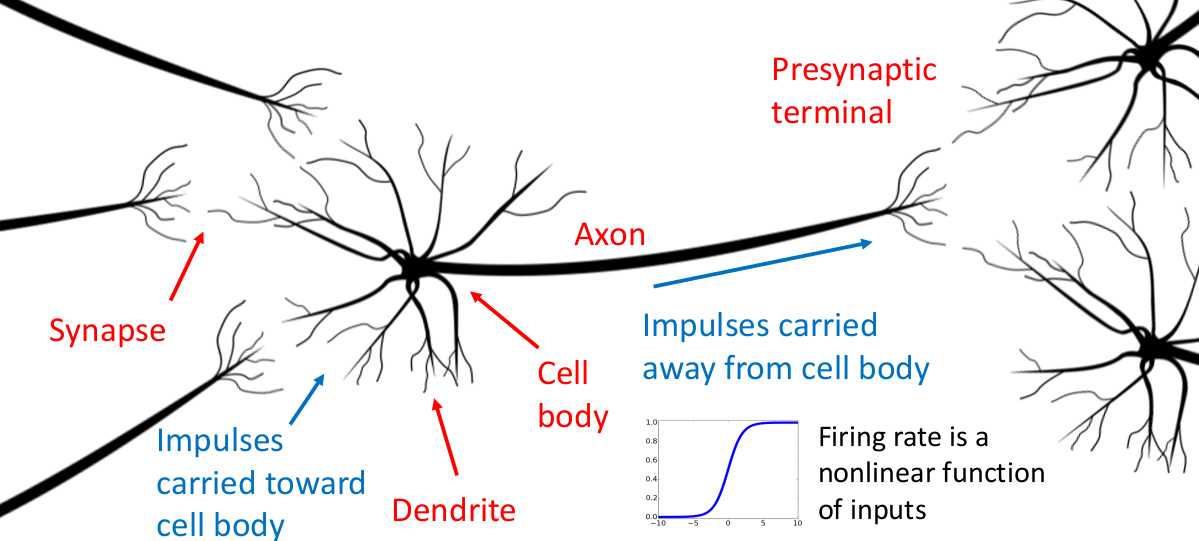
树突(Dendrite)为神经元的输入通道,其功能是将自其他神经元所接收的动作电位(电信号)传送至细胞体内;在细胞体内经过处理和电位变化后,由包裹着髓鞘(Myelin)的轴突(Axon)传递给输出单位 突触(Synapse,神经元与肌细胞、腺体之间通信的特异性接头),中枢神经系统中的神经元以突触的形式互联,形成神经元网络。这对于感觉和思维的形成极为重要。
人们注意到,一个神经元输入信号和输出信号的关系取决于这个神经元具体接收的信号的情况,每种信号有不同的激活阈值、激活权重,这些权重和阈值与神经元历史 “学习” 到的信息、细胞本身所处的电化学环境等等因素有关。
于是我们将神经元抽象成数学模型:
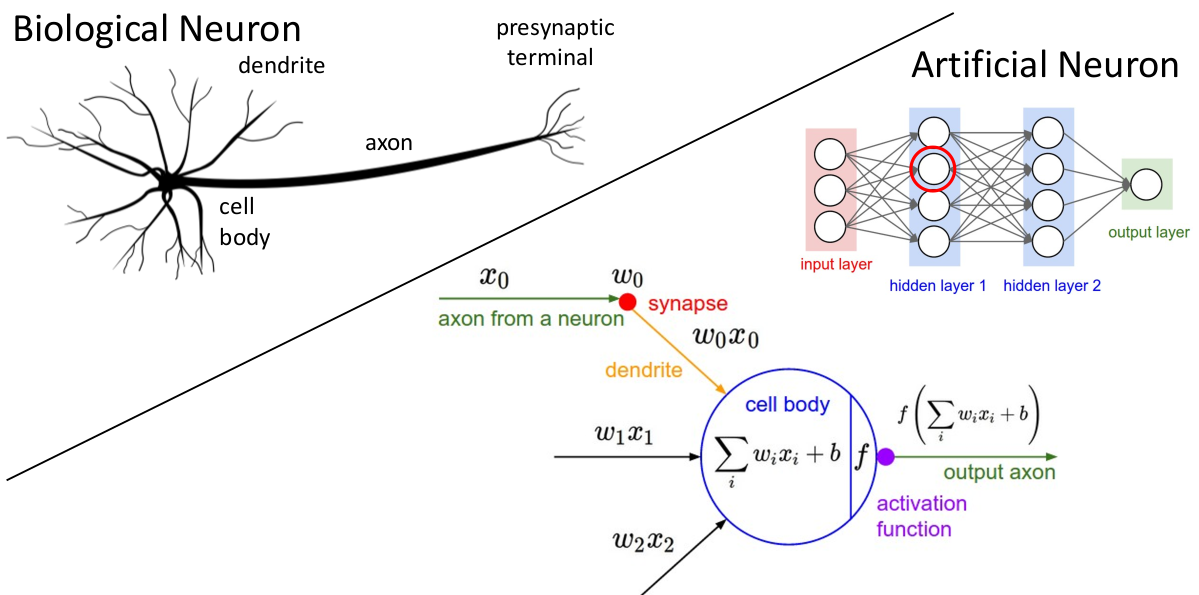
其他不同神经元的轴突传来的信号有不同激活权重(对应着之前我们每层网络中的参数矩阵),细胞体相当于对输入信号做汇总运算,并且只有当汇总信号突破激活神经元轴突的阈值(对应模型中每层的 bias 偏置量)时,才会输出汇总后的信号,否则不会输出信号。这个 “判断” 过程并非线性。
因此人们模仿神经元的激活过程,根据不同情况下的计算需求,设计了上面几个激活函数,相当于实现了这个神经元的激活过程。
但人工模仿的神经元和生物神经元间还是有相当大的差异,例如不同的连接方式、不同的神经元类型、每种神经元处理信号的方式等等。
我们不能从理论上说明这样做的正确性以及有效性。那么为什么我们还是选择这种方式来构建网络作为分类器呢?
另一种视角的说法是 Space Warping(空间扭曲)。
回想我们在线性分类器中讨论过代数几何的视角,每个数据点都对应于高维空间中的某点,线性分类器的参数矩阵一行则代表高维欧式空间的一系列超平面的划分,沿这个超平面垂直方向前后移动则代表对应类型得分的增减。
线性分类器做的参数矩阵乘法,就相当于对整个数据空间以这些垂直方向为新坐标系进行的线性变换(变成 “feature space”)。
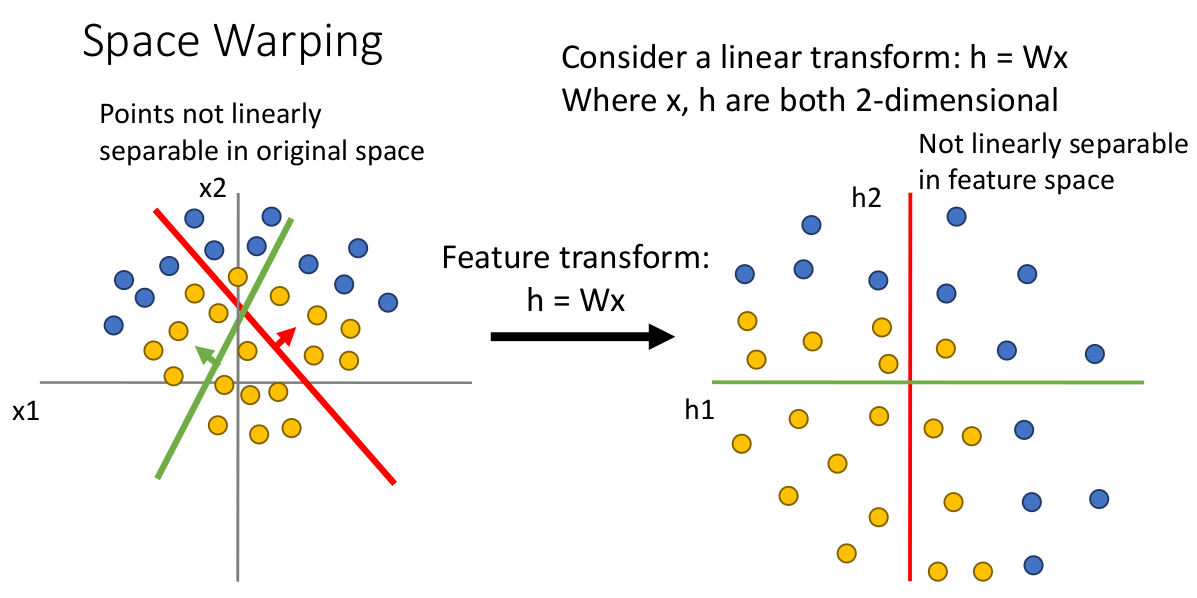
如上图,由于变换的线性性,原来非线性分布的数据点,在关于特征超平面的线性变换后仍然是非线性的,因此这种数据始终没法使用线性分类器很好地描述与分类(线性不可分的)。
这也解释了为什么之前说 deep linear networks 对增强模型描述特征的能力方面没有任何帮助。
但是如果我们将激活函数作用于数据点后,数据空间中负值象限(注意这里只是方便理解,实际在高维空间很难这么描述)的所有数据点全部 collapse 到坐标轴或者原点上:
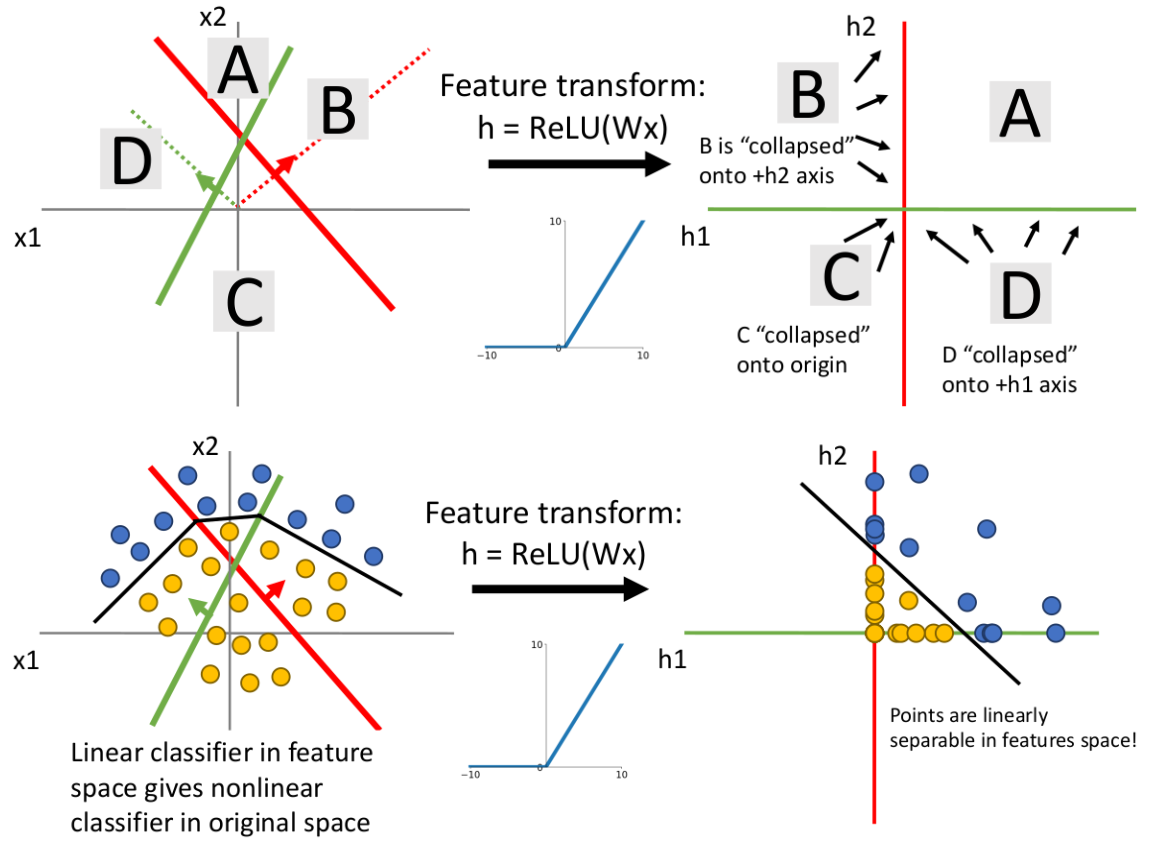
我们发现原来线性不可分的数据分布在 ReLU 的转换下变得线性可分(在 feature space 下线性可分。原来的 decision boundary 在 input space 中不再是线性的了),我们可以通过简单地再加一层线性分类器就能出色地完成分类任务!
这个例子有力地说明了神经网络及其非线性的激活函数,相较于线性分类器有更强大的特征描述和分类能力。这也是激活函数、神经网络更有意义的原因。
我们再继续从感性角度理解一下多层神经网络的意义。对于一组特定的二维数据,不同深度的神经网络能达到的分类效果:
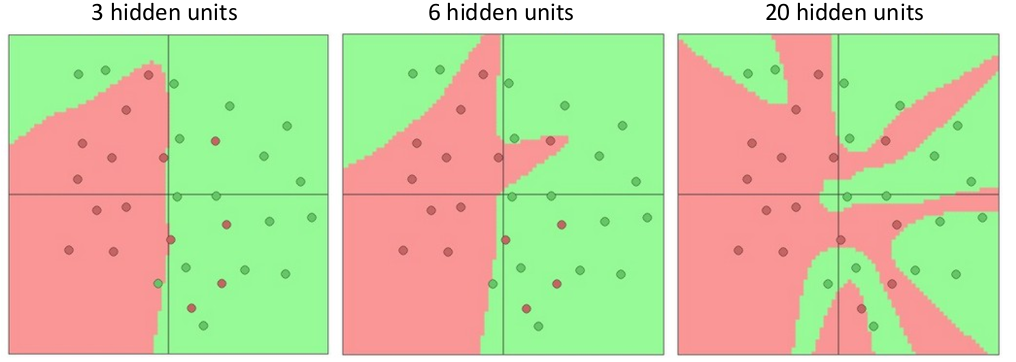
注意到更多的层数意味着 decision boundary 可以描述的特征越复杂。
这里敏锐的读者可能发现一个问题,层数越深(模型复杂度越大),网络描述细节的能力越强,那么深层神经网络在层数很大的时候会不会出现过拟合的现象?尤其是数据集中的噪声影响,所以和线性分类器一样,这涉及到了模型的正则化。
3.3 Regularization in Neural Networks
在神经网络中如何进行正则化?神经网络中的正则化在感性上来看是什么样的?
首先明确一点,在神经网络中,我们不应该对网络的大小(即宽度和深度的统称,理解为网络的架构)直接正则化,而是在网络中设置一些 tunable regularization parameters(可微调的正则化参数),然后直接对参数调整。
这时候我们可以复用之前定义的 L1、L2 regularization / elastic net 这样的正则函数。同样的,它们的作用是 smoothen decision boundary、降低模型冗余复杂度、防止过拟合、表达对 unseen data 的 preferences,并在某种程度上提升模型分类效果。如下图所示:
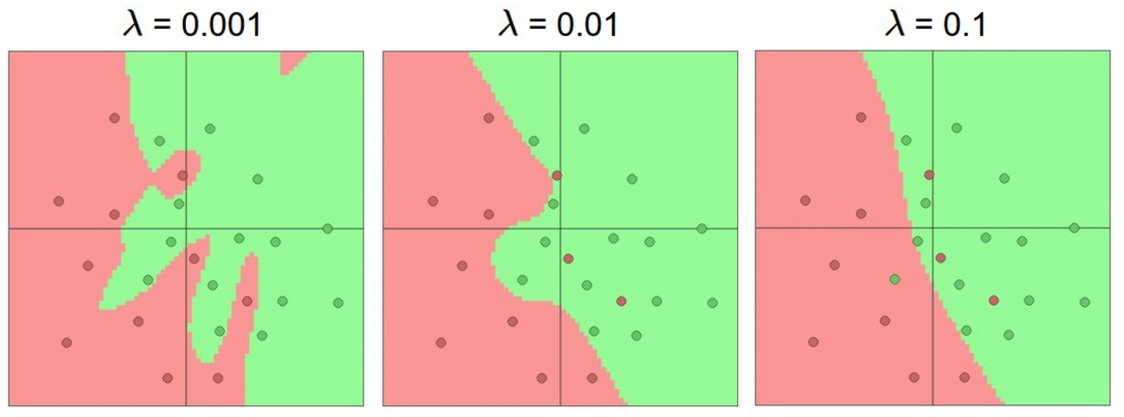
3.4 Revisit: Universal Approximation
在建立对神经网络的直觉后,我们发现神经网络能够描述比线性分类器更多、更复杂的分类情况。我们将这个特性规范化一下,称之为网络的拟合通用性。
数学上可以证明,含有一个隐藏层的神经网络可以以任意精度,拟合任何函数
这里实分析会定义 “任意精度”、说明函数的连续性、
的实子集等等,这里略过理论知识。
这里我们认为神经网络模型已经本质上超越了线性分类器模型,拟合任意线性不可分的数据情形。我们看一个最简单的例子,对于一个
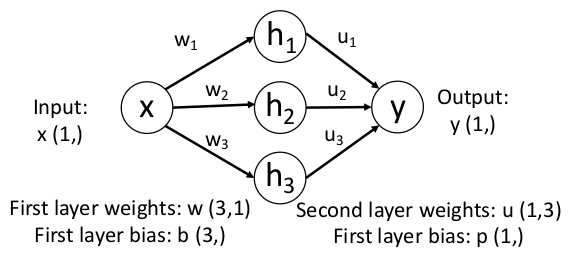
注意到它们是一系列非线性函数的线性组合,这样只要我们将非线性函数作为 “基底”,且 “基底” 足够多,总能拟合出目标函数。
再以 ReLU 激活函数为例,假设需要拟合一个 bump function,我们一定可以由四层神经网络完美拟合:
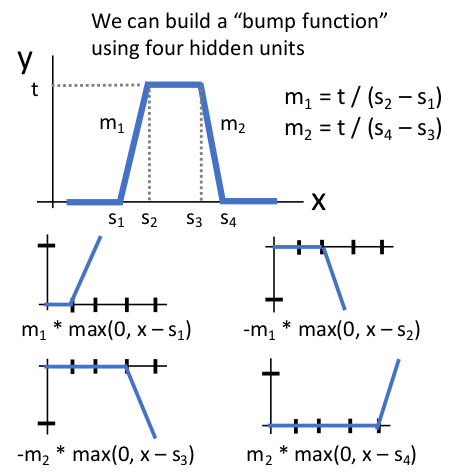
根据信号与系统的知识,我们知道由多个这样的 bump function 作为基本单元并线性组合,就能拟合出任意连续函数。也就是说,只要神经网络的隐藏层足够多,这样的基本单元就足够多,我们就能够更准确地拟合各种信号,这也从直觉上解释了神经网络多层的意义。
这里只是直觉上。实际理论上确实可以证明它的通用性,但需要严格证明,如何适用于其他非线性函数、如何适用于更高维的情况,事情就比较复杂了。感兴趣查看:Proof;
不过上面只是理论上神经网络可以拟合任意非线性情形,没有告诉我们如何设置这些权重、需要多少数据集以多少计算复杂度来得到这个结果。因此不能因为它具有这个性质就说神经网络是最好的数学模型(就像 KNN 有 Universal Approximation 性质一样)。
但实际训练这些神经网络时,它们在收敛时并不会像理论那样(比如组合出所谓的 bump function),而是某个解决方案,但实际效果也确实比线性网络更好。
另外值得一提的是,目前为止无论是线性模型、L1/L2 正则项、softmax 函数、SVM 模型,它们都是凸函数,意味着线性分类器问题总是在优化凸函数,它注定有局部最优等于全局最优,并且不依赖于初始条件,永远是收敛到解的。
但神经网络模型对应的优化模型通常不是凸函数,因此没有收敛性和最优解的保证。
3.5 Gradient Descent in Neural Networks & Optimizations
不像线性模型,想要在神经网络中计算梯度并学习是个比较难的事情。注意,如果你希望写出神经网络的梯度的解析形式并且计算,这个做法就是错误的。原因比较容易理解:
含有许多矩阵运算,运算极其繁琐;
如果希望更换损失函数,整个优化过程需要从头开始计算,不具备模块化的能力;
(not scalable)无法自动推导所有解析式的梯度。因此如果模型本身就很复杂,实际上获取解析梯度本身就是不可行的;
从计算机学家的角度来说,我们要做的不是怎么设计出推导通用的计算梯度的工具(事实上这对于数学家也很难),而是应该利用恰当的数据结构和算法来帮我们完成这些繁琐的任务。于是人们提出了 “计算图” 的概念。
3.5.1 Computational Graphs & Back-propagation
计算图是一个有向图,用于表示一个模型内部需要进行的运算,通过模块化、流水线化的形式充分利用机器计算资源(调度、并行)、减小计算成本。
神经网络可以使用计算图方法来动态计算网络的梯度值并进行学习,可以说这个数据结构使得 NN 优化成为可能。
源结点表示输入参数、汇结点表示计算结果,其余结点表示特定计算过程;
边表示数据传输信道(communication channel);
例如一个使用 Multi-class SVM Loss 作为损失函数的线性分类器的损失函数计算图如下:
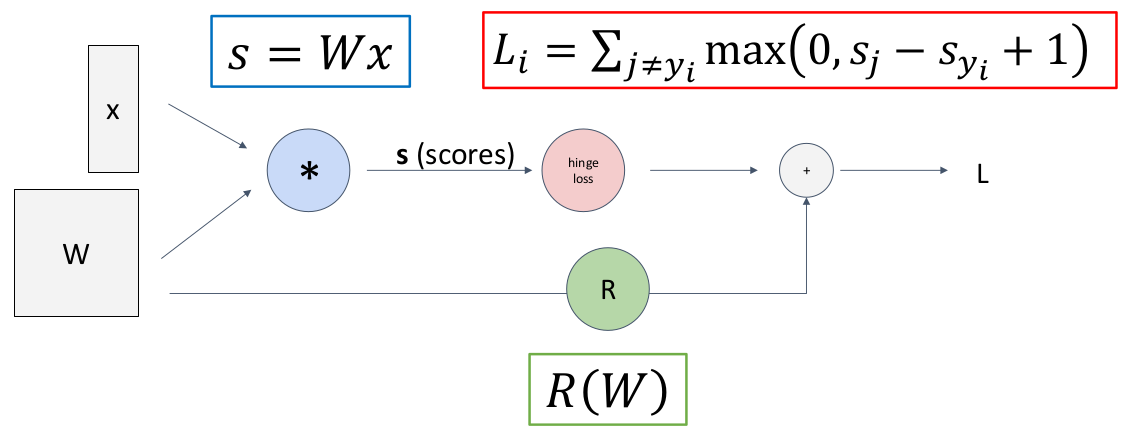
在计算图中,我们能够通过 “反向传播”(back-propagation)的方法计算输出变量关于输入变量的偏导数。例如对于
在计算图中按拓扑序的方向正向计算结果;
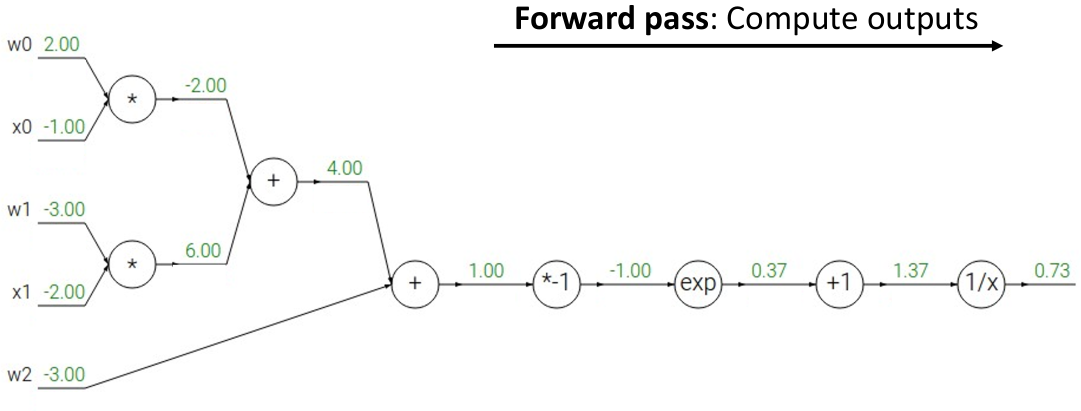
第一列代入计算得到损失结果后,从输出结点向前反向传播计算数值梯度。例如 upstream gradient 是
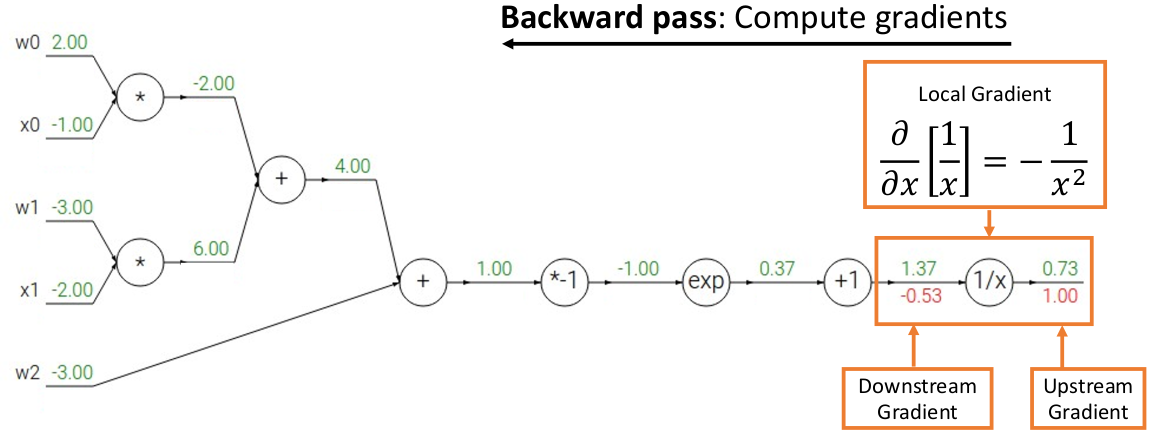
同理一直这样计算下去直到输入源结点,例如最后
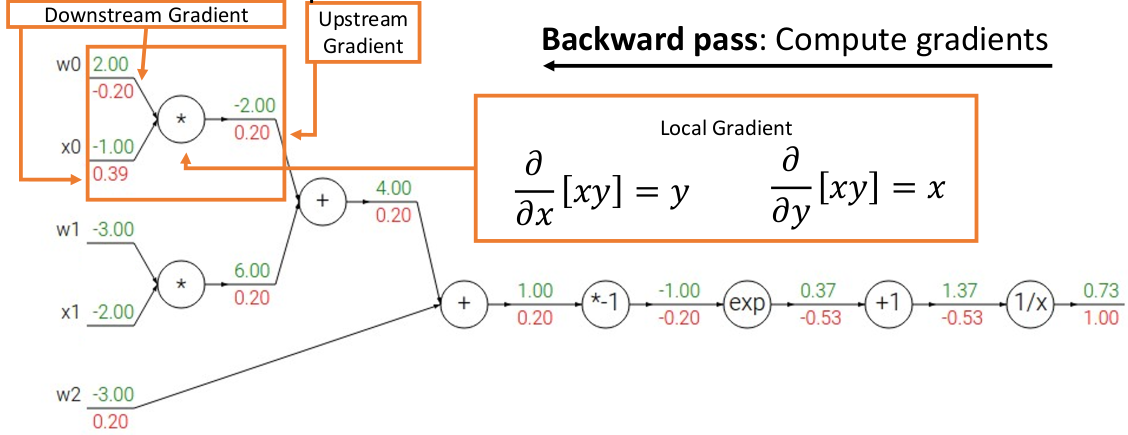
上面正向 + 反向传播算作完成一轮梯度下降迭代运算,我们可以将梯度代入梯度下降法的优化方法中优化参数,并重复直至达到 metrics 或者步数足够。
我们发现,对每个结点,只需要知道这个结点算子的偏导函数,即可快速地进行反向传播和代入运算,这在大规模计算时无疑非常方便。
再注意到一点,上面的函数恰好是 sigmoid 激活函数(参见 3.2)的一部分,而我们注意到,由于链式法则的性质,嵌套的函数也满足这个计算性质:
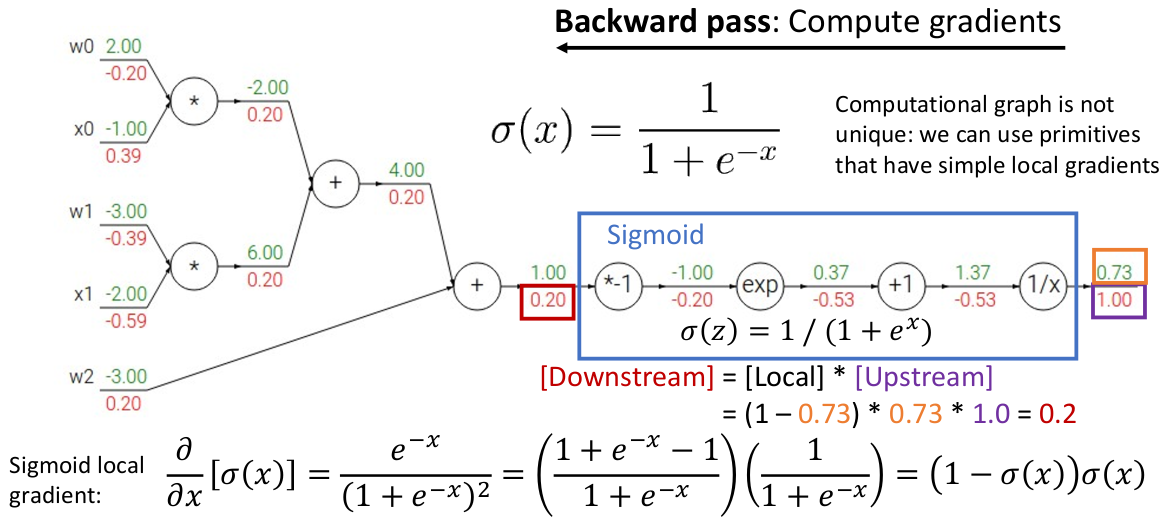
这就说明,一个模型的计算图并不是唯一的,我们可以用一系列已知的函数(尤其是像 sigmoid 这样方便计算导数的)作为积木(而不是最原始的运算符)进行反向传播,这就是计算图的算子优化。它能节省不必要的计算、极大地提升反向传播计算效率。
注意到 sigmoid 函数的导数非常非常容易计算,这也是为什么它被作为激活函数之一:既满足 “两头饱和、中间快速增长” 的阈值特性(符合网络计算需求),又容易计算(偏)导数。
现在我们了解了如何计算某个区域如何计算偏导数,我们现在形式化一下以便对于更普遍的结点进行计算。对于网络中的任意一个结点,从网络反向传播上游计算的 upstream gradient(如下例
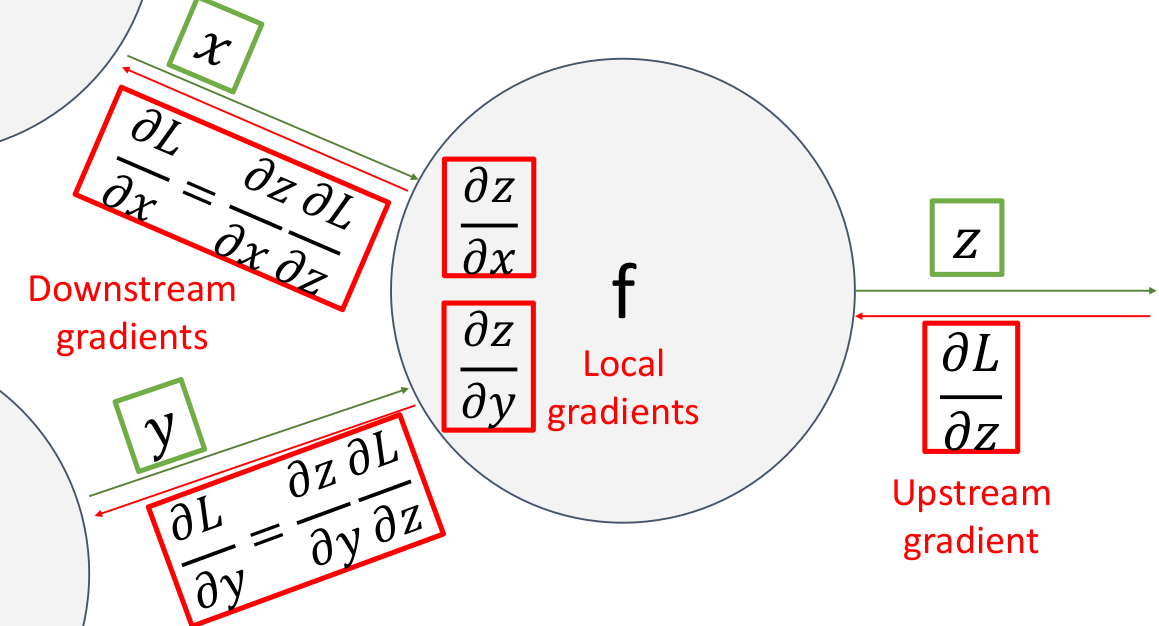
最终在反向传播结束后,计算图会得出损失函数关于所有输入变量的偏导数,这样我们可以用数值梯度信息对参数进行一轮训练迭代。
这样的计算方法可以让我们每次只关注一个局部的函数结构,而不需要关系系统全局信息,这非常利于进行大规模的并行计算。
3.5.2 Patterns in Gradient Flows
如果你理解了上面的计算过程,就能从直觉上领会到所谓反向传播就是,信息先从输入向前经过中间结点传播到输出位置,然后以相反的途径流回输入的位置,你就能发现这里有一些对偶性(duality)。我们将这个角度称为 “circuit perspective”。总结这些性质能帮助我们理解,这些计算图中的结点直观上究竟对梯度做了什么。
例如一个加法算子结点,无论它的输入参数有几个,由于偏导总是 1,因此它在反向传播梯度的时候,只是简单地将梯度复制给每个输入下游:
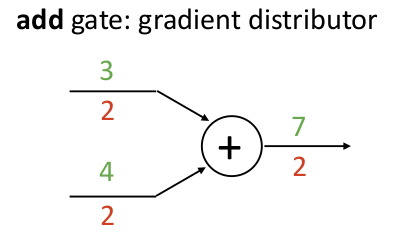
而对偶地,如果有一个算子是复制算子,只是将输入复制给后面的若干输出,那么在反向传播梯度的过程中,它就是将各个上游梯度累加起来!
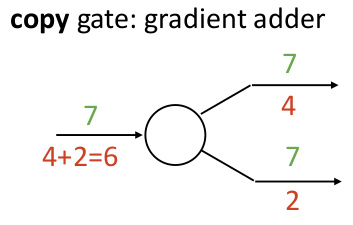
复制算子会在哪里用到?例如你需要进行正则化时,希望将输入同时传给正则化算子,以及网络的下一层。
于是我们称加法算子和复制算子是对偶的。
再来看一个乘法算子结点,由于乘法的关于某变量
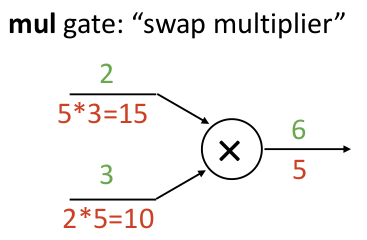
以及最大值算子结点,它表现成一个 “gradient router”,梯度只流向最大的输入那边,就像一个路由一样:
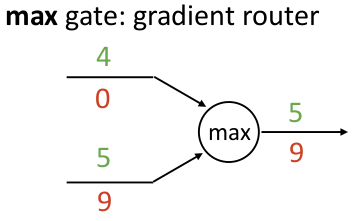
这就给了我们一些启发,例如,如果你的模型里面含有大量的 max 函数,可能造成反向传播时很多梯度都是 0,影响实际训练效果。
这也是人们在有些情况下使用 softmax 算子而不是 max 算子的重要原因之一!
3.5.3 How to Implement Back-propagation: "Flat" Gradient Code (Scalars)
代码上,我们如何实现上述的反向传播的计算?先从最 naive 的开始,我们仅仅将刚才总结出的反向传播的方法,针对特定的模型硬编码出来:
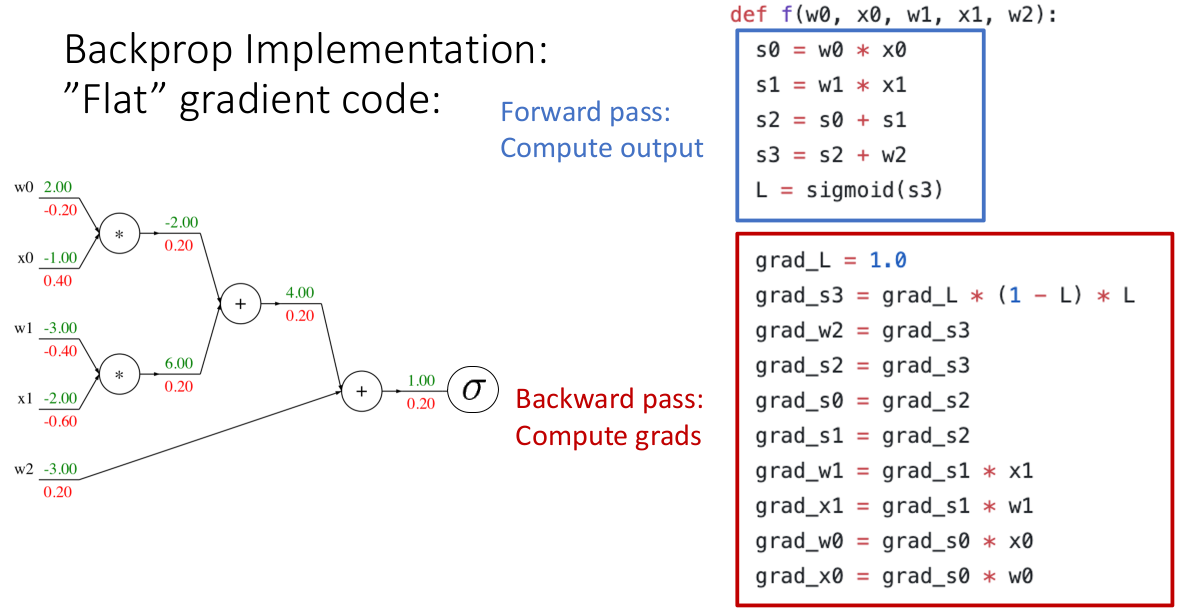
注意到,这就是利用了上面的计算方法,在正向计算的代码后反向计算一遍梯度。这个实现是正确的!你可以对着任意层神经网络使用这种方法。
但是这样做有个问题,它不模块化,一旦我们更改了模型结构、更换任意一个激活函数、更换任意一个正则项/损失函数,都需要重写代码。因此我们称之为最直白的实现。
3.5.4 How to Implement Back-propagation: Modular API (Scalars)
如果需要模块化,我们就需要为计算图准备一个类型,为每个结点也准备一个类型,并且实现它们的 forward 和 backward 时计算的方法。
这样得益于反向传播的模块化计算的特性,我们可以通过正向和反向遍历并执行计算图中的各个结点的 forward 和 backward 方法,就能计算出我们需要的梯度值。
事实上工业界的系统也是这么做的,例如 PyTorch 中,如果我们想在网络中定义一个算子结点,可以继承于 torch.audograd.Function 类型。比如一个标量乘法算子
xxxxxxxxxxclass Multiply(torch.autograd.Function): def forward(ctx, x, y): # context 是用于在网络传播计算时 stash 需要记忆 # 的数据,方便在反向传播时取出 ctx.save_for_backward(x, y) z = x * y return z def backward(ctx, grad_z): x, y = ctx.saved_tensors grad_x = y * grad_z # dz/dx * dL/dz grad_y = x * grad_z # dz/dy * dL/dz return grad_x, grad_y这个代码非常简单,完美描述了之前我们如何对神经网络计算图中的一个结点进行梯度反向传播的计算。
3.5.5 How to Implement Back-propagation: Vector-valued Functions
以上我们讨论的都是最简单的情况,对标量计算。如果我们希望网络能对向量(矩阵,或者张量)计算,有什么区别吗?
我们回忆一下向量微分、矩阵微分的相关知识。
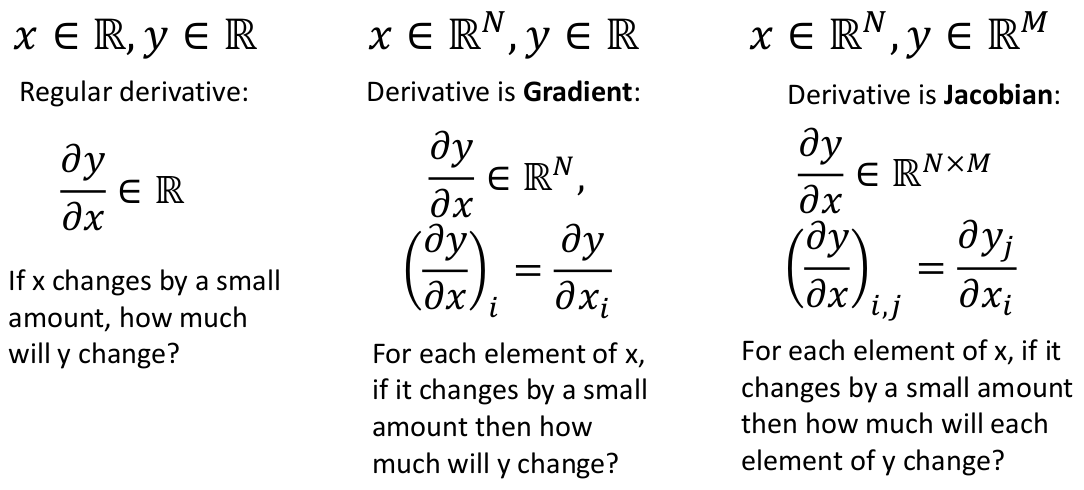
然后看一看,假如网络中每个算子计算的是向量,情况是怎样的。需要注意的是,损失函数的值仍然是标量!
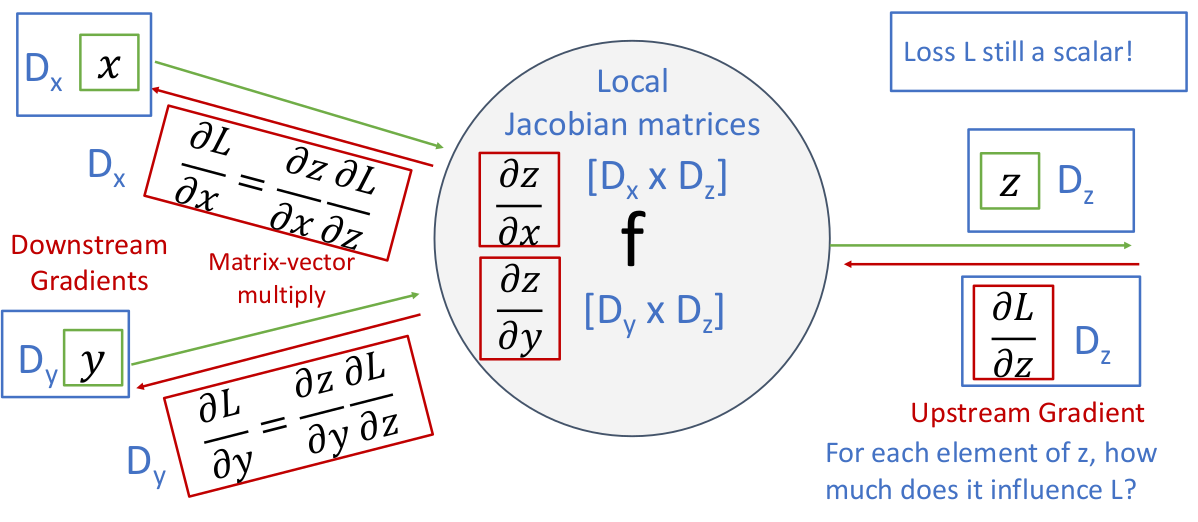
这个例子是一个两输入的向量函数
然后我们通过求
上面这张图就以
再举一个具体的例子,假设

其中的 Jacobian 矩阵表示其中输入向量单位变化会如何影响输出向量的变化(
事实上,这个例子中的 Jacobian 矩阵已经算密集的了。在大多数情况下,一个张量函数的 Jacobian 函数是非常非常稀疏的(尤其是维度很大的情况,每个元素越有可能统计学相互独立,再加上元素数量是维度数幂级增长的),因此我们不可能在实际应用时显式地构建 Jacobian 矩阵。幸运的是,对于 ReLU 函数,我们可以以解析式的方法写出它的 Jacobian 矩阵元素值:
我们仍然需要继续 generalize,因为实际应用的时候,神经网络需要能够以秩大于 1 的张量为操作数进行计算(例如矩阵、高维张量)。我们看看如果网络中每个参数都是矩阵/高维张量,情况是怎样的。
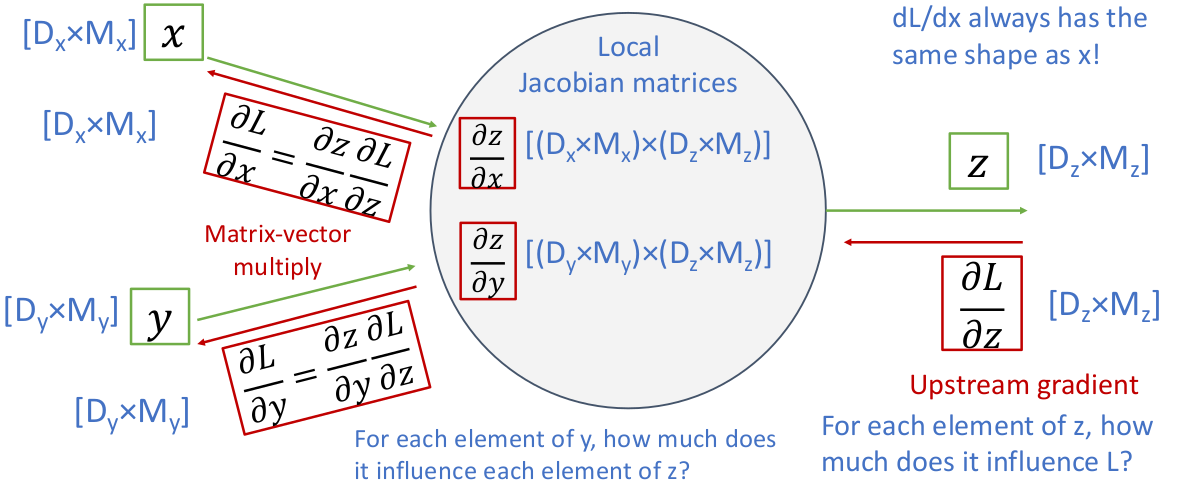
这个例子是一个操作数为矩阵(二维张量)的结点,输入
同理(参见向量推导)可知,
通过链式法则,我们有广义上的 “矩阵-向量乘法”(即高维张量和二维矩阵的乘法),同样可以得到 downstream gradients。
这种高维的操作如果再想画图画出来就困难了。我们需要想一种方法清晰地表述它,方便我们实现代码。
举个实际的例子:
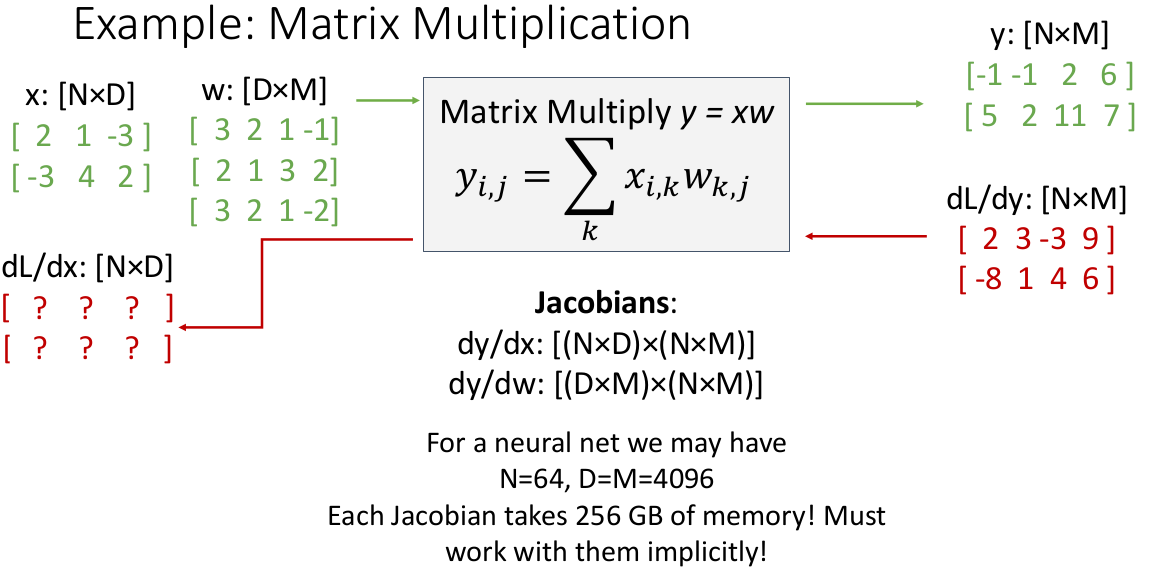
注意到这个 Jacobian 矩阵相当难以想象,我们就逐个 slice 构造,例如第一个元素就能快速解决:
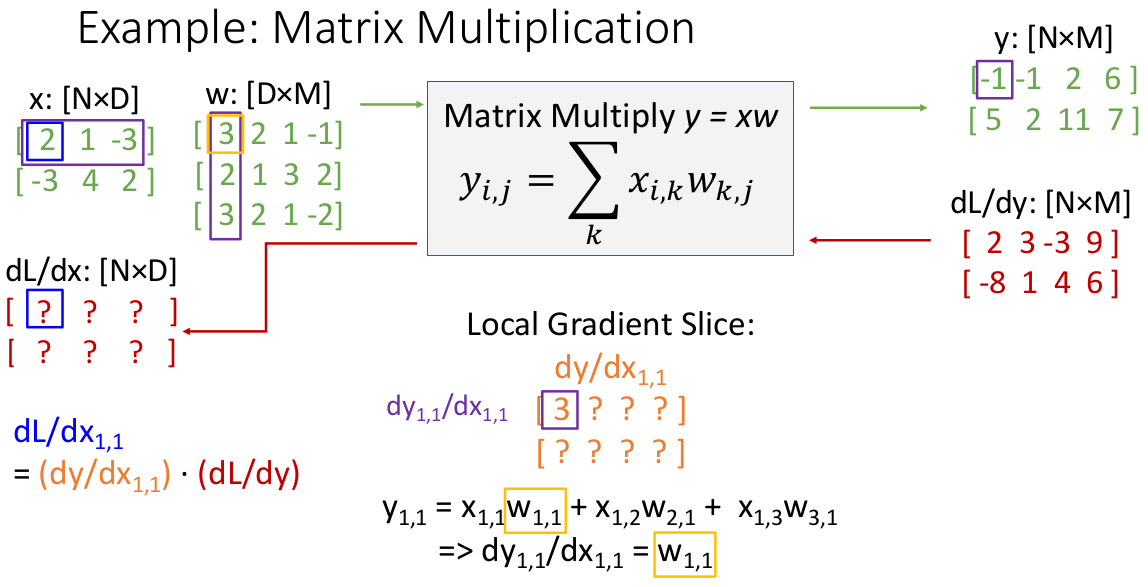
收集完成整个 : 是模仿 Matlab 和 NumPy 的取整行/列的写法):
掌握了一个元素的计算后,其余的都是重复,因此我们不需要理解 Jacobian 的整体样貌,就能归纳出整体计算公式了:
也就是说:
3.5.6 Reverse-Mode & Forward-Mode Automatic Differentiation
总结一下,我们将反向传播算法中的反向求微分的过程称为 Reverse-Mode Automatic Differentiation(反向自动微分)。这个反向算法非常精妙地避免了矩阵-矩阵乘法(请回想一下之前的运算过程),全是(广义的)矩阵-向量乘法,这通常有更高的效率。
拓展:如果有个系统输入标量,输出向量,想要求输出相对于输入的微分,这个时候,为了防止矩阵-矩阵乘法,我们需要 Forward-Mode Automatic Differentiation,也就是从前向后计算微分。
这在机器学习优化损失函数时基本不会见到,更常见的应用场景是物理引擎模拟计算。例如输入标量(如摩擦系数、重力等等),输出变化的物理向量。
因此 Forward-Mode 和 Reverse-Mode 这两种自动微分适用于很多需要机器求微分的计算场景,不仅仅是机器学习。
截止目前,PyTorch 2.6 已经放出了 beta 版本用于计算 Forward-Mode Automatic Differentiation,感兴趣可以尝试一下:Forward AD Usage - PyTorch;
3.5.7 Higher-Order Derivatives using Back-propagation
反向传播算法不仅仅能应对求梯度的场景,我们还可以利用它求高阶微分。
我们将向量计算图抽象成一如下过程(假设输入为
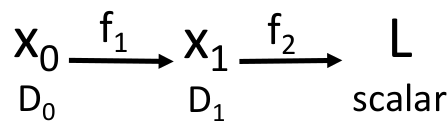
如果现在我们想知道
在有些情况下,我们需要在计算图中计算一个关于
这里为了利用反向传播算法,我们需要用到一阶微分的线性性:
当且仅当
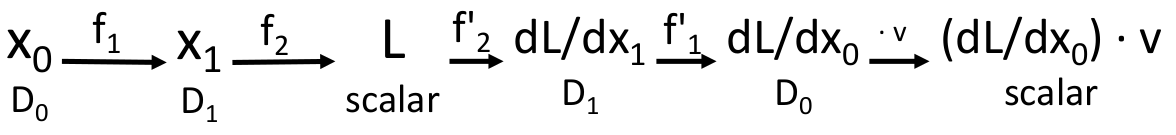
其中
这样我们可以使用同样的技巧计算任意高阶的偏导数,只要偏导 primitive operations(上面这些函数)的实现我们是知道的。
这个高阶偏导的算法在 PyTorch 和 TensorFlow 中都已经实现了。
再例如,一个我们可能需要的例子:
假设我们需要在计算图中定义一个正则项(这个特殊的正则项不是 L1/L2/Elastic Net,而是来自于一篇论文):
并且想知道
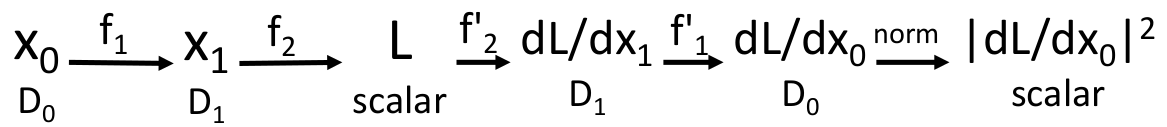
3.5.8 Conclusion
注意到,无论是线性分类器,还是反向传播算法支持的神经网络,它们在图像处理方面都有一个潜在问题:输入时总是将图像 flatten 为一维向量!这会丢失掉图像的空间结构和空间信息。因此我们可以继续优化网络结构:是时候了解卷积神经网络了!
Lecture 4. Convolutional Networks
4.0 Concepts
本章需要引入新的操作符:卷积层(convolution layers)、池化层(pooling layers)、正则化层。
考虑为了应对存在空间结构的输入,引入一个新的卷积计算方法:假设输入是一个 3 x 32 x 32 图像张量(深度为 3),引入 3 x 5 x 5 的 filter(之前的 weight matrix),并暂时假设 filter 的深度与输入图像的深度相同。
我们想象将 filter 沿着输入图像张量滑过,每经过一个重叠的位置时计算一次乘积(
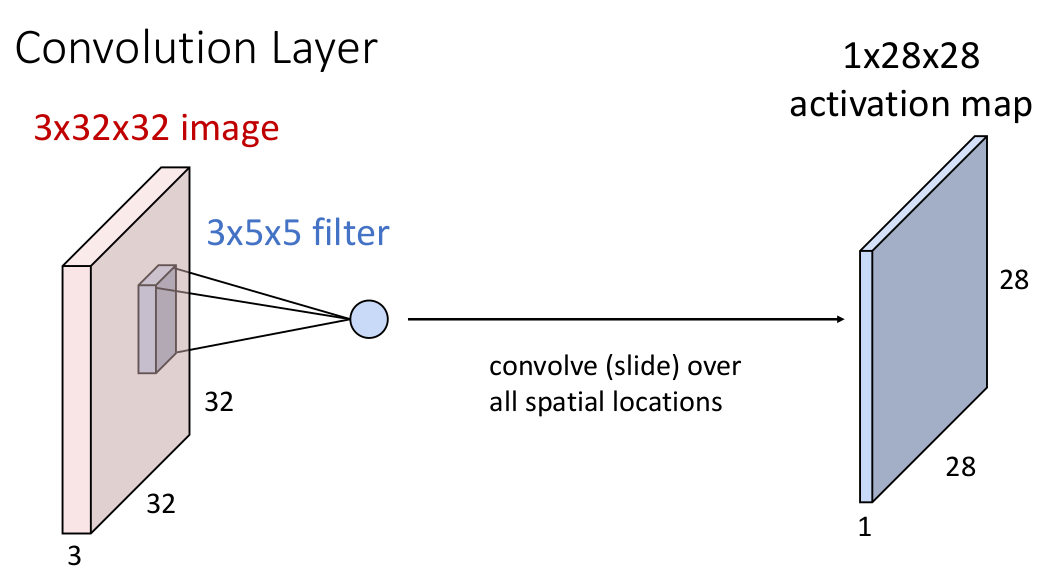
当然只有一个 filter 的信息是有失偏颇的,我们不妨重复 6 次(有点像多头注意力?),每次的
现在这个结果张量有两个理解方法:
6 个 activation map 的集合,每个代表了一个 filter 和输入图像的关系;
28 x 28 的网格,每个网格单元都是一个 6 维向量,描述特定位置的输入张量和 filter 组的数据关系;
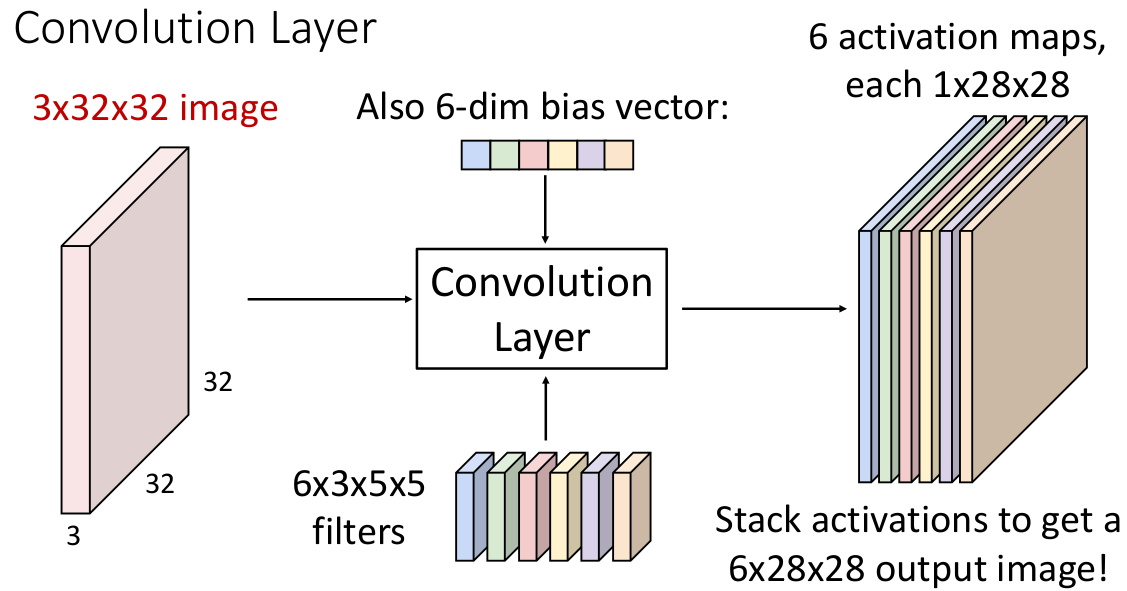
实际上在应用中我们会批量处理输入张量,假设每批 2 个,那么输入张量就能组成 4 维张量(2 x 3 x 32 x 32)。
现在拓展一下可以知道,一个 N 个输入张量(
filters 个数为
输出矩阵
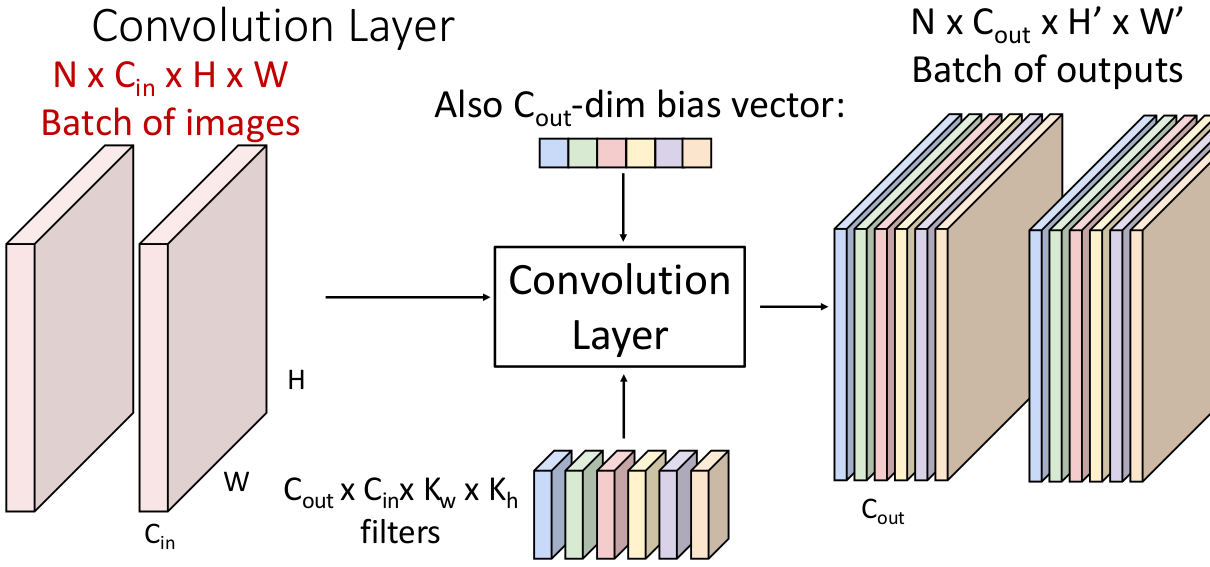
用数学方式表达:
考虑一个问题,我们能否像这样将卷积层叠加起来:
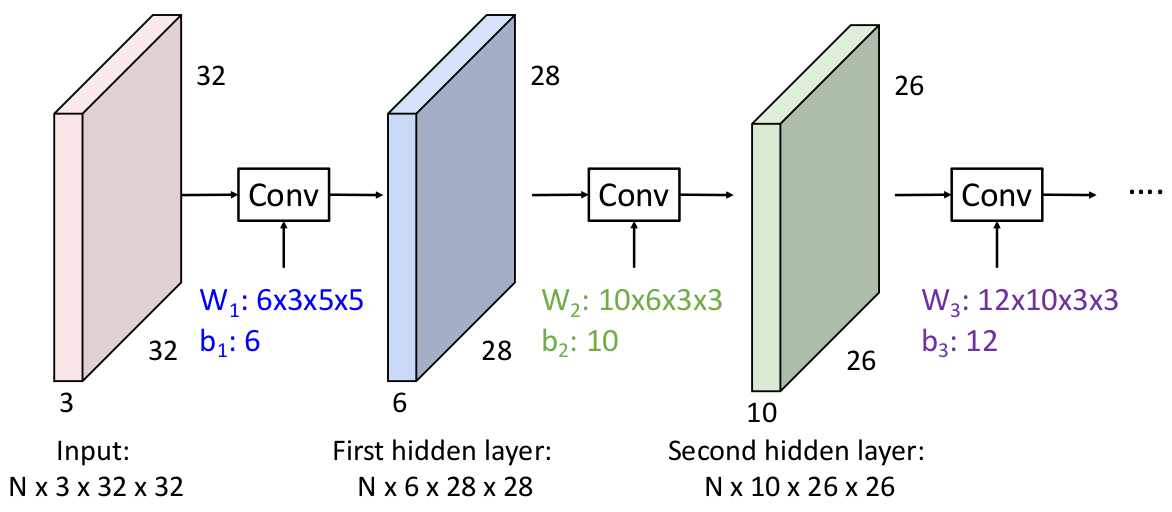
答案是不行,就像我们在构建全连接层组成的神经网络中遇到的,
因此我们需要在各层间加入激活函数(element-wise):
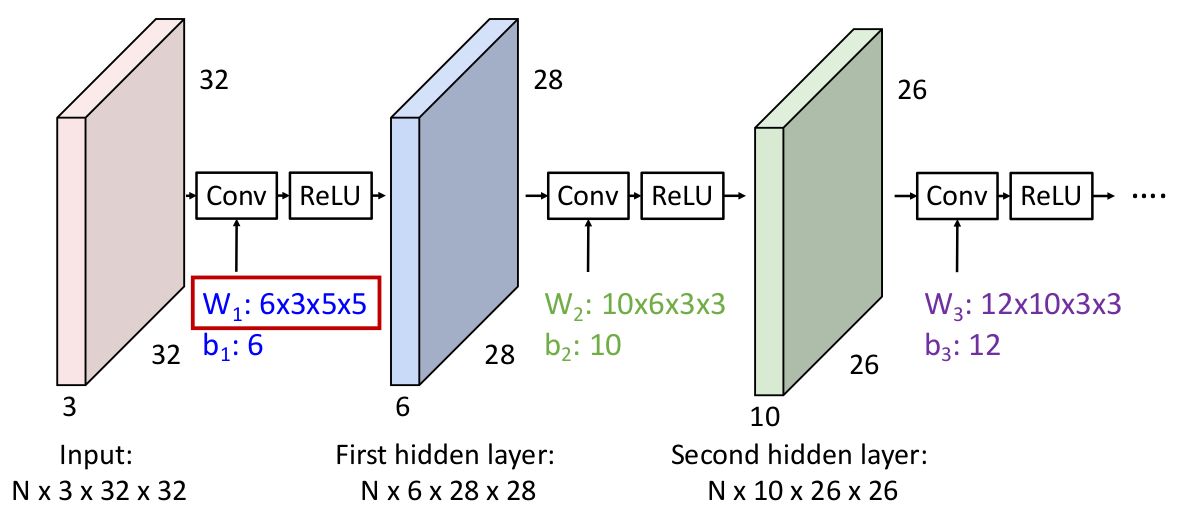
4.1 A Closer Look At Spatial Dimensions
4.1.1 Padding
我们先只考虑输入张量的某一个通道,很容易发现,每进行一次卷积操作,输出张量
这会导致:每经过一个卷积操作,feature map 的两个维度减小一定值,如果我们希望有多层卷积层而输入张量的维度并不足以支持的时候,就没法构建了(而且这需要考虑很多 corner cases)!
我们并不希望模型的层数受限于卷积层这样 “蒸发数据维度” 的特性。因此,人们为此引入了 padding,也就是在进行卷积层计算前,先在外围 padding 一圈 0 元素(假设 padding 的层数为
虽然
举个例子,下面是一个
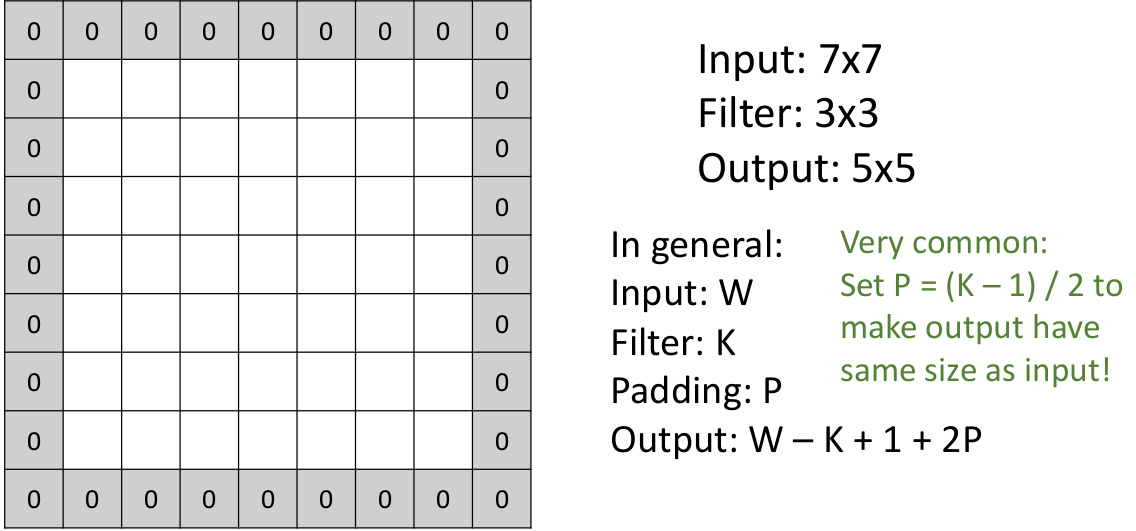
这是因为人们通常不想 spatial size 因为卷积操作随意变化,除非有意为止,或者有理由这么做。
考虑一下,zero padding 会不会向网络引入额外的数据或信息?
我们的本意并没有想向网络中增添信息,只是一种防止 shrinking 的手段。但是实际上确实引入了一些额外信息:它告诉了网络,filter 当前位于输入张量的什么位置。这会使得卷积操作是 Translation Equivariance(平移等变)的。
这种平移等变的性质会使得,如果 input tensor 平移一段距离后,output tensor 也会移动相同的距离。
等变是数学表述,函数
相对于函数 是等变的,当且仅当: ; 平移操作则是一种几何变换,它将所有点沿给定方向移动相同的距离,
;
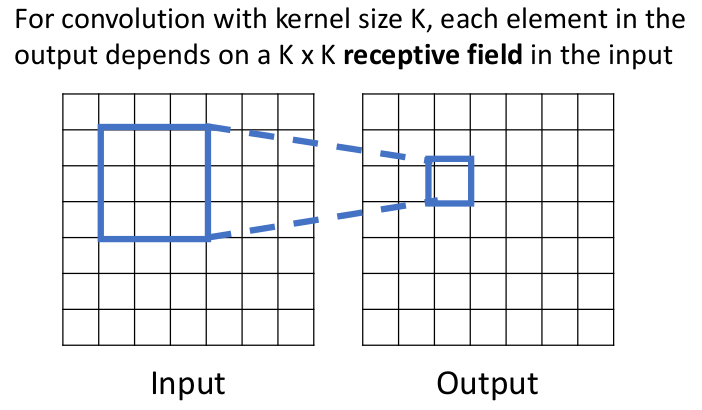
4.1.2 Receptive Fields
注意到,之前我们提到 feature map 的一种解释是,“每个网格单元都是一个
如下图,这是一个核的两个维度大小相同的特例:
如果在多层卷积层中,我们同样有感受区的概念,这能帮助我们理解数据信息的 “流动情况”:
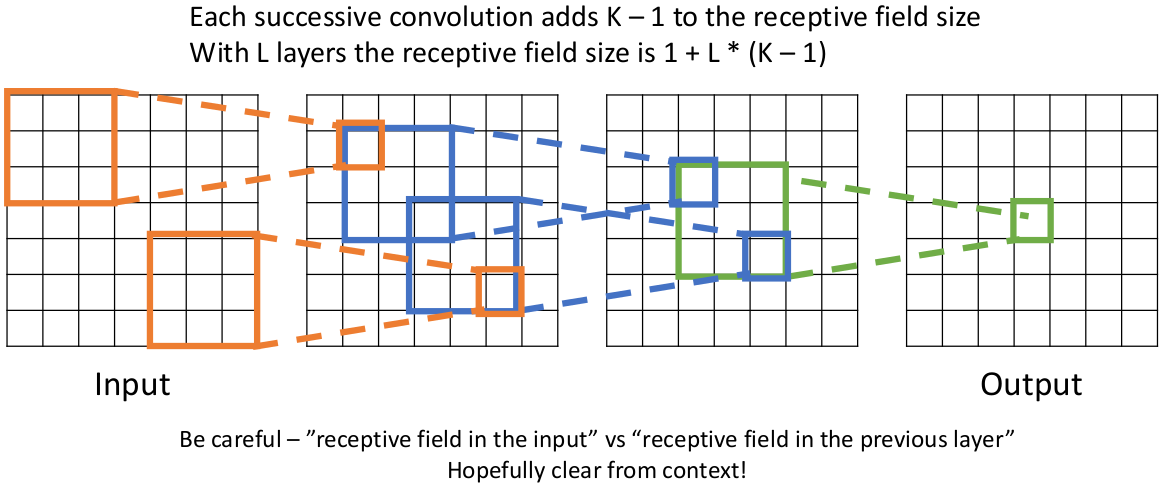
这告诉我们两件事:
在一个层数比较多的卷积神经网络中,深层张量的元素取决于 input tensor 中几乎所有的信息,这充分展示了卷积网络能够充分利用空间信息;
现在 receptive field 有第二个含义:一个 activation(activation map 中的一个元素)所对应的在 original input tensor 中能影响它的区域。
input tensor 中针对某个特定 activation 的有效的感受区大小,会随着卷积层的堆叠 线性增长。
这第二个点会有个问题:如果我们像解析一个解析度非常大的图像构成的张量,要想一个 activation 获取到足够全局的数据(最终让 feature map 的数据完全利用和依赖于输入的数据),就需要很多很多卷积层堆叠在一起,这是不现实的。
因为直觉上让 feature map 获取更多的 global context 会对模型的泛化性有好处。
我们的解决方案是,引入另一个超参数:stride。也就是 filter 扫描时每次前进两个元素单元。
现在输出 activation map 的形状和 input tensor 的关系是
common settings:设置 kernel size 各个维度相同、same padding(
);
例如输入一个 3 x 32 x 32 的 input tensor,使用 10 个 channel 相同的 5 x 5 filters,步长为 1,padding size 为 2,请问 activation map 的形状是怎样的?该层的可训练参数数量是多少?需要进行多少次 multiply-add 操作?
答:activation map 的形状是 10 x 32 x 32,可训练参数数量是 (3 x 5 x 5 + 1)*10 = 760。
注意到 activation map 中的每个元素都需要一次 3 x 5 x 5 的 element-wise 内积运算。计算为 768K 次 multiply-add ops;
研究表明 kernel size 1 x 1 的卷积层的行为和线性全连接层很像(都是将 “template vector” 单独作用于每个元素),但前者会改变 channel 数量,通常用在希望保留 input tensor 的空间结构、并且想调整 tensor 形状去适配其他层的时候。后者则会 flatten input tensor,通常用在网络的末端要生成 scores 的时候。
4.2 Other Dimensions
前面提到的都是 2D Convolution Layer,1D 卷积层通常做的操作像这样:
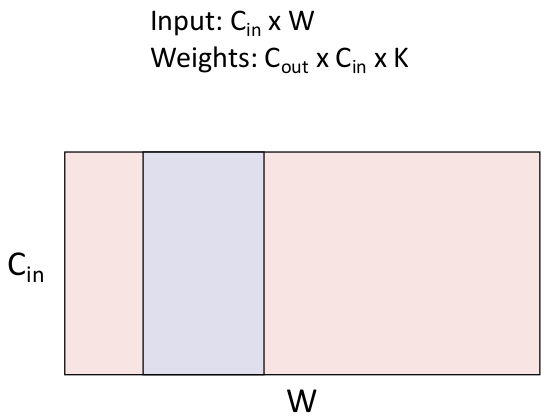
通常用在处理文本/音频数据(以序列的形式出现)的方面。
3D 卷积层则需要输入 4 维张量(包含 channels),
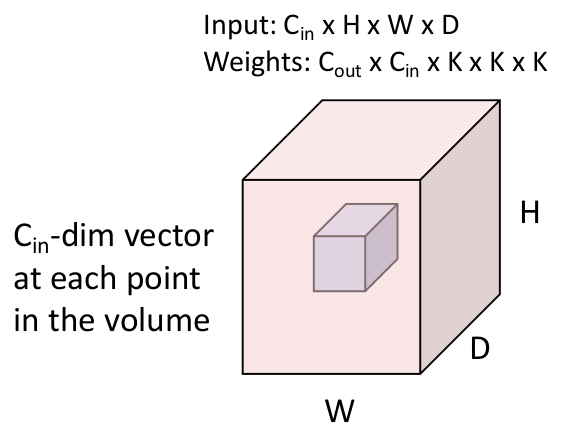
4.3 Pooling Layer
卷积神经网络中另一个重要的层是池化层,它的作用是 downsample(下采样),在不改变 channel 的情况下减小 input tensor 每个维度的大小(相当于将信息浓缩到更小规模的数据中)。
池化层不包含任何可训练参数,只有超参数 kernel size、stride 和 pooling function;
如何 “浓缩” 呢?我们考虑 pooling function。
Max Pooling
最大值池化方案,就是将最大值函数作为 pooling function,它的思想是选取每个 stride 对应的区域(pooling regions)中最大的元素来提取信息(比较一下一般的卷积层是做 element-wise inner product)。以 stride 为 2、kernel size 2x2 的情况为例:
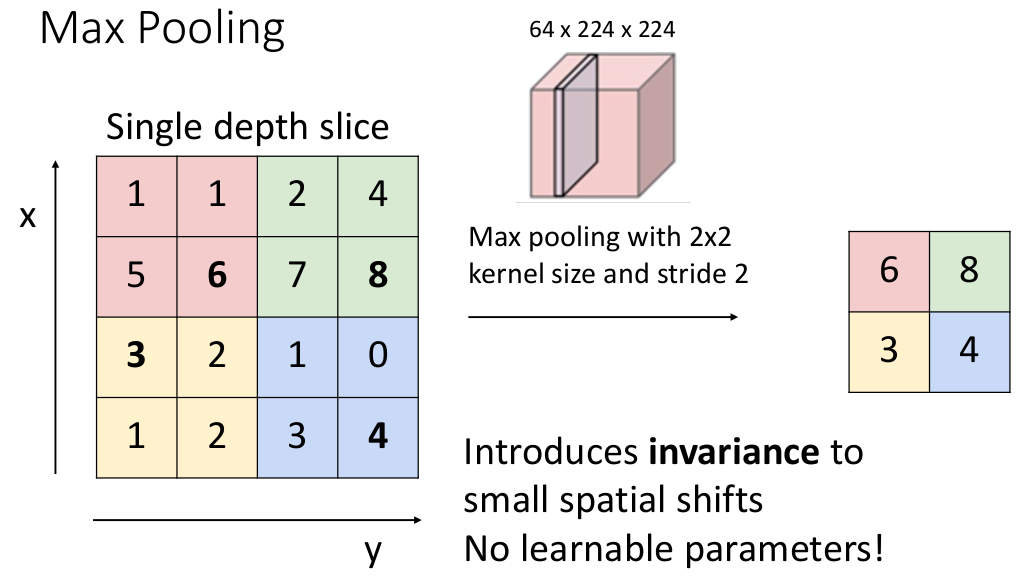
注意到如果 stride 和 kernel size 的维度长相等,则 pooling regions 不会互相 overlap。
能注意到 Max Pooling 引入了一些平移不变性的性质。
Average Pooling
如果 pooling function 是取平均的话就是平均值池化。
所以说池化反而是利用了卷积层 shrink 的特性,它不进行 inner product 运算,只是利用 pooling function “浓缩特征”。
总而言之,池化层可以提供如下作用:
降低空间维度(下采样)
通过减少特征图的分辨率(如从
[H, W]到[H/2, W/2]),显著降低计算量和参数量,防止过拟合。例如,最大池化(Max Pooling)或平均池化(Average Pooling)会保留局部区域的主要特征,同时丢弃冗余信息。
平移不变性(Translation Invariance)
池化操作对输入的小幅度平移、旋转或形变具有鲁棒性。例如,最大池化会保留区域内的最大值,即使目标位置略有偏移,输出仍可能保持一致。
特征抽象和泛化
通过逐步压缩空间信息,网络更关注高层次语义特征(如“猫耳朵”或“车轮”),而非低层次细节(如像素位置)。
问:池化层是一个非线性层,使用它就可以不需要 ReLU 激活函数了?
理论上是的,但实际
但是也可以被普通卷积层替代:
计算资源充足:如果对计算效率不敏感,可用步长卷积或更深的网络替代池化层;
需要高分辨率特征图:如语义分割任务中,需保留细节信息,可能避免池化层(或用空洞卷积替代);
数据量极大:若数据足够多,网络可能通过步长卷积自动学习到类似池化的特性(但需牺牲一定效率或依赖更多数据训练);
4.4 Classic Convolutional Networks
一种比较经典的网络设计方式是,使用 (卷积层 + ReLU 激活函数 + 池化层) * N -> flatten -> (线性全连接层 + ReLU 激活函数) * M -> 线性全连接层 (输出 scores)。例如 LeNet-5 网络:
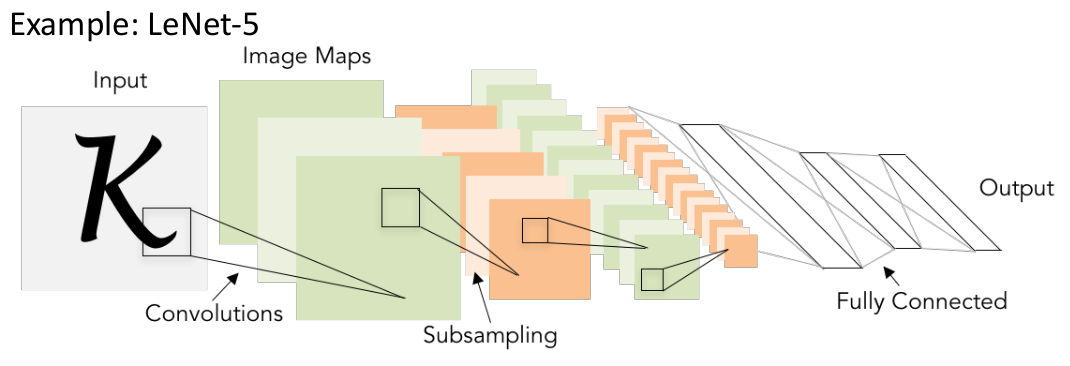
spatial size decreasing + depth channel size increasing;
同样的问题是,这样深层的网络会很难训练(优化)。