Modern Compiler Implementation in C
Modern Compiler Implementation in CChapter 0. Concepts & Principles0.1 Modules and Interface0.2 Example: Straight-line Program LanguageChapter 1. Lexical Analysis1.1 Tokens & Lexemes1.2 正则表达式1.3 正则 与 词法表示1.4 Finite Automata1.4.1 Concepts1.4.2 Regular Expression to NFA1.4.3 NFA to DFA1.4.4 DFA to Table1.4.5 The Execution Rule of a DFA1.5 Lex: The tool to generate DFA C code from R.E.1.5.1 Format of the Input File: *.lexDefinitions SectionRules SectionComment in Rules FileRegular Expressions (Pattern) in Rules FileActions in Rules FileStart Conditions (Mini Scanners)Member Functions in Flexc++'s Output Class Scanner1.6 Lexical in Tiger LanguageChapter 2. Grammar Analysis2.1 Background2.2 Context-Free Grammar2.2.1 Production2.2.2 Derivation2.2.3 Parse Tree, Ambiguous Grammar, EOF2.2.4 Disambiguation2.3 Top-down Parsing2.3.1 Recursive Decent ParsingExampleLeft-Recursive GrammarConclusion2.3.2 Predictive ParsingLL(k) GrammarsExampleLeft-Factored & LL(1) LanguagesLL(1) Parsing Process: ExampleHow to Construct a Predictive Parsing TableError HandlingSummary2.4 Bottom-up Parsing2.4.1 Shift-Reduce Parsing2.4.2 LR(k) Parsing & DFA2.4.3 LR Parsing Algorithm2.4.4 Constructing LR Parser DFA2.4.5 Problem I in LR Parsing Table: Shift/Reduce Conflicts2.4.6 Problem II in LR Parsing Table: Reduce/Reduce Conflicts2.4.7 Optimization: LALR(1)2.4.8 LR(1) Error HandlingLocal Recovery & Delete TokensGlobal Recovery2.5 Yacc: The tool to generate parsing table from CFGChapter 3. Semantic Actions & Semantic Analysis3.1 Where we are now?3.2 Semantic Rules, Attribute Grammar, Abstract Syntax Tree3.3 Synthesized Attributes & Inherited Attributes3.3.1 Semantic Actions in Bottom-Up Evaluation3.3.2 Semantic Actions in Top-Down Evaluation3.4 Example of Semantic Action: The AST of Tiger Language3.4.1 What about Error Positioning?3.4.2 Tree Node Types3.4.3 Symbolic Table & Nested Function3.EX Bison: The tool to generate AST from SDD3.EX.1 Bisonc++ Directives3.EX.2 Grammar Rules3.EX.3 Basic Grammatical Constructions3.EX.4 The Generated Parser Class' Members3.5 Semantic Analysis3.5.1 Scope Information, Binding Information, Environment3.5.2 Implementation of a Environment TableImperativeFunctional3.5.3 An Example: Bindings in Tiger Language3.5.4 Another Example: Type-Checking in Tiger LanguageImplementation ExamplesAbout Recursive Definitions (Self & Mutual)Name or Structural EquivalenceType ConversionGeneral OverloadingChapter 4. Translations4.1 Activation Records4.2 Registers & Frames Allocation4.2.1 Function FramesCall-by-ValueCall-by-ReferenceCall-by-RestoreFunction: Call-by-Name4.2.2 Function Parameter Passing4.2.3 Variable-Length Argument List4.2.4 Frame-resident Variables4.2.5 Global Variables4.2.6 Heap Variables4.3 Example for Tiger: Static Link4.4 Language Frame & Escape Analysis4.5 Introduction to LLVM IR4.5.1 Basic Concepts4.5.2 LLVM IR BuilderOverviewType System in LLVM IR & Its BuilderLocal Variable Management of LLVM IRGlobal Variables Management of LLVM IRLLVM IR InstructionsHow to Write A LLVM IR Builder From Scratch?4.6 In-Frame Variable Management4.7 Translation Implementation: To LLVM IR4.7.1 Definitions4.7.2 An Example for Tiger Language如何处理数组、结构体?左值 和 右值?4.7.3 Memory Safety4.7.4 Translate Arithmetic4.7.5 Translate Conditionals4.7.6 Translate Logical Expression4.7.7 String Creation4.7.8 Record & Array Creation4.7.9 Loop Translation4.7.10 Function Translation4.7.11 Declaration TranslationChapter 5. Instruction Selection5.1 Theories: Jouette Architecture & Selection Methods5.2 Practice I: LLVM-based Instruction Selection5.3 Practice II: Instruction Selection for the Tiger Compiler5.3.1 Targets & PreparationsGenerate Register NumbersInstruction WrapperBB Jump WrapperDe-duplicate LabelsCode Generation Wrapper in Frame LevelFunction Entry/ExitNo Frame Pointer in TigerRegister Mappingtemp::Temp Mappings%my_sp Management5.3.2 Generate from LLVM Instructionsllvm::Instruction::Loadllvm::Instruction::Add/Sub/Mul/SDivllvm::Instruction::Callllvm::Instruction::Retllvm::Instruction::ICmpllvm::Instruction::Brllvm::Instruction::PhiOther InstructionsChapter 6. Local & Global Optimizations6.1 Preparations6.1.2 Definition: Local Optimizations6.1.3 Definition: Global Optimizations6.2 Global Analysis6.2.1 Example: Liveness Check6.2.2 Forward & Backward Analysis: Constant Propagation as an Example6.2.3 SummaryChapter 7. Register Allocation7.1 Problem Definitions7.2 K-Coloring & Approximation7.3 Optimization: Register Coalescing7.4 Misc: Architecture Conventions & Pre-colored Nodes7.5 Corner Case: Caller Registers7.6 Put it Together: A Complete Example7.7 Too Many Spilling Registers?7.8 R.A. Implementation in Tiger CompilerChapter 8. Garbage Collection (GC)8.1 Problem Definition8.1.1 Why & How8.1.2 GC Metrics8.2 Mark & Swap8.3 Reference Count8.4 Copy CollectionOptimizations?8.5 General Collection (Generations)8.5.1 Design8.5.2 Patch: Ways of Remembering8.6 Incremental Collection8.7 Concurrent Collection8.8 GC Interface in Compiler8.9 Example: Modern GC in JavaChapter 9. Functional Programming Languages9.1 Closure9.1.1 Why?9.1.2 Implementation9.2 Pure Functions & Immutable Variables
Chapter 0. Concepts & Principles
0.1 Modules and Interface
对于任何大型软件系统,如果设计者注意到了该系统的基本抽象和接口,那么对这个系统的理解和实现就要容易得多。
编译器就被分解成不同的部分(分别称为 “阶段” 和 “接口”):
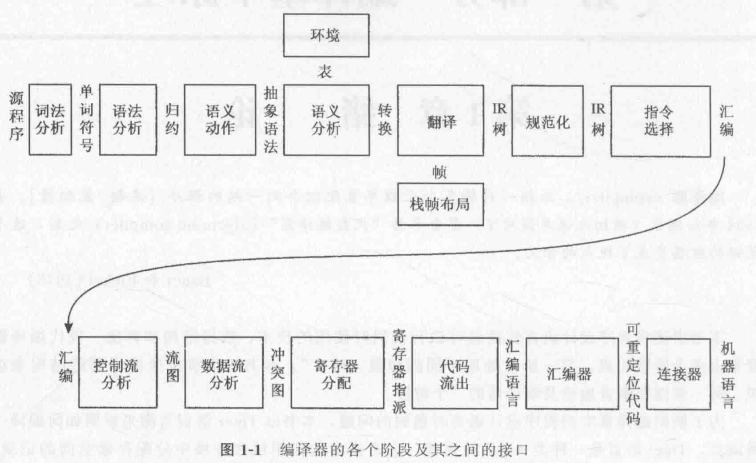
词法分析(Lexicon Analysis):将源文件分解为一个独立的单词符号(token);
语法分析(Grammar Analysis):分析程序的短语结构;
语义动作(Semantic Action):建立每个短语对应的抽象语法树(AST);
语义分析(Semantic Analysis):确定每个短语的含义,建立变量和其声明的关联(表),检查表达式的类型,翻译每个短语;
栈帧布局(Frame Layout):按机器要求的方式将变量、函数参数等分配于活跃记录(即栈帧)内;
翻译(Translation):生成中间表示树(IR Tree);
这是一种与任何特定程序设计语言和目标机体系结构无关的表示;
规范化(Normalization):提取表达式中的 side effects,并且整理条件分支,方便下一阶段处理;
指令选择(Instruction Selection):将 IR Tree 结点组合成与目标机指令的动作相对应的块;
控制流分析(Control Flow Analysis):分析指令的顺序并建立控制流图(Control Flow Graph)。此图表示程序执行时可能流经的所有控制流;
控制流分析可以帮助流程优化,例如死代码删除;
数据流分析(Data Flow Analysis):收集程序变量的数据流信息。例如,活跃分析(Liveness Analysis),计算每一个变量仍需使用其值的地点(即它的活跃点);
活跃分析可以帮助变量的优化;
寄存器分配(Registers Allocation):为程序中的每一个变量和临时数据选择一个寄存器,不在同一时间活跃的两个变量可以共享同一个寄存器;
在 ICS 中提到,这是编译器需要做的非常重要的事;
代码流出(Code Output):用机器寄存器替代每一条机器指令中出现的临时变量名;
这样分解成多个阶段对编译器的好处是,能够尽可能重用它的组件。
例如,想要编译器生成针对于不同平台的 output,只需要更改栈帧布局(Frame Layout)和指令选择(Instruction Selection)这两个部分就行。
再例如,想要编译器编译不同的源语言,则只需要改变 “翻译” 模块以及之前的部分就行。
至于这些接口的用处:
抽象语法(Abstract Syntax)、IR 树、汇编(Assem)之类的接口,是以数据结构的形式做规约,方便下一阶段的实现;
另一些像 翻译接口、单词符号(token),是以数据类型的形式做规约;
其中,现代编译器两种最有效的抽象分别是:
上下文无关文法(Context-Free Grammar):用在语法分析,理解为 “形式化描述一个编程语言的语法规则,不涉及任何具体过程”;
正则表达式(Regular Expression):用在词法分析,理解为 “形式化描述一个编程语言合法的单词符号(token)”,现在已经被广泛应用到多个领域,例如 Web 前端的输入校验、文字匹配、IDE 高亮和提示等等;
0.2 Example: Straight-line Program Language
在正式学习编译理论前,我们简单地热个身。
先讨论一类最简单的语言:直线式程序语言。这类语言只有一般语句和表达式,没有循环和分支判断语句。
我们用形式化的文法规则来描述它的语法(理解成广义的上下文无关文法):
语句文法(statement):
Stm -> Stm; Stm,即:一个语句可以是另外两个语句以 semicon(结束符)分隔组成(执行顺序从左到右),称CompoundStm;Stm -> id := Exp,即:一个语句可以是一个赋值语句(作用域内唯一合法标识符id、一个表达式,执行顺序先Exp后赋值),称AssignStm;Stm -> print( ExpList ),即:一个语句可以是输出语句(print关键字 token、一个表达式列表,输出顺序从左到右),称PrintStm;
表达式文法(expression):
Exp -> id,即:一个表达式可以是仅仅一个标识符的陈列,称IdExp;Exp -> num,即:一个表达式可以是仅仅一个合法数字 token,称NumExp;Exp -> Exp Bionp Exp,即:一个表达式可以是两个表达式间用二元运算符连接(执行顺序先左后右),称OpExp;Exp -> (Stm, Exp),即:一个表达式可以是一个语句和一个表达式的组合的序列(以逗号分隔,先执行左边的语句,再执行右边表达式),称EseqExp;
表达式列表文法(Expression List):
ExpList -> Exp, ExpList,即一个表达式列表可以由一个表达式和另一个表达式列表组成(逗号分隔),称PairExpList(递归定义);ExpList -> Exp,即一个表达式可以仅由一个表达式构成,称LastExpList(递归定义终止);
二元运算符文法(Binary Operator):
Binop -> + or - or * or /,即一个二元运算符只可以是+,-,*,/其中一个;
Chapter 1. Lexical Analysis
1.1 Tokens & Lexemes
一种语言(language)是字符串(string)组成的集合。而字符串是 符号(symbol)的有限序列。而符号则来源于这个语言所定义的有限字母表(alphabet);
Lexeme:它是一种语言的字符串子串,由一串字符构成(抽象概念),是语言的基本单元。例如在一段代码中,if、10、+ 等等,都是 lexeme;
Token:一种语言对于 lexeme 的抽象的分类表示,可以将其看作程序设计语言的文法单位。token 可以归类为有限的几组单词类型(称 token type),例如 ID、KEYWORD、RELATION、NUM、REAL 等。它通常使用 (token-type, token-value) 对表示。
点符号、操作符、分隔符等也算 token;
例外:注释、预处理指令、宏、空格符/指标符/换行符等空白字符不是 token;
其中,IF / RETURN 等由字母字符组成的单词称为保留字(reserved word),在多数语言中,它们不能作为标识符(ID)使用。
二者的比较如下:
| Aspect | Lexeme | Token |
|---|---|---|
| Definition | A sequence of characters forming a basic unit of a language. | An abstract, categorized representation of a lexeme. |
| Representation | Concrete string (e.g., 123, if, +). | Abstract pair: type + value (e.g., (NUMBER, "123")). |
| Role | The actual text or code input. | The classified, processed unit passed to the parser. |
| Generated by | Directly from the source code or text. | Lexical analyzer/tokenizer converts lexemes into tokens. |
而实现一个词法分析器(Lexical Analyzer)就是在完成以下的工作:
扫描输入的内容,识别其中某些子串(lexeme)为 token;
返回一组 (token type, token value) 对;
这个过程被称为 Tokenization;
举例:对于下面的一个语句:
int num = 10;
int、num、=、10、;都是 C 语言的 lexeme;tokenization 的过程:
Lexeme
int-> Token(KEYWORD, "int");Lexeme
num-> Token(IDENTIFIER, "num");Lexeme
=-> Token(OPERATOR, "=");Lexeme
10-> Token(NUMBER, "10");Lexeme
;-> Token(SEPERATOR, ";");这个过程就是词法分析器需要做的事。
为了定义一类 token 的规则,我们引入正则表达式来描述这套词法规则。
1.2 正则表达式
一种形式语言,formal language,被广泛使用的最弱的形式语言(the weakest formal language);
Atomic RE:
Single Character: L('c') = ["c"];
Epsilon:
Concentration: L(AB) =
Union: L(A | B) =
Repitation:
1.3 正则 与 词法表示
从现在开始,我们以一种新定义的语言 Tiger 为例。我们使用正则表达式来定义 Tiger 的词法。
例如 Tiger 的 Token 就可以这么定义:
KEYWORD:
"else" | "if" | "let" | "var" | "type" | "for" | "function" | "do" | "while" | "then" | "end" | ...;NUMBER:
[0-9]+(某些编程语言的 re 库中表示为\d+);ID:
[a-zA-Z_][a-zA-Z_0-9]*;WHITESPACE:
(' ' | '\t' | '\n')+(re:\s);LEFTPAR / RIGHTPAR:
'('/')';OPERATORS:
'+' | '-' | '*' | '/';……
可能有些 Lexeme 符合多种 token 的定义,因此会规定 token 优先级。
规定了一种语言的词法,接下来要考虑的是如何实现。那么如何实现正则表达式?答案是采用一种特殊的数据结构:有限自动机(FA)。
总体路径如下:
RegExp -> NFA -> DFA -> Tables;
1.4 Finite Automata
1.4.1 Concepts
定义:有限状态机(FA)是一个包含有限个元素(作为 “状态节点”),以及元素间转移的有向边的 图数据结构。
特征:有限自动机有一个有限状态集合和一些从一个状态通向另一个状态的边,每条边上标记有一个符号;其中一个状态是初态,某些状态是终态。
其中,确定有限自动机(Deterministic Finite Automata,DFA)是有限自动机的特殊情况,它不会有从同一状态出发的、两条或以上标记为同样符号的 边,这种有限自动机称为 “确定有限自动机”,意为:“根据输入情况和当前状态一定能确定下一状态” 的有限自动机。
相反地,有不确定有限自动机(Nondeterministic Finite Automata,NFA);
运行逻辑:从初始状态出发,对于输入字符串中的每个字符,自动机都将沿着一条确定的边到达另一状态,这条边必须是标有输入字符的边。
对 n 个字符的字符串进行了n 次状态转换后,如果自动机到达了终态,自动机将接收该字符串。若到达的不是终态,或者找不到与输人字符相匹配的边,那么自动机将拒绝接收这个字符串。
对于 NFA,针对同一个输入可以对应多个状态(同时位于多个状态),在输入结束后,只要存在一个状态位于终态,那么就会接受这个输入。
根据自动机的运行逻辑,我们可以将一个正则表达式转换为一个 DFA / NFA,以此实现正则表达式的行为。
如果转换为 NFA,则虽然转换过程简单,但运行过程可能出现状态爆炸的问题;
1.4.2 Regular Expression to NFA
可以按照下面的算法将 RE 转换为一个有头有尾的 NFA;其中 “头” 为末端状态,“尾” 为开始边。
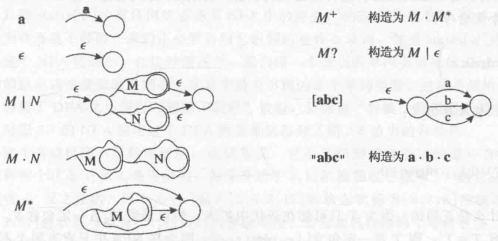
思考:
答案是,如果表达式只有
1.4.3 NFA to DFA
转换算法的主要规则如下:
实际上转换的过程就是模拟 NFA 的过程,DFA 中每个状态都是 NFA 状态节点的非空真子集;
创建 DFA start state:从 NFA 入口通过
创建转换过程(transition)
值得注意的是,转换的时候可能存在优先级关系,因此引入 Priority Rule:
假设正则表达式为
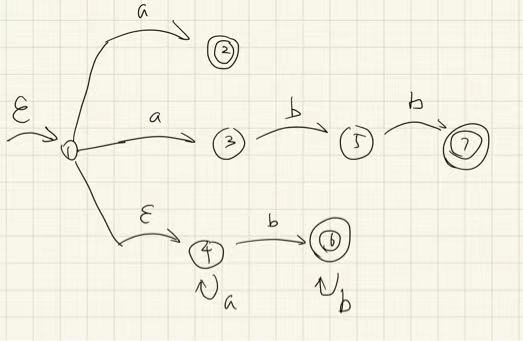
注意到优先级应该是 2 优于 7 优于 6(根据在正则式中的先后顺序);
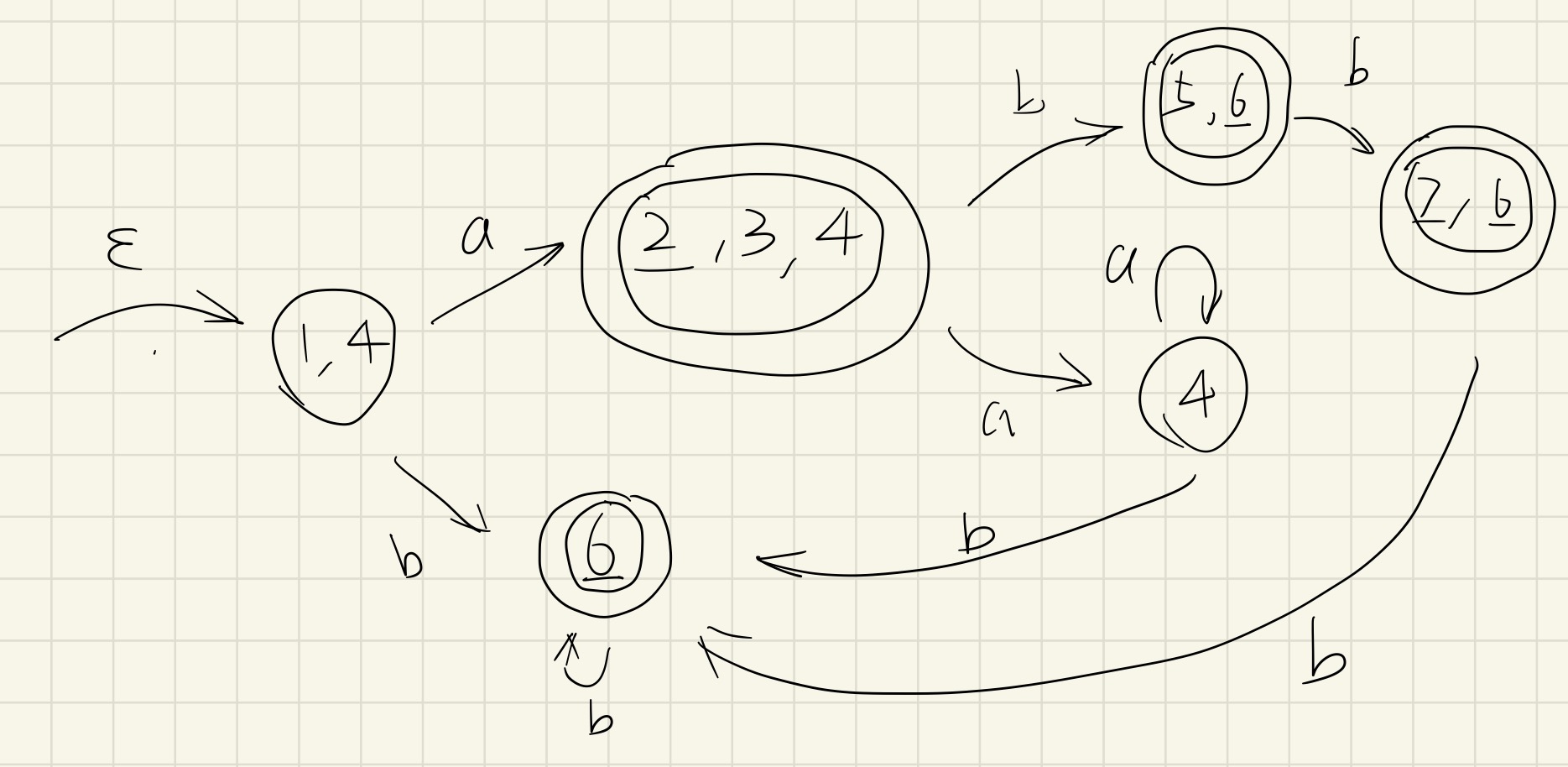
只要我们再加入下面的转换技巧,就能保证优先级:
在创建转换过程中,建议逐一考虑
建议使用 BFS 的方法创建转换过程;
在创建转换过程中,如果某个状态是终态,则在它的状态号下方标记下划线(方便识别),
一个
如果
最终 DFA 执行是停在非终态 / ERROR 终态,则解析错误;停在正确的终态中,从左到右(遵循优先级)考虑有下划线的状态编号,作为解析的结果。
1.4.4 DFA to Table
一个 DFA 可以被表示为一张 2D 的表格。其中一维存放所有 states,另一位存放所有可能的 Symbols,数学表达为
这样能方便计算机执行一个 DFA:通过查找
例如:
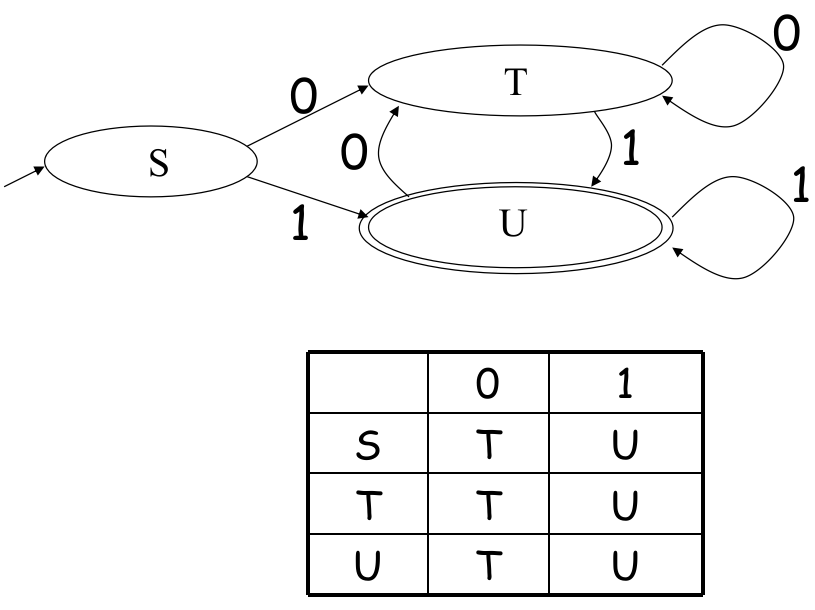
1.4.5 The Execution Rule of a DFA
首先明确三种标记:

给定几个规则:
初态时,三种标记(分别记为 IPLF、CIP、BCL)都位于第一个位置;
接受输入时,current input position(记为 CIP)向前移动、更新当前状态(一般使用 state ID 数字);如果移动后的状态是终态,那么也将 “input position at the last final”(记为 IPLF)移动到该位置;
当输入符号不在 DFA 的当前状态的出路径中 / EOF,总之是无路可走时,则立即检查 IPLF 所处的最终状态(可以是有效,也可以是 Error);
如果正确,则取得 BCL 到 IPLF 间的字符为一个 Lexeme,并返回;
如果错误,则输出错误信息;
无论是正确还是错误,解析完这个 lexeme 后,立即更新 BCL、CIP 到 IPLF 的位置,将当前状态重新置为状态机的初始位置;
如果在重置之后立即遇到 EOF,则文件解析完成,退出解析程序。
1.5 Lex: The tool to generate DFA C code from R.E.
本节以 Flexc++ 的使用方法为例讨论 Lex 如何从正则表达式生成实现 DFA 的 C++ 代码;当然,Flex 生成 C 代码道理是一样的。
Flexc++ 将输入的词法规则(正则式和 token type 的映射)文件称为 rule file;Flexc++ 在处理 rule file 后,会生成一系列文件:
a class header file (
Scanner.h);internal header file (
Scanner.ih);a base class header file (
Scannerbase.h);lex.cc(词法分析器实现文件);
其中 lex.cc 不应该被修改,因为每次运行 Flexc++ 是都会被覆盖,而其他的文件只会生成一次,可以通过使用、添加 Scanner 类型的成员来达到一些特殊效果(这也是 Flexc++ 和 Flex 不同点之一);
1.5.1 Format of the Input File: *.lex
一般 Flexc++ 会将 rule file 看作两个部分,使用 %% 来间隔:
xxxxxxxxxxdefinitions // contains option specifications and definitions%%rules // contains the regular expressions (and their (optional) actions)
上半部分包含一些选项 / 规约,以及预先的定义,下半部分则包含正则表达式及其定义的行为;
Definitions Section
这一部分包含了:
命名的正则表达式(named regular expressions),方便正则式的复用,格式如下:
xxxxxxxxxxname pattern // 二者以空格隔开,正则式以该行的最后一个非空白字符为结尾// 这种命名的正则式不允许内部使用 comment(注释)// 其中 name 内部允许使用 '-'(hyphens)
Directives(控制指令):Flexc++ 提供了 命令行 options 和 directives 这两种方法来控制 Flexc++ 的行为。这里详细介绍 directives:
x%baseclass-header = "filename" // 定义生成的 ScannerBaseClass 头文件名。注意在 *.lex 中不接受目录分隔符(即 '/')%case-insensitive // 定义在 Flexc++ 匹配正则式时忽略大小写(匹配时全部转成小写,但是 token value 仍然保持原来的样子)%class-header = "filename" // 定义生成的 ScannerClass 头文件名%class-name = "MyScanner" // 定义生成的词法解释器的类名%debug // 让生成的词法分析器在运行时打印详细信息,但在生成代码时不会使用 #ifdef DEBUG%filenames = "basename" // 定义生成所有头文件的 prefix 名称%input-implementation = "sourcefile" // 指定用户自行实现的 Input 类的实现文件,自定义的方法在后面讨论%input-interface = "interface" // 指定用户自行实现的 Input 类的接口(头文件)%interactive // 指定生成的 Scanner 是否直接从命令行读取信息(std::cin)%lex-function-name = "funname"%lex-source = "filename" // 定义 lex.cc 文件名%namespace = "identifer" // 将生成的 Scanner 类置于指定 namespace 中,默认不使用命名空间%s namelist // 指定 start condition 的 ID,包括自身,使用空格隔开(什么是 start conditions?后面讨论)%x namelist // 指定 start condition 的 ID,不包括自身,使用空格隔开%skeleton-directory = "pathname" // 指定 Flexc++ 查找模板文件的目录%target-directory = "pathname" // 指定 Flexc++ 的输出目录
Rules Section
本部分仅包含正则表达式和行为的映射:
xxxxxxxxxxpattern action
action 可选(如果空的话,这条规则会被匹配并且不报错,但不作任何动作),并且和正则式使用 tab / 空格隔开;
action 中包含单行 C++ statement,或者一个占多行的 compound statement;
一个 action 可以是一个
|(vertical bar),表示和下一条规则使用同样的 action;
Comment in Rules File
*.lex rule file 的注释和 C++ 一样,/* */ 和 // 都行,缩进是无所谓的;有几点需要注意:
在 action 内的注释会被原封不动地生成到词法分析器中;
不能在 definitions section 的 named regular expression 中使用注释;
其他部分的注释不会保留到生成的词法分析器中;
Regular Expressions (Pattern) in Rules File
这里仅介绍和 Python/Perl/JavaScript 等常见应用中的正则表达式不同之处。
Flexc++ 不支持的:
分组、回溯引用;
Flexc++ 的需要注意的:
在字符集中,
-、\、]、^仍然具有特殊含义,其他原本有特殊含义的字符全部失去特殊含义(除非有\的作用);
Flexc++ 的不同之处:
.不包括换行;加上双引号后,pattern 会变成 literal string,例如
"[xyz]\"foo"表示字符串本身,而[xyz]"foo则是能匹配x"foo的 pattern;因为双引号有特殊含义,所以想匹配 literal string 的
"时,需要\"手动转义,或者使用 R 前缀;R 前缀:类似 Python 的
r"",表示 “转义字符串”,例如R"[xyz]\"foo"还是 literal string,不过包含中间的 backslash,等价于"[xyz]\\\"foo";十六进制数 和 八进制数:
\x2a(0x2a,十进制 42)、\123(0o123,十进制 83);使用命名的正则表达式:
{name};正向先行断言(Lookahead Assertion):
r/s,等价于常见的r(?=s);匹配 End Of File:
<<EOF>>;预定义字符集:Rules File 支持
[:predef:]的方式定义字符集内容。而不是用\w、\d、\s这样的方式;具体对应关系如下:注意:作为整体使用时记得还要包裹一层
[],主要是为了拼接方便;[:alpha:],表示所有字母,[[:alpha:]]等价于[a-zA-Z];[:digit:],表示所有数字(更多的不解释,同上);[:alnum:],使用[[:alnum:]]等价于[[:alpha:][:digit:]],也等价于[[:alpha:][0-9]],还等价于[a-zA-Z0-9],等价于常见的\w;现在知道为什么还要包裹一层
[]了吧?更多的:
xxxxxxxxxx[:alnum:] [:alpha:] [:blank:][:cntrl:] [:digit:] [:graph:][:lower:] [:print:] [:punct:][:space:] [:upper:] [:xdigit:]
反选预定义字符集:和常见语言中的正则引擎不同(将
\w换成大写的\W来反选),Flexc++ 直接用[:^alnum:]这种语法来反选;字符集的并集、差集:
[a-z]{+}[0-9]等价于[a-z0-9],[[:alnum:]]{-}[0-9]等价于[[:alpha:]];一个 pattern 最多只能有一个 trailing context(也就是说
/断言和$文末标记只能同时有一个);Start Condition: Flex/Flexc++ 和普通语言的正则引擎最大的不同就在这里!
<s>r:表示在 Start Condition ID 为s的子语言中,匹配r;<*>r:匹配所有 Start Condition 下的r;<s1,s2,s3>r:不多解释;<sc-list><<EOF>>:在 指定的 Start Condition 的子语言下的EOF;<sc-list> {compound rules}:在指定的 Start Condition 的子语言下才会生效的 rules,这也是为什么说 “start condition 用来定义子语言”;
详细信息参见 start conditions 一节;
Actions in Rules File
action 中可以使用 C++ 代码,并且调用预先约定的 member functions(详细请参见后文)来告诉 Flexc++ 生成的词法分析器会对这个 pattern 做何处理;
Start Conditions (Mini Scanners)
Start Conditions 可以用来定义子语言,最常用的用法是:识别字符串 / 注释(textural patterns),也就是告诉 Flexc++ 要生成的词法分析器应该如何描述字符串、如何描述注释、如何描述输入结构,等等。
我们之前在 definitions section 中提到两个指令 %s 和 %x 就是用来声明一个 start condition;
而在 rules section 中使用的 <id> pattern 则定义了词法分析器在子语言中的 actions;
当 actions 中调用 begin(StartCondtion_::?)(是 member functions 中的一种,参见)进入到一种子语言中的时候,不在这个子语言 start condition 定义(就是 <id> {compound rules})之内的规则全部失效,在 start condition 内的规则才会生效。
反之,调用 begin(StartCondtion_::INITIAL) 就是退出当前子语言,回到原本的环境,该 start condition 内的规则又重新失效,外部的生效。
我们发现这就像嵌套了两套规则系统,互相切换,这就是为什么说 “start condition 用来定义子语言”;
举个例子:
xxxxxxxxxx%x string // 定义 start condition ID 为 ‘string’,不包括自身// ... 其他定义 ...%%// ... 其他定义 ...// 这里识别 " 双引号\" { // action 是 compound statement// 具体作用在 member functions 中讨论more();// 表示进入 Start Condition 定义的子语言中begin(StartCondition_::string);}// 这里定义了 ID 为 ‘string’ 的 start condition 的处理方法<string>{// 表示如果再次遇到 " 符号,则退出当前子语言,回到原始的语言环境中(INITIAL)// 并返回 Token type,其中 token value 会被 matched() 返回// 更多信息参见 member functions 一节\" {begin(StartCondition_::INITIAL);return Token::STRING;}\\.|. more();}// ... 其他定义 ...
除了用前面提到的 <id> {compound rules} 定义规则,还可以用 <id>pattern(也是前面提到的)来完成,读者可以自行动手试一试。
进阶:(建议看完 Member Functions 一节后,再来回顾)
假设我想在子语言中嵌套另一种子语言,或者想要实现嵌套注释,应该怎么办?
我们可以修改生成的 Scanner 头文件,添加成员
std::stack<StartCondition_> d_scStack,让这个子语言的 start condition 能放到栈中,再定义方法:xxxxxxxxxx// 和已有的 begin() 访问权限一样,都放在 private 中private:void Scanner::push(StartCondition_ next) {d_scStack.push(startCondition()); // push the current SC.begin(next); // switch to the next}void Scanner::popStartCondition() {begin(d_scStack.top());d_scStack.pop();}这样我们在 actions 中就能用
push和popStartCondition了!
Member Functions in Flexc++'s Output Class Scanner
到目前为止,Flexc++ 生成词法分析器的运作原理就清楚了。通过 CLI options & Directives 控制 Flexc++ 生成物的名称以及其他定义,再给定 “pattern-action” 对,让生成应对 pattern 的 DFA 后将 action 直接复制到模板 Scanner 类的实现文件中,最终得到实现完整的词法编译器源文件。
本节就来看看 “模板 Scanner 类” 中已有的成员,哪些可以在 action 中使用,来实现词法分析器。
首先看 Scanner 类的核心方法 lex_(),它是进行词法解析的 main routine,也是各个 action 装载的位置:
xxxxxxxxxxint Scanner::lex_(){ // ... preCode(); // 这是空函数体,inline 在 Scanner.h 中,可以由用户自行定义行为
while (true) { size_t ch = get_(); // 获取下个字符 // ... // 执行 DFA 状态变换 switch (actionType_(range)) // 根据状态(对应的 pattern)选择 action { // ... maybe return // 这里面复制了 rules file 中定义的 actions } // ... no return, continue scanning preCode(); // 我们发现,空函数 preCode 的作用是让用户在每轮 action 没有返回 token type 时自定义行为 }}而我们能在 action 中使用的,就是类 Scanner 的如下成员函数:
注:为了方便理解,笔者调整了介绍的顺序,最好从上向下阅读,不建议跳着读。
在最后笔者会补充总结一下实现细节,帮助读者理解。
xxxxxxxxxx/** * 之前就提过的,用于切换 Start Condition 指定的子语言的函数。 * 不难发现 Flexc++ 会利用你在 definitions section 中定义的 start condition id * 生成一个 StartCondition_ 枚举类型,这样我们在 action 中就能使用了; */void begin(StartCondition_ startCondition);/** * 获取当前的 start condition(也就是处于哪个子语言中,还是原始环境中) */StartCondition_ startCondition() const;
/** * 仅当 directives section 中设置了 %debug 时,永远返回 true,否则永远返回 false * 这就是不使用 #ifdef DEBUG 宏的 Flexc++ 的替代做法 * 还可以由 setDebug(bool) 运行时设置(下面就不再介绍这个函数了)。 */bool debug() const;
/** * 将当前已匹配的文本(可以被 matched() 返回) * 插入到 Scanner 类的 output stream 中。 */void echo() const;
/** * 返回当前被 Flexc++ 处理的 rule file 文件名。 * 可以由 setFilename(string) 设置返回信息(不会重命名原文件)(下面也不再介绍这个函数)。 */std::string const &filename() const;
/** * 返回当前被匹配的文本的长度。 */size_t length() const;
/** * 返回当前正在解析行的行号。 * 注:如果在 directives 中定义 %lineno,则还会生成功能相同的 lineno() 方法。 */size_t lineNr() const;
/** * 返回当前已匹配的文本 * 这里能看出,Scanner 的模板实现中,对于已匹配的文本有单独的 text buffer 来维护。 * 可以由 setMatched(string) 来设置当前已匹配的文本(下面不再介绍这个函数)。 * * 重要提示:setMatched 可能很有用,例如在解析字符串时,源代码中的 "hello\n", * 可能需要词法分析器在解析后、返回这个 token 前,将两个字符 \n 转换成一个真正的换行符。 */std::string const &matched() const;
/** * 表示接受当前正在匹配的字符,并且已匹配的文本将作为下一个接受的文本的前缀。 * 相当于向已匹配文本的 text buffer 中 append 当前匹配的字符。 * * 注意:这在告诉我们,Scanner 对于已匹配的 text buffer,如果匹配到的 action 中什么都不做, * 则会清空 text buffer,只有使用 more() 才能向已匹配的内容追加。 */void more();
/** * Scanner 类的 output stream 的引用。 */std::ostream &out();
/** * 关闭当前的处理的 input stream,并从 stream 栈中弹出一个 input stream 作为当前的处理对象。 * 这就是 Flexc++ 可以同时处理多个输入文件/流的功能。与 pushStream 相对。 * * @return 当 stream 栈中没有任何 input stream 时弹出失败,返回 false,反之返回 true; */bool popStream();/** * 与上面操作相对。会将当前 input stream 压栈,并指定输入流/文件作为当前 input stream */void pushStream(std::istream &curStream); // interactive 词法分析器无法使用void pushStream(std::string const &curName);/* 除了 pop 和 push,还有 switch(不是栈操作),用的不多,不再介绍。 */
/** * 在上文已经介绍过了,让用户在每轮 action 没有返回 token type 时自定义行为 * 注意修改 Scanner.h 而不是修改 lex.cc */void preCode();/** * 和 preCode 一样是个空函数,可以在 Scanner.h 中由用户自定义 inline 实现。 * 这个函数会在一个 rule 刚刚被匹配并处理结束前被 lex_() 调用,传入的是当前匹配的 rule 的属性: * - PostEnum_::END: 一般是匹配了 input EOF,在 postCode 结束后 lex_ 会立即返回 0(EOF); * - PostEnum_::POP: 一般是匹配了 input EOF,但是 stream 栈里还有其他的 input stream,所以 lex_ 不会立即返回,而是继续处理其他 stream; * - PostEnum_::RETURN: 一般是匹配的 action 中含有 return(DFA 终态),会返回下个 token type,lex_ 在结束后会返回这个 type; * - PostEnum_::WIP: 一般是匹配的 action 中没有 return,会继续循环处理(不是 DFA 终态); * * 仍然不清楚流程的话建议回顾前文的 lex_() 的基本结构。 */void postCode(PostEnum_ type);
/** * 将字符 ch / 字符串 txt 重新放回 input stream 中(相当于压入栈顶,下一次就会读到)。 * 注意字符串 txt 压回会保证读取顺序(比如 txt 是 "hello",那么会从 o 向 h 依次压栈,确保读出的还是 hello)。 */void push(size_t ch);void push(std::string const &txt);
/** * 在当前已匹配的文本中,只接受前 nChars 个字符作为 token value(保留在已匹配的 text buffer 中等待 return 时传递出去) * 其余的退回 input stream(相当于 push),等待下一轮解析。 * * 用前面执行 DFA 的说法就是: * 将 input position at the last final 向前移动 nChars * 并且将 current input position 定位到相同位置(接受 token 时的规则)。 */void accept(size_t nChars = 0);
/** * 和 accept 作用类似,不过是 “只接受后 nChars 个字符作为 token value” */void redo(size_t nChars = 0);通过这些方法,我们反过来进一步了解了 Flexc++ 生成的 Scanner 解析词法的实现细节。下面补充总结一下:
Scanner 中有个临时存放已匹配文本的 text buffer;
在每轮匹配(解析)前,执行
preCode()、更新当前的状态(例如 current input position / input position at the last final);使用 pattern (DFA)匹配后,会现将刚刚匹配到的 string 设置到 text buffer 中(如果上次调用了
more()就追加),并且进入对应的 action 中;因此我们可以在 action 中:
使用
matched()查看当前匹配到的文本;使用
length()查看当前匹配到的文本长度;使用
more()请求 Scanner 不要清空这一轮的 text buffer,让下一轮识别的内容直接追加上去;使用
accept(n) / redo(n)来截取想要的文本、并把其余部分放回去;使用
push(str)直接向 input stream 放入指定下次要读的文本;使用
begin(SC)在下一轮解析开始时激活指定语言规则、冻结当前语言规则;使用
startCondition()获取当前子语言环境;使用
lineNr()获取当前解析的内容在源文件的行数;……
如果 action 会 return Token Type,那么 Scanner 会调用
postCode(PostEnum_::RETURN),并且作为 DFA 终态,输出 token;如果 action 没有 return,则 Scanner 会按情况调用
postCode(PostEnum_::END/POP/WIP),继续循环(不认为是终态)/ EOF 主动返回 0;只要没有调用
more(),那么 Scanner 会在下一轮解析前清空上一轮已匹配文本的 text buffer。有模板源码为证: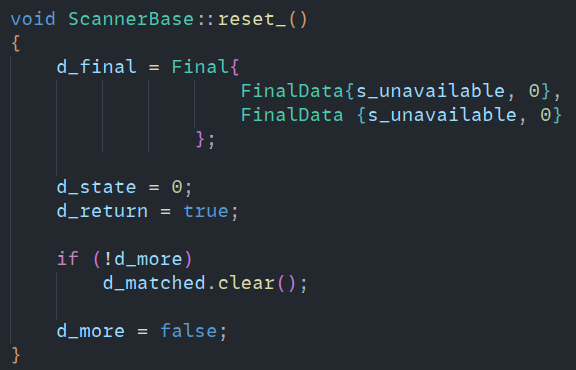
1.6 Lexical in Tiger Language
关注几点:
How you handle comments;
How you handle strings;
Error handling;
End-of-file handling;
Other interesting features of your lexer;
Tiger 语言的词法分析器需要识别:
保留字(RESERVED):
用于循环/分支:do, while, if, then, else, for, of, in, to, end, break;
用于定义/赋值:let, var, type, array, function, nil;
符号:
, : ; ( ) [ ] { } . + - * / = <> < <= > >= & | :=标识符(IDENTIFIER):A sequence of letters, digits, and underscores;Starting with a letter;
符合条件的注释:
May appear between any two tokens;
Start with
/*and end with*/;May be nested;
detect unclosed comments (at end of file);
整型常量 integer literal(NUMBER):词法分析阶段不考虑负数;
字符串常量 string literal:在
""(quotes)之间的零个或多个 printable character(包括空白字符)的序列,以及 escape character。解析字符串常量需要能识别 unclosed quote。其中 escape character 包含以下情况:\n,\t:linefeed, tab;\ddd:ddd is a 3-decimal number (not octal);\",\\;\f___f\:this sequence is ignored, wheref___fstands for sequence of one or more formatted characters including at least space, tab, or newline, form feed;\^c:^@(0, null, NUL,\0), mark the end of a string(在 Tiger 中支持\0在字符串中,不作为字符串结尾);^G(7, bell, BEL,\a), emit a warning of some kind;^H(8, backspace, BS,\b), may overprint the previous character;^I(9, horizontal tab, HT,\t), moves the printing position right to the next tab stop;^J(10, line feed, LF,\n), moves the print head down one line;^K(11, vertical tab, VT,\v), vertical tabulation;^L(12, form feed, FF,\f), to cause a printer to eject paper to the top of the next page, or a video terminal to clear the screen;^M(13, carriage return, CR,\r), moves the printing position to the start of the line, allowing overprinting;^Z(26, Control-Z, SUB,EOF). Acts as an end-of-file for the Windows text-mode file i/o;^[(27, escape, ESC,\e(GCC only)). Introduces an escape sequence;
Chapter 2. Grammar Analysis
目标:
识别从词法分析器传入的 token sequence 是否合法;
将识别合法的 token sequence 转为 parse tree(语法分析树)输出给 compiler 的下一环节;
为什么选择 parse tree 作为语法分析阶段输出的数据结构?
因为要生成一种方便机器识别的、方便后续解析工作的数据结构。人们恰好发现这种结构能很好地描述语法结构并且容易处理,主要基于以下观察:
程序的语言是递归定义的(需要有层次结构 Hierarchy);
Context-Free Grammar 能描述程序语法的组成(下面介绍);
因此 parse tree 这种树形数据结构可以用来表示程序的内部结构。
2.1 Background
事实上,如果只有正则表达式和词法分析,我们是无法解析复杂的程序语句和表达式的。
考虑这个表达式:
digits = [0-9]+;sum = (digits"+")*digits;
如果是这个表达式呢?
digits = [0-9]+;sum = expr"+"expr;expr = "("sum")" | digits;
问题是,这没法使用状态数小于 3 的自动机解析的。如果这样的嵌套更多,有 N 层呢?那么自动机的状态不能少于 N 个状态。
因为状态数为 N 的自动机没法记忆嵌套深度大于 N 的括号。这就是正则语言的局限性。
因此,像这样的 sum 和 expr,就不能仅仅用词法分析来解决。它们的规则就没法用正则表达式描述清楚;
所以我们需要在词法的 token 基础上,利用一种递归表示的方法来描述这种规则。
人们于是创造出一种简单的新的表示方法:上下文无关文法(Context-Free Grammar,CFG);
CFG 的表示方法就是 Context-Free Language,它和正则表达式一样,也是一种形式语言;
2.2 Context-Free Grammar
2.2.1 Production
我们之前提到过,一种语言(language)是字符串(string)组成的集合。而字符串是 符号(symbol)的有限序列。而符号则来源于这个语言所定义的有限字母表(alphabet);
对于语法分析而言,“string” 就是源代码,“symbol” 就是 lexical tokens(词法分析器的输出),“alphabet” 就是词法分析器输出的全部 token type 的集合;
一段上下文无关文法相当于一条语法规则,它是一组产生式(production)的集合。其中 production 的书写方式如下:
一个 production 满足以下规则:
其右侧包含 0 或者多个符号,每个符号要么是终结符(terminal,就是该语言中的 alphabet 中的一个 token,例如
INDENTIFIER),要么是非终结符(nonterminal);token value 被称为这个 terminal 的语义值(semantic value);
左侧是被定义的符号(又称非终结符),不能是一个 token。其中有种 nonterminal 比较特殊,被称为开始符号(start symbol);
另外我们规定,未明确给出一个 CFG 的 start symbol 时,其第一个 production 左侧的非终结符为 start symbol;
我们规定严谨的 production 的形式:
定义终结符
设
所以一个 CFG 所能代表的语言就可以用一个集合表示:
比如我们用 CFG 定义某种语言的语法:

其中 terminal 有:;、id、:=、print、(、)、num、+、,,
nonterminal 有 S(start symbol)、E、L;
Sidebar: 定义语言 CFG production 的技巧;
要定义一个左右括号匹配的语言:
;
2.2.2 Derivation
如果要分析一段代码中的语句是不是这个语言的语法、如何解析这个语句为语法树的结构,我们就需要借助 CFG 进行 “推导”(Derivation)。推导的执行过程如下:
从 CFG 的开始符号(特殊 nonterminal)出发,按照某条上下文无关文法展开每一个 nonterminal;
每步的展开,既可以展开当前 CFG 中最左边的 nonterminal,也可以展开最右边的,目标是向那段指定的代码推导;
重复展开的步骤,直至式中再无 nonterminal。如果能匹配,则该代码符合语法规范,并且语法解析成功,反之失败;
其中,上面每步展开 CFG 最左边 nonterminal 的做法称为 “最左推导”(leftmost derivation),每步展开最右边 nonterminal 的做法称为 “最右推导”(rightmost derivation);
当然如果每步展开的 nonterminal 位置不固定,那么既不是最左也不是最右推导,这种推导没有那么特殊。
另外还可以发现,一个 CFG 的推导的数量是无限多的,最终推导到同一个代码语句的方式也不唯一。
2.2.3 Parse Tree, Ambiguous Grammar, EOF
这里有几个零散的概念。
在语法分析器读入 terminals 时,也会读入 EOF(文件结束符,由词法分析器给定)。我们在 CFG 的书面表达中一般用 $ 来表示文件结束。所以,为了让 CFG 更完整,描述 EOF 只会出现在完整的 S-phase(S 为开始符号)之后,我们可以在 CFG 前添加一条规则 S' -> S$;
再讨论另一个概念。我们根据 derivation 的过程,将其中各个符号连接到从它推导出的符号(即:父符号做父结点,子符号做子结点),最终会形成一棵树形结构。这就是语法分析树(Parse Tree);两种推导过程可以拥有同样的 Parse Tree。Parse Tree 具有以下特点:
所有 nonterminals 都是中间结点、所有 terminals 都是叶结点;
Parse Tree 的中序遍历就是词法分析器的原输出(input of parser);
Parse Tree 包含了各操作符间的关系、优先级等信息;
一个无二义性的(Ambiguous)语句通过 CFG 推导后,一定能得到相同的 Parse Tree;
上面最后一条特点就是二义性的等价定义。当一种文法(CFG)在推导同一个语句时,能推出不同的 Parse Tree,则说明这个文法有二义性(Ambiguous Grammar)。比如我们之前看的文法 3-1:

用它来推导 id := id + id + id 能得到两个不同的 Parse Tree:
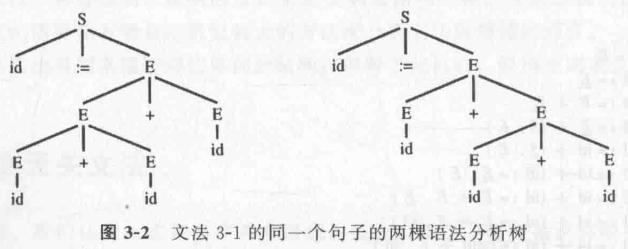
类似地,这种文法直觉上是没问题的,但也有二义性(解析 1 + 2 * 3):
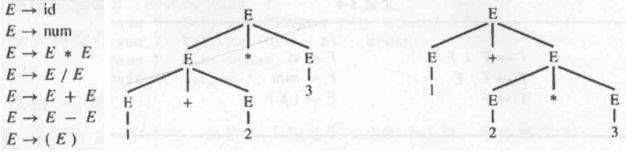
而二义性文法会给后续的语法分析带来困难,主要是因为我们(作为编译器一方)无法准确理解代码的准确含义,进而没法翻译成准确的汇编代码。
2.2.4 Disambiguation
如何去除这些二义性?
第一种方法是重构 CFG,因为大部分二义性文法都能转换为非二义性的。例如上面的文法可以通过修改 CFG 来体现各个运算间的优先级来去除二义性:
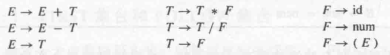
修改后的 CFG 添加了两种 nonterminal:
这样在无形中定义了乘法和加法的运算优先级、结合性,例如 T -> T * F 规定了 * 是左结合的。如果希望 * 右结合,就改为 T -> F * T;
现在这种语法就能消除二义性,让每条语句只能被 CFG 推导为唯一的 Parse Tree;
注:存在一些语言只有二义性文法,且无法转换。这种语言不能作为程序设计语言。
练习:以下的 CFG 表示的语言是否有二义性?如果有能否举个例子?应该如何修复二义性?
这么定义显然是有二义性的。例如
if E1 then if E2 then E3 else E4,可以解析为两种 Parse Tree:
if [E1] then [if E2 then E3 else E4];
if [E1] then [if E2 then E3] else E4;注意到这个问题是由于
else的结合规则规定不清导致的。我们需要修改 CFG,使其能够指明else需要和前方最近的then结合。于是我们需要区分then的匹配情况。定义:
MIF(match if)表示 then 和 else 是齐全的;
UIF(unmatch if)表示 if 后仅有 then;于是 CFG 改为:
或者更清晰地:
这种方法相当不直观,而且没有自动化的工具帮助我们,只能靠直接思考来解决;
第二种方法是添加约束/声明。我们使用原来的 CFG 有一个好处是可读性好。在这个基础上,我们要把一些事说清楚就可以加上一些约束/声明,例如上面提到的 “else 需要和前方最近的 then 匹配”、“加法、乘法都是左结合的,并且乘法优先级更高”,等等。
这种方法就能支持一些自动化工具了。例如 bison(一种处理 CFG 的语法分析器)就支持利用添加声明来消除二义性。
以 bison 为例,其内置了常见的用于规定二元操作符的语法:
%left +:表示+符号是左结合的;先定义
%left +再定义%left *:表示+、*都是左结合的,但+优先级高于*;
2.3 Top-down Parsing
现在我们正式讨论如何根据语言的 CFG 来解析一个语句是否为该语言的语句。
本节主要讨论一类 “自上而下” 构造 Parse Tree(将 nonterminal 替换 terminal,比较直观)的语法分析算法,称为 Top-Down Parsing;
2.3.1 Recursive Decent Parsing
Example
Top-down parsing 中,有一种比较简单直观的方法,称为 “递归下降”(Recursive Decent)算法。它的原理就是把一个 production 变成递归函数的一个子句,因此一些简单的文法使用它就能轻松解析。
我们先考虑简单的情况,假如一个只有右结合运算的 CFG(为什么必须只有右结合?因为目前还处理不了左结合):
然后 input tokens sequence 为:
第一步应该选哪个 production?答案是都可以,因为对递归下降算法而言,先选谁最终都能得到唯一正确的 Parse Tree(如果无二义性的话);
选择
再向下继续选择
选择
继续匹配发现
选择
继续匹配发现
这个选择整体失败,回溯到上一级;
选择
向下继续选择
……
选择
继续匹配
Left-Recursive Grammar
现在回过头讨论一下,我们之前说 “现在还处理不了左结合”,这是因为一旦遇到了形如
不过我们可以通过一些手段消除左递归:
形如
同理,更一般的情况
这样我们可以在递归下降之前消除一次左递归,就能正常使用了!
Conclusion
总而言之,递归下降方法的优点明显:方便理解、方便实现;
不过缺点也很显著:多层的递归、回溯,造成了比较大的性能问题;
2.3.2 Predictive Parsing
LL(k) Grammars
Recursive Decent Parsing 的缺点是执行较慢、递归层数较多。为了改进这个问题,人们引入了另一种方法,称为预测式分析(predictive paring);
预测式分析和递归下降很像,但是前者会预测现在应该使用什么 production 来解析当前的 sequence;
预测式分析的原理是通过向后多看几个 tokens 再做决定,规避了失败回溯的情况。
其中,预测式分析支持 LL(k) Grammars。所谓 LL(k):
第一个 L:从左到右扫描输入,left-to-right scan of input;
第二个 L:最左推导,leftmost-derivation;
k:向后看 k 个 token(s) 来做预测;
另外我们定义,能够采用 LL(k) 的预测式分析来正确解析的语言,被称为 LL(k) Language,其 CFG 称为 LL(k) Grammar;
Example
本节我们以 LL(1) 为例介绍。现在来看最简单的 LL(1) Language 的例子:
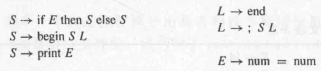
这个例子中,每个 production 前面都有唯一一种 terminal/non-terminal。这样 LL(1) 就不会出现错误。
回想 Mini-Basic 语法,它就是一种 LL(1) Language,因为它也是利用语句的第一个关键字来识别语句的种类,然后 expression 则采用的是逆波兰表达式转为后缀式来解析,不过这个例子中没有复杂的 operators,所以更简单。
对应的 LL(1) Parser 代码如下:
xxxxxxxxxxenum token { IF, THEN, ELSE, BEGIN, END, PRINT, SEMI, NUM, EQ };/* Input */extern enum token getToken(void);/* Custom Exception Handler */extern void error(void);
/* Current Token */enum Token tok;/* Get next token */void advance() {tok = getToken();}/* try to parse */void eat(enum Token t) { if (tok == t) advance(); else error(); }
// 为每个 non-terminal 定义一个互递归函数// 使用最开始用递归的方法来解析。如果出错就返回上一步void S(void) { switch (tok) { case IF: eat(IF); E(); eat(THEN); S(); eat(ELSE); S(); break; case BEGIN: eat(BEGIN); S(); L(); break; case PRINT: eat(PRINT); E(); break; default: error(); }}void L(void) { switch (tok) { case END: eat(END); break; case SEMI: eat(SEMI); S(); L(); break; default: error(); }}void E(void) { eat(NUM); eat(EQ); eat(NUM); }Left-Factored & LL(1) Languages
另外,我们能发现:LL(1) Language 中,对于一个任何 nonterminal(向后看一个 token),总有且仅有一个 production 能正确解析;
因此一个 LL(1) Language 的 CFG 可以由一个 2D Table 等价替代:
一个维度存放当前需要展开的 nonterminal;
另一个维度存放下一个 token 的情况;
一个 table entry 存放对应的 production;
这样 LL(1) Language 的语法分析器是可以通过给定 CFG 而自动化生成的!
现在回忆上一节最开始的例子,看看我们能不能用 predictive parsing 的方式解决它:
我们发现这个 CFG 用 LL(1) 是没法预测的,因为:
对 nonterminal
对 nonterminal
对此,我们类比 NFA 和 DFA 的区别,我们要将相同的部分进行提取,这称为 left-factored,上面的 CFG 可以转变为:
将共同的
将相同的
恭喜!现在它成功变成了 LL(1) Language!我们可以继续使用 predictive parsing 来解析它了。
所以和梯度下降算法类似,预测式分析前,必须要进行 left-factored 的提取过程。
LL(1) Parsing Process: Example
我们现在以上面的 LL(1) Grammar 为例:
| token\non-term | int | * | + | ( | ) | $ |
|---|---|---|---|---|---|---|
T | int y | (E) | ||||
E | T X | T X | ||||
X | + E | |||||
y | * T |
对于一个输入
| Stack | Input | Action |
|---|---|---|
E $ | int * int $ | T X(查表 |
T X $ | int * int $ | int y(查表 |
int y X $ | int * int $ | Got Terminal(pop) |
y X $ | * int $ | * T(查表 |
* T X $ | * int $ | Got Terminal(pop) |
T X $ | int $ | int y(查表 |
int y X $ | int $ | Got Terminal(pop) |
y X $ | $ | |
X $ | $ | |
$ | $ | Accept |
How to Construct a Predictive Parsing Table
考虑任意一个中间状态:
或者说:
更进一步地,我们应该如何找到 “
定义:
计算
对于所有(每个逐个) production:
添加
(含义解释:所有
重复上述步骤,直至
如果到最终一步还是存在
(含义解释:最终
其中:
这个时候只能使用
同样,我们需要找
定义:
计算
对所有(每个逐个)
如果
添加
(含义解释:所有在
重复上述步骤,直至
如果到最终一步还是存在
(含义翻译:如果
因此,借助
对 CFG 中的每一条 production
对每个非空 terminal
注意不是
解释:如果
这里讨论了所有
如果
解释:如果
这里讨论了所有
如果
解释:如果
这里讨论了所有
上面的 3 条规则将 LL(1) production 的信息彻底转换为一个 2D Table 以供解析。
Caution
注意:如果在转换途中发现一个 table entry 被第二次填写,则可能是以下问题:
此语言的 CFG 具有二义性;
此语言的 CFG 没有消除 left-recursion;
此语言的 CFG 没有 left-factored;
Error Handling
我们希望 Parser 在遇到错误后停下来,因此:
Insert Token:在出错的地方根据 production 假装有个合法的 token 在那(相当于补了一个 token),并报错。但可能有 endless loop 的风险(如果补充的 token 还是错误了);
Delete Token:在出错的地方跳至下一个合理的 token 处,也就是
Summary
虽然对于 LL(1) Language,上述的 parser 实现方案已经相当齐全了,但是值得注意的是,目前大多数实用的高级语言都不是 LL(1),因此只了解 LL(1) Parsing (也就是 Top-Down Predictive Parsing)是不够的。我们需要更强力的解析策略。
2.4 Bottom-up Parsing
“自下而上”地构造 Parse Tree 实际上应用比 top-down parsing 更普遍。
人们是在基于 top-down parsing 的基础上讨论出了这种方法,效率可观、并且在实际应用中更为普遍。
由于这个方法的特性,人们也将这种 parsing method 称为 “LR Parsing”:
L 表示从左向右阅读/解析 token;
R 表示使用 最右推导(Rightmost Derivation);
最后 LR Parsing 的特性是:
能支持左递归、也不需要 left-factored;
LR Parsing 的核心思路是:
将一个输入的 token 串(string),尝试使用 production
重复识别、替换的步骤,直到 string 成为一个 start symbol;
Important
反过来看,LR Parser 使用的是最右推导!
这样,在推导序列中,
这个特性会被用到接下来的解析实现中。
2.4.1 Shift-Reduce Parsing
如何实现 LR Parsing 中 “将 string 中的
我们需要一个实现思路:将 token string 看成两个 substring;
右边的 substring(
左边的 substring(
注:为了方便分析的时候查看二者的分界情况,我们后面会用 “
” 来表示分界(实际在 token string 中不存在);
在实现前,我们定义两个动作:
Shift:将
Reduce:在
举个例子,LR Parsing 过程如下:
我们要识别 int + (int) + (int) $,那么:
第一步:
第二步:
第三步:
第四步:
……
现在我们考虑如何在代码层面实现它。
左边的 substring 可以放在栈数据结构中;
shift 操作是将一个 terminal 推入栈中;
reduce 操作是从栈中弹出 0 或多个 symbols(可能有 terminal,也可能有 non-terminal),根据 production 合成一个 non-terminal 后再推入栈中;
有点像表达式运算的过程;
2.4.2 LR(k) Parsing & DFA
好现在有个问题:怎么能准确地知道什么时候 shift、什么时候 reduce,才能保证最终转换成 start symbol / 抛出解析错误?
例如为什么 parser 知道在第二步的时候,不是继续 shift,而是先执行 reduce?
好办!我们借鉴 Top-Down Parsing 中的 predictive parsing 的思想,可以通过左边 substring(放在栈中)的已有的情况来判断应该使用什么 production。这个根据栈中状态决定行为的方法,还可以用 DFA 进行包装!也就是说:
DFA 输入是当前 stack 中的内容,并且维护一个当前状态所在结点;
DFA 执行方案就是:
如果 stack 中的内容不足以使 DFA 发生一次状态转换,那么执行 shift;
如果 stack 中的内容对应 DFA 中的一条可行转换,则在检查转换条件(关于转换条件,不是查看 stack,而是查看当前的输入 symbol。参见下面的例子)后,如果满足,则执行 reduce;否则继续 shift;
每次 reduce 会重置 DFA 的状态为最初状态;
如果 DFA 每次查看 stack 上前 k 个元素,则成这种解析方式为 LR(k) 的,如果有一种 language 只需要 LR(1) 就能正确解析,则称这类 language 为 LR(1) Language,称这种 language 的 CFG 为 LR(1) Grammar;
仍然举之前经典的例子,这就是一个 LR(1) Language:
也就是说这个语言构建出的 DFA 每次只需要看栈顶的 1 个元素就能正确解析。它对应的 DFA 如下:
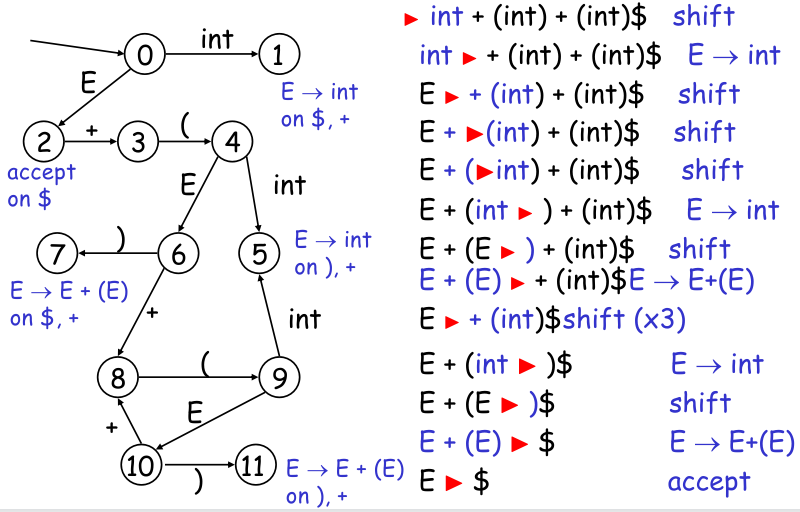
那么好,我们如何构建这个 DFA?答案还是 2D Table,但是有 2 份:
第一份是 transition 表,描述根据栈顶的信息接下来可以转到的状态:
一个维度存放当前的栈顶的 symbol(可能有 terminal/non-terminal,可以画条线区分)的可能性;
另一个维度存放 DFA 的当前状态的可能;
entry 存放 DFA 下一个状态结点;
第二份表是 action 表,描述在状态转换后可以进行的动作:
一个维度存放当前的输入 terminal(是输入,而不是栈顶,所以不包含 non-terminal) 的可能性;
另一个维度存放 DFA 转换后的状态的可能;
Table Entry 存放 parser 可以进行的动作(shift / 哪一类 reduce);
我们可以将这两张表合起来(放在一起,仅仅是行列的元素相似,但是含义不一样)。这样,我们将合并的表的 terminal 的列(既有 transition 又有 action)称为 action table,将 non-terminal 列(只有 transaction)称为 goto table;
2.4.3 LR Parsing Algorithm
我们回顾一下之前的做法就会发现,“每次 reduce 会重置 DFA 的状态为最初状态”,并不是一种高效的做法,因为我们会因此需要从栈底开始一个个重新进行 transaction。我们应该借助已经解析的部分,推断出 reduce 后 DFA 应该位于哪里,这样就能节省一定的状态转换步骤。
Q&A
例如对于 LR(1),我们只需要记录每次 1 个 symbol 和 state 的对应关系 <sym, state> 就行,方便下次 reduce 后查看到这个符号对应的状态。以上面的 int + (int) + (int) $ 解析为例:
先写入
<dummy, 0>的关系(表示当前栈空,对应状态 0);根据状态 0 + 输入
int,查询 action 表后得到 shift;根据状态 0 + 栈顶int(因为 shift 后栈顶一定是它),提前查询 transition 表得到下一个状态是 1;故转换至新状态 1,则记录<int, 1>,表示当前栈顶为int,对应状态 1;根据状态 1 + 输入
+,查询 action 表后得到 reduceE -> int。注意!这里栈里没有信息(<dummy, 0>),我们只能退回状态 0,将E入栈。由于我们知道 reduce 的结果一定是E在栈顶,因此可以在入栈前提前查询 transition 表(对 non-terminal 来说就是 goto table) “状态 0(查栈顶<dummy, 0>得知的将退回的状态) + 栈顶E”,转移结果是状态 2,所以记录<E, 2>后 reduce 入栈,并直接到状态 2;继续根据状态 2 + 输入
+,查询 action 表后得到 shift;根据状态 2 + 栈顶+得到下一状态 3(这里记录<+, 3>);故转换至新状态 3;根据状态 3 + 输入
(,查询 action 表后得到 shift;根据状态 3 + 栈顶(得到下一状态 4(记录<(, 4>);故转换至新状态 4;根据状态 4 + 输入
int,查询 action 表后得到 shift;根据状态 3 + 栈顶int得到下一状态 5(记录<int, 5>,注意和前面已被合并的<int, 1>是两回事了);转换至状态 5;根据状态 5 + 输入
),查询 action 表后得到 reduceE -> int,注意!这个时候,只需要退回到目前栈顶(存放的状态,即<(, 4>,就是状态 4 并将E入栈。再次地,由于我们知道 reduce 结果是E在栈顶,因此可以在入栈前查询 goto-table “状态 4 + 栈顶E”,转移结果是状态 6,因此记录<E, 6>后 reduce 入栈,并直接到状态 6;这个时候相当于
4就是栈中其他所有 symbol 的最终状态;……
2.4.4 Constructing LR Parser DFA
现在的问题还是,如何构建这个 LR(1) 的二维表/DFA?
我们先引入 LR(1) item 的概念:
当前输入的 terminal(look ahead terminal)需要是
为了描述方便,我们约定一个 trivial case:
当栈为空的时候,我们目标很明确,就是规约成
这样就能用 LR(1) item 来描述 DFA 状态了。我们举个例子:
假设某时刻 LR(1) parser 的状态用
(,则 shift;假设某时刻状态
+,则 reduce;
现在我们知道
还有,我们现在还没搞懂后面缀的一个 “+” 是怎么得出来的?别急,继续向下看。
例如假设某时刻的状态
哦!原来是用类似递归的方式来描述当前 parser 的状态,后面缀的部分其实是递归上一层的解析器的解析要求!
我们把上面的操作定义为 Closure Operation,我们认为,对一个 LR(1) item 的闭包操作如下:
xxxxxxxxxxprocedure Closure(items):# 这步骤称为闭包的原因就是它会不停地在集合中按照某种方式运算# 并加入结果,直至结果稳定
repeat util items is unchanged: for [X -> a.Yb, w] in items: # 对每个下一个是 non-terminal 的 item for each production Y -> r: # 用对应的 production 展开,并以 First(bw) 讨论情况加入后缀 for b in First(bw): items += [Y -> .r, b]现在,我们需要构建一个 LR Parser 的理论工具已经准备完全了。接下来我们完整地走一遍构建流程。
初始状态栈为空,状态
由于
经过两轮计算后,上述结果稳定,也就是上述 items 为
Closure({S -> . E $});可以将相同前缀合并同类项(例如:我们定义:
一个 items 闭包就是一个 DFA 的状态,因此上述 items 就是 DFA 的真正的状态 0(把一开始没求闭包的状态称为 partial state);
对一个闭包上的所有
其中
得到当前 DFA 状态 0 后,考虑 transition:将状态中的所有 items 的 dot 向后推进一位,根据推进的 symbol 绘制出一条出边;进而得到下一状态的 partial state;形式定义如下:
xxxxxxxxxxprocedure Transition(State, Y):# 不同的 Y 会指向不同的状态结点items = {}for [X -> a.Yb, w] in State:items += [X -> aY.b, w]return Closure(items) # 表示最后求闭包才能从 partial state 转变为真正的状态重复第二步的 “求闭包” 得到真正状态以及 reduce 标记、重复第三步 “绘制 出边”,(合起来就是
Transition)直至状态绘制完全。
下面是一个完整实例:
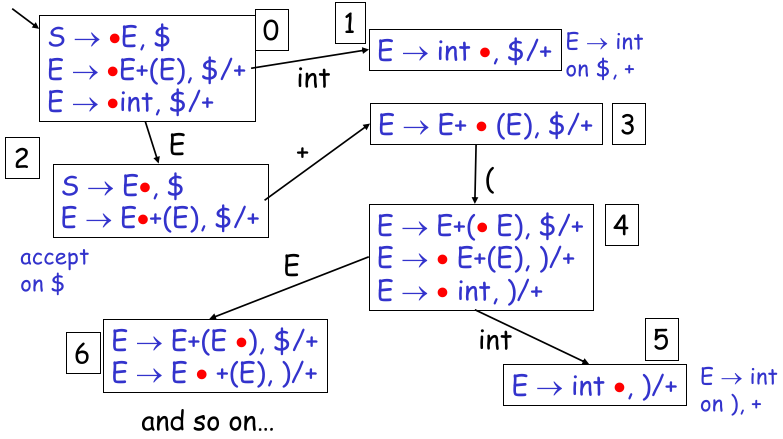
由 DFA,借助之前的知识,我们能够轻松地将其转换为二维表。
也就是说,上述一长串过程(从 CFG 到 LR Parsing Table),全部都可以自动化生成;
2.4.5 Problem I in LR Parsing Table: Shift/Reduce Conflicts
按照上述方法生成的二维表能直接用来作为 LR Parser 了吗?可惜还有点小问题。
考虑一种情况,如果一个 DFA 状态中同时含有
出现这种情况,原因大多是 CFG 存在二义性。
例如我们之前举过的例子:
它在生成 Parsing Table 时,就会有如下情况存在一个状态结点中:
我们可能需要对这种情况的默认行为,于是在某些工具(如 bison)中,默认行为就是 shift。
不过回想一下前面说,我们可以通过添加约束/声明来消除二义性,比如在下面的二义性文法中:
可能出现
我们在 bison 中添加结合性声明,以及基于先后的优先级声明(统称为 directives),来消除二义性:
xxxxxxxxxx%left +%left *
那这是怎么实现的?以 Bison 为例,它约定,如果出现 shift/reduce conflict,则:
检查所有 directives 中给定的优先级。input terminal 和 rule(指需要 reduce 的 rule)的优先级更高就遵从谁的。item 的优先级取决于其 production 右侧的最后一个 token(terminal);
如果优先级相同,则检查 directives 中的结合性,如果 input terminal 是右结合的,则执行 shift;左结合反之;
为什么 input terminal 右结合的话 shift?
考虑一个情况:
如果没有涉及优先级的 directives,则也执行默认行为(shift);
2.4.6 Problem II in LR Parsing Table: Reduce/Reduce Conflicts
shift/reduce conflicts 是解决了,但我们发现按照 shift/reduce conflict 的思路查找,还有一个问题。
考虑这种情况:
这种情况还是因为 CFG 的二义性。例如下面的 CFG:
注:
和上面的等价而且不会有问题 :(
一方面,比较遗憾的是 reduce/reduce conflicts 在理论上是没办法直接解决的(只能使用 default behavior);
但另一方面,reduce/reduce conflicts 通常是因为 CFG 写的已经相当不规范了,像上面的例子,我们可以通过简单的等价重构来避免这个问题。
2.4.7 Optimization: LALR(1)
总结一下,我们介绍的 LR Parser 通过 LR(1) item 构造 DFA 和 2D-Table,再利用优先级和结合性声明来消除 shift/reduce conflicts,最终达到解析语法的目的。
但是有个问题是,这样构造的效率还是太低了,像一个简单的语言,LR(1) Parser 就需要大约 1000 个状态结点来构造一个 DFA!所以实践中一般的 parser generator 不这么实现 parser;
我们注意到,LR(1) Parsing Table 虽然很大,但是 DFA 状态结点中的 item 有很多相似的,例如
因此,我们可以考虑把同一个状态中只有 lookahead terminal 不同的 items 合并起来:
所以我们定义,一组 LR(1) items 的核心(core)就是这组 items 去除 lookahead terminal 后的 production 的集合;
两个 LR(1) Parser 的 DFA 状态结点可以合并,就当且仅当这两个状态结点的 core 是相同的。我们称合并后的状态结点为 LALR(1) state(Look-Ahead LR(1) state);
将 LR(1) DFA 中所有状态都尽可能合并完(直到所有 state 的 core 都两两不再相同),最终得到 LALR(1) DFA;
虽然 LALR(1) 可以显著减少 DFA 状态,但是它也会引入 reduce/reduce conflicts 的问题。例如:
两个状态
但幸运的是,这样的情况几乎不会发生(除非人为构造一个奇怪的语言),也就是说只要是一个符合人类习惯的正常语言都不会出现这个问题,我们称这种语言为 LALR(1) Language,就像 admissible heuristic function 大多数情况下都有 consistent 性质一样。
于是,LALR(1) 就成为一种语言、parser generator 的事实标准。
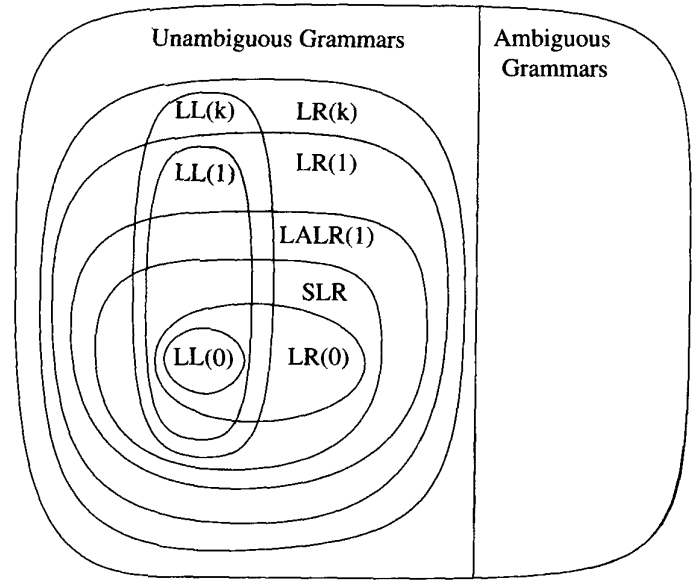
现在我们已经完全搞清楚了如何自动生成 parser 了。只要再加上 error handling 就能实现一个 parser generator 来帮助我们生成一个 LALR(1) Parser 了;
注:这个 parser 如何生成最终要输出的 parse tree,在已经了解算法的情况下就很好办了,只要在解析的中途从下到上利用 non-terminal 和 terminal 在 shift 以及 reduce 阶段顺便构建一个 parse tree 的数据结构就行。
2.4.8 LR(1) Error Handling
和 Top-Down Parser 一样,遇到错误后我们有两种方案:
Error Throwing:立即停止并报出错误(可能会因为连续的简单的错误反复重新编译);
Error Recovery:记录错误并报出,但尝试继续解析(可能因为一处错误导致报出一系列其他错误);
这两种方案都有点问题,不过实践中用第二种比较多。
在 Error Recovery 中又有 3 种调整方式:
delete tokens;
insert tokens(可能出现无穷循环问题);
substitute tokens;
以及两类使用方式:
local recovery:在错误发生的位置调整;
global recovery:在错误发生之前的位置调整;
Local Recovery & Delete Tokens
先讨论 local recovery - delete tokens 这种组合。
借鉴 Top-Down Parsing 的错误处理思路,在遇到错误 token 的时候 skip(也就是 delete)到下一个目标 token 处,这个目标 token 就是我们想要的 synchronizing token,就是让 parser 状态重新恢复到正常的必要步骤。
在 Top-Down 中使用的 synchronizing token 实际上是栈顶
我们应该加入如下 Error Recovering CFG:
这样出现错误时就能恢复了。举个例子,加上在上面的 CFG 前提下,遇到的输入以及栈的状态:
NUM PLUS ( NUM PLUS |> @#$ PLUS NUM ) PLUS NUM
下一步发现这个 token 是
NUM PLUS ( |> @#$ PLUS NUM ) PLUS NUM
这里 pop stack 相当于抛弃了那些 tokens;
到这里开始发现可以匹配
NUM PLUS ( @#$ PLUS NUM ) |> PLUS NUM
此时栈中的状态是:exp PLUS (error),规约为:exp PLUS exp,然后状态恢复正常,继续 parser,实现了 Error Recovering;
Global Recovery
global recovery 的策略常常使用一个被称为 “Burke-Fisher error repair” 的实现;
Burke-Fisher error repair 思想如下:
Tries every possible single-token insertion, deletion or replacement(尝试了所有 3 中调整方式)at every point in the input up to K tokens before the error is detected;
e.g. :
K = 20: parser gets stuck at token 500; all possible repairs between token 480-500 tried;best repair = longest successful parse;
其实现方法就是维护两个栈,第二个栈保留第一个普通栈 reduce 后的原始 token(方便出现问题后在 K 个 token 长的滑动窗口中查找问题),也就是第二个栈比第一个栈晚 K 步而已;

于是可能的尝试有 N + 2k * N 个:delete tokens(K)、insertions((K+1) * N)、replacement(K(N-1));
这样的开销在错误处理的情况下是可以接受的。
2.5 Yacc: The tool to generate parsing table from CFG
现在我们已经掌握了基本的语法分析的知识了,这节介绍实践中如何使用一个别人写好的 parser generator;
一个比较常用的 parser generator 就是 yacc,能够在你指定 CFG 和优先级、结合性声明后自动化生成一个 parser。
也就是说,Yacc 之于语法分析器,就像 Lex 之于词法分析器。
附注:
Lex、Flex、Yacc、Bison究竟有什么关系?
Lex和Flex都是词法分析器,但是Flex是在Lex基础上发展起来的(Flex is the successor of Lex);
不过它们的 rules file format 有所差别,前者允许自己的代码控制词法分析器,而后者更严格一点;
Yacc和Bison都是语法分析器,但是yacc更早出现,而Bison是 GNU 对Yacc的另一种替代的开源实现;
它们的 rules file format 也有差别;
总的来说,
Flex和Bison是 GNU 开源免费的,Lex和Yacc是 Unix SVRx licenses 下可以自定义商用的版本;我们一般学习建议使用
Flex&Bison组合;摘自 Bison and Yacc;
Chapter 3. Semantic Actions & Semantic Analysis
本章内容额外摘自:
3.1 Where we are now?
我们再次回顾一下 Compiler 设计的各个阶段(简化版):
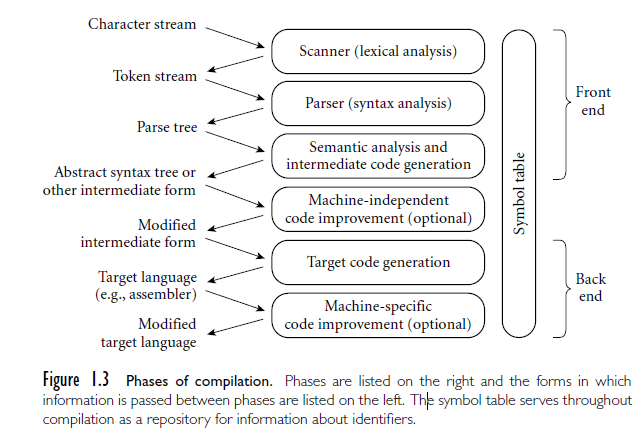
我们前两章已经完成了词法分析(lexical analysis)和语法分析(syntax analysis 或 grammar analysis),能够成功地抽象出程序的语法结构,并且以 parse tree 的形式给出语法分析的结果(即程序关于 Context-Free Grammar 的层次结构),证明了程序是符合 CFG 的约定的。
但是,只考虑 context-free 的东西是不行的,是没办法正确地编出一些程序的。
举个例子:int a = "I am a string";,这种语句它能正确地通过词法分析和语法分析,但实际上它是有问题的。那你说它究竟违反了哪一条 Context-Free Grammar?答案是并不违反。
所以,要定义一个高级语言,除了词法、上下文无关文法的约定以外,还需要另一种抽象的约定,用来限制上面的 “上下文相关”(Context-Sensitive)的信息。
这个 “上下文相关的约定”,人们将其称为 “Semantic Rules”,要解析这些约定,就要借助 compiler 的下一个阶段的工作:语义动作 & 语义分析(Semantic Actions & Semantic Analysis);
而 CFG 和 Semantic Rules 这两种约定合称为 “Syntax Directed Definitions”(简称 语法制导定义,将语法和语义结合起来定义)。只有将语法(grammar/syntax)和语义(semantic)结合起来,才能较为全面地描述一个语言。
思考:为什么既然在 semantic analysis 阶段,需要把语法和语义一起考虑,那为什么 compiler 设计的时候不直接一股脑全放到 parser 中,合并起来,让 parser 直接生成 Abstract Syntax Tree(能同时描述语法和语义的数据结构)不行吗?
因为,这样的设计是通过大量的实践得出的。如果把二者合成一个阶段,则耦合性上升、可配置性就下降了。
对于不同的语言的编译器,我可能需要写很多重复的模板代码(boilerplate code),这是人们不喜欢的,而且会增大错误几率和调试成本。
因此人们为了高度可定制化、代码重用性以及高度模块化,从更高的抽象层级上把 Syntax/Grammar 和 Semantic 拆开分析。
实际情况是,为了省事(因为还是需要把 CFG 和 Semantic Rules 放在一起的,如果物理上写成两个程序就不好实现了),人们把这两个阶段合起来(但思想上还是有两个阶段),使用一个工具来完成上述语法分析、语义分析的任务。这就是 Bison。我们在本章末尾介绍它的使用方法。
3.2 Semantic Rules, Attribute Grammar, Abstract Syntax Tree
那么所谓的 semantic rules 究竟怎么约定上下文相关的信息?
首先我们要知道 “上下文相关信息” 究竟是什么:
语义值(semantic value):就是这个 token 的“通俗意义上的”值,例如
int a = 1;这里假设有个 token type 是DIGIT,那么在 parse tree 中 1 所代表的结点 token type 是DIGIT;而它的语义值就是 1 本身;一般这个信息应该由 parser 存放在 semantic value stack 上,以供后续语义分析等环节使用。
non-terminal 也是有 semantic value 的,例如在一个交互式解释器 / 计算器中,一个表达式 expression 的语义值就是一个数字;在一个编译器中,一个表达式的语义通常是描述这个表达式结构的树结构;
作用域(scope)信息:典型需要结合上下文得知的信息。它可以体现在:
某些语言会定义一些作用域,不同的作用域下变量的使用情况?
如何发现某些变量在定义前被引用?
类型(type)信息:对于一个静态类型语言,编译器可以在语义分析的阶段拿到并分析 terminal 的具体类型,以此判断这种语义是否正确;
文章开头的类型错误的例子就需要这种信息来识别;
……
这些上下文信息构成的语义也被称为 “static semantics”,意为能在编译阶段(compile-time)就能得知的上下文信息。相对的是 “运行时上下文”,它的正确性只能由编程人员自行保证,编译器在整个编译阶段都不会管理。
总而言之,semantic rules 就是在描述这些上下文信息怎么从 parse tree 上被获得、怎么解析和计算。
那么相对地,我们需要严格的、形式化的方法来定义这些 “上下文相关信息”,这就是 attribute grammar:它描述为了明确语义,对于一个 symbol 我们需要哪些上下文信息、如何组织这些信息。
Attribute Grammars define what semantic information is needed and how it is structured, while Semantic Rules define how this information should be computed or derived during parsing and compilation.
In other words:
Attribute Grammars provide a framework that extends CFGs by associating attributes with grammar symbols and specifying rules for attribute computation;
Semantic Rules operate within this framework to dictate how those attributes are computed for each production rule in the grammar.
而为了形式化、准确地定义上下文相关信息,Attribute Grammar 本身就是一种形式语言,它和 正则表达式 一样,本身都是一种上下文无关文法,用来描述上下文有关的信息。
它的做法是,向 parse tree 中的 non-terminal 定义一些上下文相关信息的类型(这里被称为 “attributes”),然后利用 semantic rules 去在 parse tree 上解析、运算这些 attributes 的值(value)。semantic rules 可以定义一些 side effects(例如打印一些内容、更新一些 global variables 等),在运算过程中可以顺便执行。当我们利用 attribute grammar 和 semantic rules 充分解析了 parse tree,在 parser tree 的基础上,我们抛弃掉不必要的 non-terminal,在树上点缀上下文相关的信息,会构建出一棵能够描述代码“几乎”全部含义的抽象语法树(Abstract Syntax Tree,AST)(其实也是利用 semantic rules),这步就是 Semantic Action(语义动作);
注 1:现在还有些上下文相关信息,例如类型检查、作用域关系没有处理;
注 2:如果是这里编写的是直接运算出结果的计算器,或者解释型语言的交互型解释器(REPL),又或者是没有优化的解释器(Interpreter),那么 semantic action 阶段就可以直接执行指令了,这个时候有 side effects 就比较重要了;
注 3:有一部分学者,以及教授此课的臧老师,都将 semantic action 归于 syntax analysis(语法分析),并认为语法分析阶段产出 AST,其实也没有问题,只是设计上的微小差别。更何况实际情况就是 Bison 工具一起处理了语法分析和语义动作。
最终,还需要执行类型/作用域等等上下文信息的补充,并得到一些附加的信息(位于 Environment Table 中)。这一阶段(语义分析,Semantic Analysis)才算真正结束。
3.3 Synthesized Attributes & Inherited Attributes
Attribute Grammar 中将这些 attributes(即上下文相关信息)分为 2 类:Synthesized Attributes 和 Inherited Attributes。
Synthesized Attributes:在 semantic rules 中,总是通过 parse tree 中的子结点的 attributes 计算 / 解析而来的属性。也称 “S-Attributed Definitions”;
这种属性显然对于 Bottom-Up 的解析方法比较友好,也是最常用的 attributes,目前大多数解析 semantic rules 的方法都是通过它来完成。
这样的话,我们进行 semantic analysis 时就可以使用 bottom-up 的方法(称为 “bottom-up evalutation”)。
Inherited Attributes:总是通过 parse tree 中的父结点 / 兄弟结点的 attributes 计算 / 解析而来的属性。
这种属性一般在 top-down evaluation 中才会使用。
3.3.1 Semantic Actions in Bottom-Up Evaluation
Bottom-Up Evaluation 通常和 Bottom-Up Parsing(LR Parser)一起使用。
我们举个例子来阐述用 Bottom-Up Evaluation 来解析 Semantic Rules 的方法。
假设一棵 parse tree 中包含了一个 production
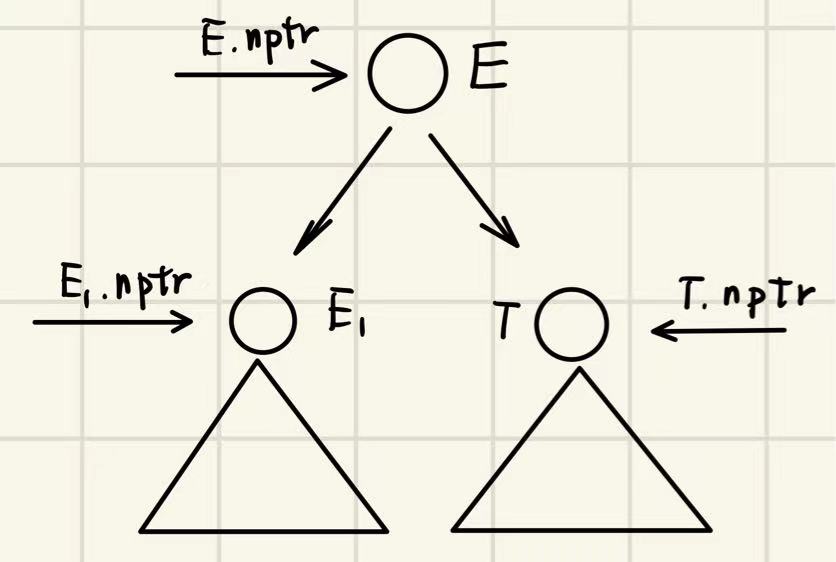
我们对这些 non-terminal 定义一个 synthesized attribute:nptr,记 E.nptr、E1.nptr、T.nptr 分别为指向 AST 中对应结点的指针的值。
这个 attribute 的目的是,为了结合 parse tree 中的语法(CFG)和语义规则(semantic rules),来构建一个 AST 框架。
有了这个 attribute,我们可以将一个 CFG 中的 production 对应一个 semantic rule(创建 AST 的规则),如下:
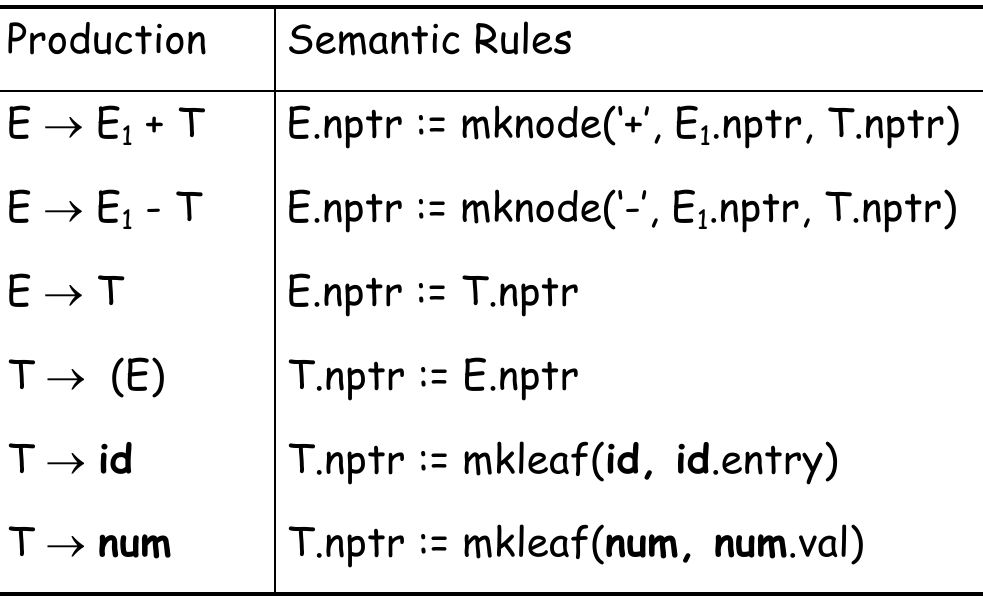
注意到
,对应的 semantic rule 为 E.nptr := T.nptr,相对于 parser tree 进行了压缩;
那么还有哪些更多的 attributes(如上面的 .entry / .val)?
另两个 synthesized attribute 定义为 val、lexval,记 terminal.lexval 为这个 terminal 它的实际 token value 的值;记 symbol.val 为这个 symbol 在上下文中实际的值。
这两个 attributes 的目的不言而喻;
它们同样可以由 production 对应出 semantic rules:
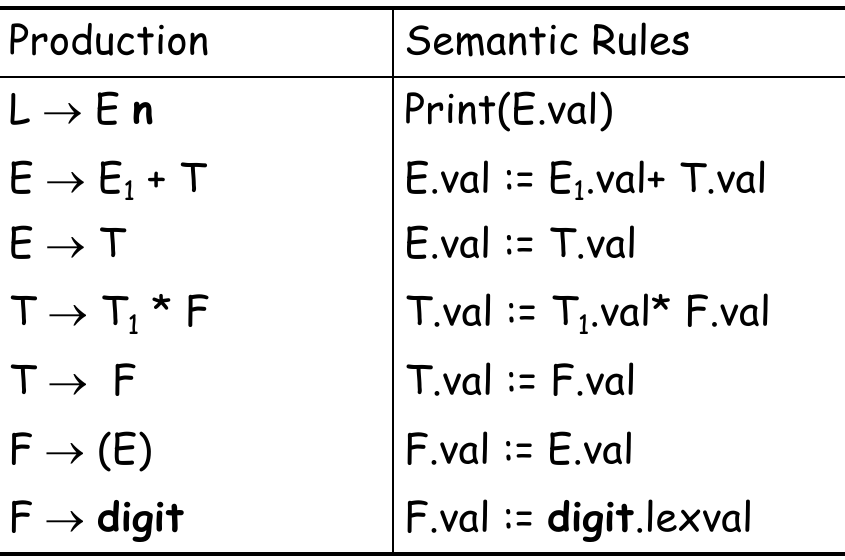
例如,对 3 * 5 + 4 这个输入,通过词法、语法解析后,我们可以在语法解析中利用上面定义的 val/lexval 的 attributes 和 semantic rules,生成这样的 decorated parse tree:
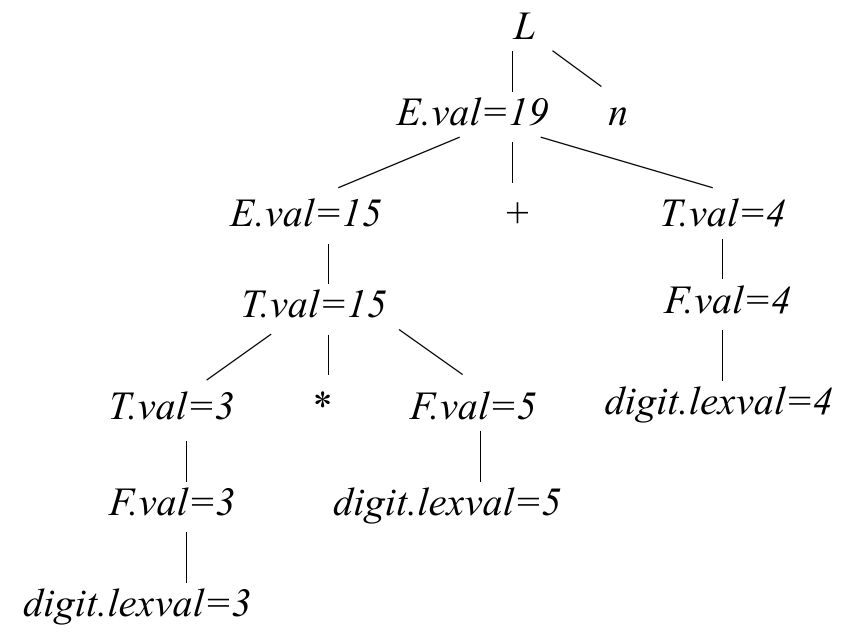
3.3.2 Semantic Actions in Top-Down Evaluation
我们用自动化工具几乎都是通过以上的 Bottom-Up Evaluation 的方法来做 semantic actions 的。
而这种 top-down semantic evaluation 的方式通常和 top-down parsing(LL(k) Parser)一起使用。我们之前讨论了 top-down parser 没法处理左递归、不左分解的情况,但历史上有些人手写的 parser 就是 top-down 处理的方式。
而且 top-down evaluation 更适合手写,而不是自动化生成。
3.4 Example of Semantic Action: The AST of Tiger Language
我们以 Tiger Language 为例,介绍一下 Tiger 语言的 AST 应该如何构建。
3.4.1 What about Error Positioning?
注意一件事,如果我们的 tiger 程序存在 syntax/semantic error,那么还是需要抛出的。那么这个错误的位置如何知晓?
我们知道错误在源文件中的位置只有词法分析器能知道(因为此后处理的不再是原文件了),而词法分析器最后的 curTokenPosition 停在 EOF 的位置,是没法提供有效信息的。
因此,为了让语法/语义阶段出现的错误能正确地提示在指定的位置上,我们需要对词法分析器、语法分析阶段加点东西:
在 parser generator 中同时维护一个 position stack,与 semantic value stack 对应;
这样每个 token 的起始、终止位置以及所处的阶段等信息就能在 semantic actions 中使用,如果出现错误就能得知错误的位置了。
这就需要 syntax analysis 和 semantic analysis 两个阶段联动,这对于合在一起的 bison 来说就能实现,而 yacc 就没有实现。
3.4.2 Tree Node Types
Tiger 中需要哪些种类的 AST Node 结点?
表示变量的结点:
SimpleVar(x普通变量)、FieldVar(f.x的域变量名x)、SubscriptVar(b[x]的下标变量名x);表示表达式
VarExp、NilExp、IntExp、StringExp、CallExp、OpExp、RecordExp、ArrayExp;以及:
SeqExp、AssignExp、IfExp、WhileExp、BreakExp、ForExp、LetExp;声明语句
FunctionDec、VarDec、TypeDec;FunctionDec支持互递归函数声明(Mutually Recursive Functions),如下:xxxxxxxxxxletvar a :=5function f() : int = g(a)function g(i: int) = f()inf()end因此它本身的定义是一个
FundecList,额外使用了两个类型Fundec(描述一个声明的具体签名)、FundecList(这些声明的定义列表);同样
TypeDec支持互递归声明(Mutually Recursive Declarations),如下:xxxxxxxxxxtype tree = { key: int, children: treelist }type treelist = { head: tree, tail: treelist }因此它本身使用了
NameAndTyList,并且额外利用了NameAndTy(描述一个类型声明)、NameAndTyList(这些类型声明的列表);类型定义
IntTy、StringTy、NilTy、VoidTy、NameTy、RecordTy、ArrayTy;结构体(域)
Field、FieldList;表达式列表
ExpList;操作符
xxxxxxxxxxenum Oper {PLUS_OP, MINUS_OP, TIMES_OP, DIVIDE_OP, EQ_OP, NEQ_OP, LT_OP, LE_OP, GT_OP, GE_OP};其他辅助结点:
DecList、EField、EFieldList;
以及需要将词法分析器给出的 token 与 unique syntax symbol 对应起来的 Symbol(和 Symbol Table),实现在 symbol 和 string 间相互转换的功能;
注意有几个 tricky 的点:
短路运算直接用
if then else实现,例如e1 & e2被语法分析转换为if e1 then e2 else 0;e1 | e2转换为if e1 then 1 else e2;一元运算符
-直接用二元运算符-实现:-i被语法分析转换为0 - i;
这样可以让 AST 更简单一些;
3.4.3 Symbolic Table & Nested Function
需要注意 Tiger 支持将 local variable 用在嵌套函数中。这个特性有点像 JavaScript/TypeScript 而不像 C,例如:
xxxxxxxxxxfunction f(a: int, b: int) { function g(): int { x: int = 0; return x + a; }}这就意味着这个变量 a 必须放在内存中,而不能位于寄存器上。在 C 中出现这种情况的只有用到 & 取地址。
于是我们需要在 VarDec(局部变量 escape)、Field(函数参数 escape) 中使用 bool escape_component 指示这个变量是否需要放到内存中(默认 TRUE 一直需要),然后只有发现这个变量被用在 nested fucntion 中(称为 “escape analysis”)才改成 FALSE;
但是对 field 中的 record,虽然可能 escape,但由于 field 中存放的是引用(指针),因此不需要 escape_component;
3.EX Bison: The tool to generate AST from SDD
我们以 Bisonc++ 为例。它主要会输出以下内容:
基类头文件(可以被 lexical scanner 包含,其中可以定义共用的 token 符号);
一个 Parser 类的头文件,定义了 Parser 的基本接口;
一个用于实现的头文件(仅用于 Parser 内部实现);
一些 Parser 的成员,包括实际读取 grammar rule files(简称 grammar files,我们需要定义的 CFG 存放的文件)的实现函数;
我们接下来介绍如何以 Bisonc++ 指定的格式来编写 CFG 规则,也就是 Grammar File。
和 Flexc++ 的 rules file 类似,bisonc++ 的 grammar file 构成如下:
xxxxxxxxxxBisonc++ directives%%Grammar rules
3.EX.1 Bisonc++ Directives
在 directives 中,主要的任务就是 定义 terminals/non-terminals 的名称、描述运算符优先级和结合性、各种 symbols 的数据类型的 semantic values(类型的语义值就是语言定义的抽象语法树的结点类型),等等。
xxxxxxxxxx%baseclass-preinclude pathname // 定义了需要被包含的头文件%class-name parser-class-name // 定义 parser 类名%default-actions off|quiet|warn|std // 是否使用默认的 semantic action($$ = $1)%error-verbose // 发生错误时打印 parser 的 state stack%include pathname // 立即将另一个指定文件的规则引入到当前位置(可以用于分 grammar files)%left/right/nonassoc [<type>] terminal(s) // 定义 token 的优先级和结合性 (type 有尖括号,需要是类型的 semantic value)%negative-dollar-indices // 是否使用负数索引 $%prec token // 指定 token 覆盖原先的优先级和结合性(在 unary minus 负号的定义中有用)// https://fbb-git.gitlab.io/bisoncpp/manual/bisonc++04.html#l36%print-tokens // 自动实现 Parser::print_,打印出当前解析的 tokens%required-tokens ntokens // error recovery 中,防止语法分析或语义分析中因为一个错误带来很多错误,可以容许 ntokens 间出现的错误不抛出%scanner header // 指定 Lexical Scanner 定义的文件头%stack-expansion size // 指定 semantic value stack 在加入多少元素后就需要扩大%start: defining the start rule // 指定开始符号(默认第一条 rule 为 start symbol)%token [ <type> ] terminalToken(s) // 定义 token 语义类型(关键字之类的就不需要)、terminal 表示 以及 名称间的关系// type 必须要是 %union 中定义的 semantic value// token 名称不能以下划线结束,不能是被 bison 内部使用的名称,例如 ABORT, ACCEPT, ERROR%type <type> symbol-list // 将 semantic values 和指定 symbol 绑定起来,常用于声明 CFG 的符号,将它们和类型关联%union union-definition body // 定义一组 semantic values// 将 grammar rules 中用到的 semantic values 和 parser 的 AST 结点类型联系起来// %stype, %union 和 %polymorphic 是互斥的,因此只介绍这种%baseclass-header filename%class-header filename%filenames filename%implementation-header filename // 这 4 条指令指定了 bisonc++ 输出文件的名称
3.EX.2 Grammar Rules
grammar rules 的部分就是在做两件事:定义 CFG productions,以及对应的 semantic actions(如何将 terminals 构建成 non-terminals,如何将 non-terminals 构建成 AST);
我们在这里可以使用的 token 要么是 literal character token,要么是在 directives 中定义过的 tokens。
语法如下:
xxxxxxxxxxlhs:production_rhs;// 和 CFG 一样,也可以多条 productionlhs:production_rhs1|production_rhs2|...;// 在 production 后用 {} 定义 semantic actionlhs:production_rhs1|production_rhs2{// C++ statements here}// production rule 可以为空 (ε),指可以匹配任何结果,但不被这条规则处理
在 semantic actions 中,我们可以使用 $$、$number 这样的预设符号来指代 production 中对应的 symbol 的 semantic value。例如:
xxxxxxxxxxexp:...|exp '+' exp{// lhs 的 semantic value 为 $$// rhs 中从左到右第 i 个 symbol 的 semantic value 为 $i// 注意 action 需要符合我们之前在 directives 中关联的 symbol 类型的 semantic value$$ = $1 + $3;}|...
上面的 $number 这样的预设符号,其实就是在取 Parser 维护的 semantic value stack 中的数据。
然后之前提到的 positioning stack 其实在 bison 中可以作为 attribute 的一部分,在从 lex 中取的同时,构造 AST 结点并且都放到 state stack 中。
3.EX.3 Basic Grammatical Constructions
这里列举一些 CFG 的书写的常见模板和思路。
xxxxxxxxxx// simplest expressionexpr:ID|NUMBER;// C++ style string concatenationstring:STRING|string STRING;// comma-separated listvariables:IDENTIFIER|variables ',' IDENTIFIER;// simplest nested blockexpr:NUMBER|ID|expr '+' expr|...|'(' expr ')';
3.EX.4 The Generated Parser Class' Members
这里仅列举一些可能用到的成员。
xxxxxxxxxxprivate:
size_t stackSize_() const;// 返回当前 parser state stack 中元素数量
size_t state_() const;// 返回当前 parser 的状态
bool Base::recovery_() const:// 当 parser 进行 error recovering 时返回 true
int Base::token_() const:// 当前 parser 正在考虑的 token
3.5 Semantic Analysis
前面我们通过向 parse tree 中添加 attributes(.nptr、val、lexval),并且利用 semantic rules 构建了基本的 AST,现在我们要遍历这个 AST,并且用额外的上下文相关信息进行诸如类型分析、作用域分析的工作,向 environment table 添加数据,检查 AST 的合法性,并为翻译阶段做准备。这就是 Semantic Analysis。
3.5.1 Scope Information, Binding Information, Environment
Semantic Analysis 首先需要分析变量作用域的上下文信息(Scope Information)。
首先每个变量有一个作用域(可见范围),例如:
TIGER 语言中的 LET 语句
let D in E end,在
当这个作用域结束后与这个局部作用域绑定的变量就需要被抛弃;
如果存在嵌套的作用域,例如:
xxxxxxxxxxlet D1in let D2 in E2 end E1end设在
此外,Semantic Analysis 还需要分析变量类型的上下文信息(Binding Information)。
编译原理中,把 binding 认为是给予 symbol 一个含义和类型(将一种数据类型,即变量名字符串,和另一种数据类型,即类型枚举,绑定起来。因此有类型绑定的说法),而所谓的环境(environment)就是一组 bindings 的集合,存储环境的数据结构就称为 environment table(或 symbol table)。于是我们发现,可以用环境这个集合来描述一个作用域!
例如一个环境
一个 identifier 名称为
一个 identifier 名称为
其他类型的 ID token 都被认为是 undefined variables;
有了环境,我们就可以在语义分析时,每次遇到一个 name 时检查一次 environment table、每次出现新的 name 或者是关于已 name 的更新的信息时,可以更新 environment table。这个表可以为之后 code generation(例如生成 label)、data layout(是否在栈上/寄存器上、数据需要预留多大位置等等)提供依据。
那么 environment table 的组织形式应该是什么样子的?在 AST 中,以一个函数符号为例,它实际上是一个指向 Symbol Table 一个 Entry 的指针组成的数据结果。同样,一个类型也是以符号的形式呈现。
而我们最好不要在这个数据结构中直接指向类型,而是用一个链表保存起来。
3.5.2 Implementation of a Environment Table
xxxxxxxxxxfunction f(a: int, b: int, c: int) = ( print_int(a + c); let var j := a + b var a := "hello" in print(a); print_int(j) end; print_int(b);)假设在解析上面的 Tiger 语言代码时,进入函数前的初始环境
进入函数体解析:
LET 语句的
LET 语句的
LET 语句全部结束后,环境重新回到
函数体结束后,环境回到
如何实现这种环境的切换?
Functional Style:保留
的同时创建 ; Imperative Style(祈使命令式):
变为 通过直接修改内容实现,当 存在时, 相当于被销毁;恢复时 undo(可以维护一个 undo stack)。也就是任何时刻只有一个 environment table; 这两种 environment management 的方式和要编译的语言是没有关系的。
Imperative
考虑了这些问题,我们可以开始实现一个 environment table 了。我们以 imperative style 为例。
imperative environment table 不过记录了symbol(指向 symbol table 的 entry)和类型的映射,因此可以选用 Hash Table(以 name 字符串作为 hash key);
考虑最简单的 Open Hash Table: Bucket + Linked Lists。总体来说比较高效,删除元素快速。
而且这样还能自动适应环境嵌套覆盖(优先级)的语义:每次更新声明时,在以前的 linked list 前插入(因为是按 name 为 key,所有同一个 variable 必然位于一个 bucket 中),这样从前向后查找 environment table 时只能找到最新最内声明的变量。
然后我们需要实现 undo stack。人们想了一个巧妙的方法,不需要额外建一个数据结构,直接在每个 environment table 的 entry 中加一项 next_in_stack,然后以一个额外的栈顶指针保存最近插入的 entry,不就行了?这就相当于是一个 linked stack!结构如下:
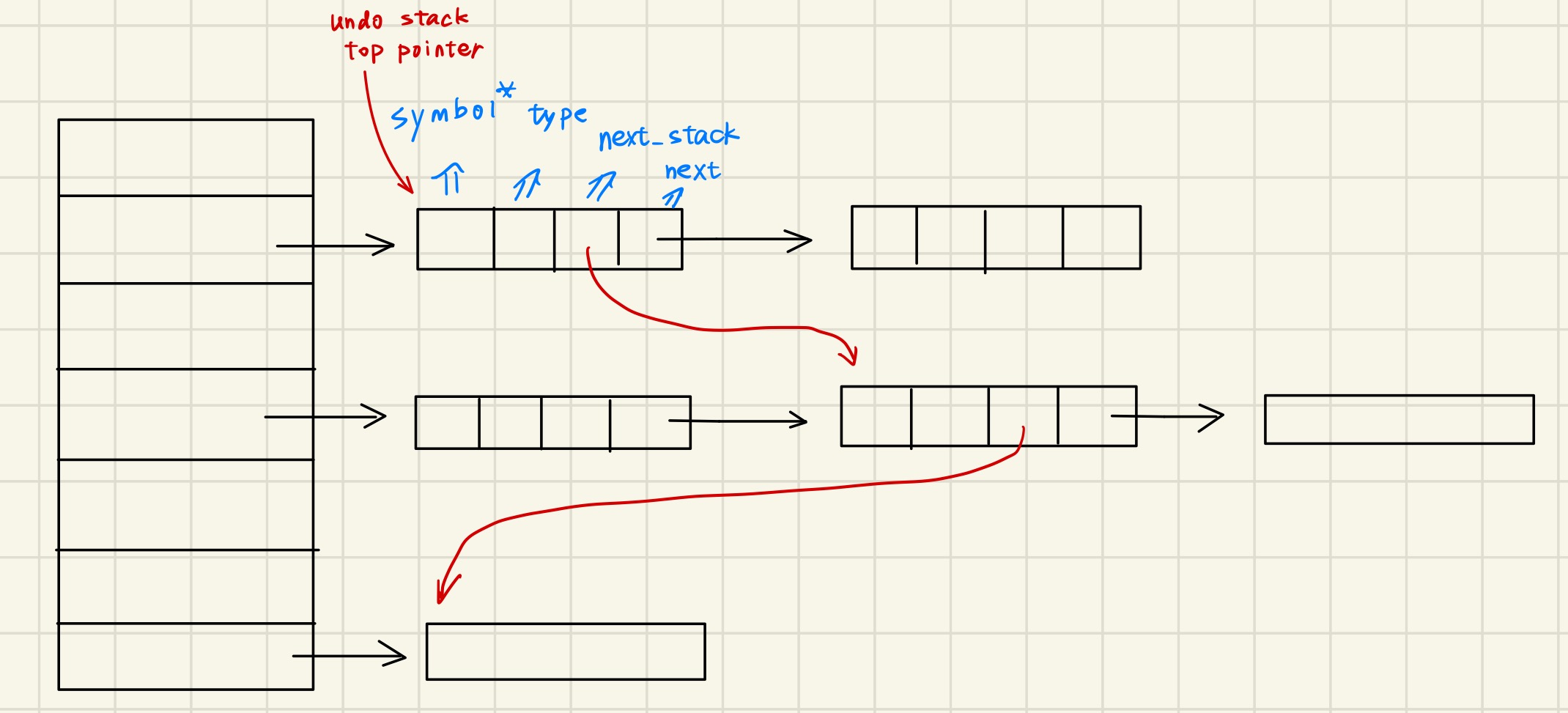
你可能会问,这种方法好像没有明确标注栈中的哪些 bindings 是属于最新的 scope(environment),哪些是上一个的。如果不知道这个的话那么退出当前 scope 的话就不知道要 pop 掉几个 bindings 了!
因此我们需要每次进入一个新的 scope 时,向栈中插入一个并不在 Environment Table 中的特殊的 “Mark” Symbol,表示这是新的 scope 的开始,下次退栈退到这个特殊的 mark 后停止就行。
Functional
Functional environment table 也可以使用同样的 Hash table 完成,只不过:
每次进入新的作用域后直接 copy 表,仍然共享 old buckets;
并且加入 new bucket 时直接在新表上做操作,不对原表做破坏性操作;
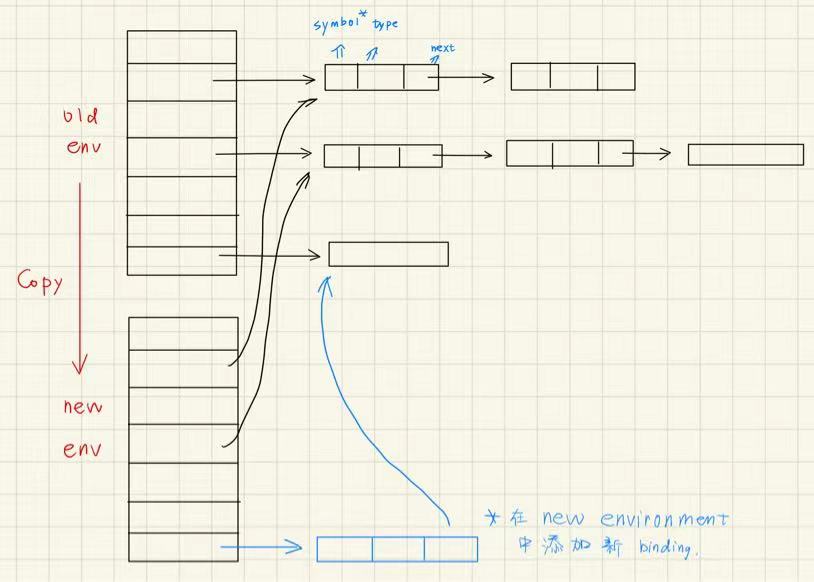
这样做的坏处是 non-destructive update 不高效、每次创建新表空间利用率低下。
因此我们改进后使用 Binary Search Tree:
如果需要在深度为
这样插入和查找一样高效,并且是个可以持久化的数据结构。如下图所示:
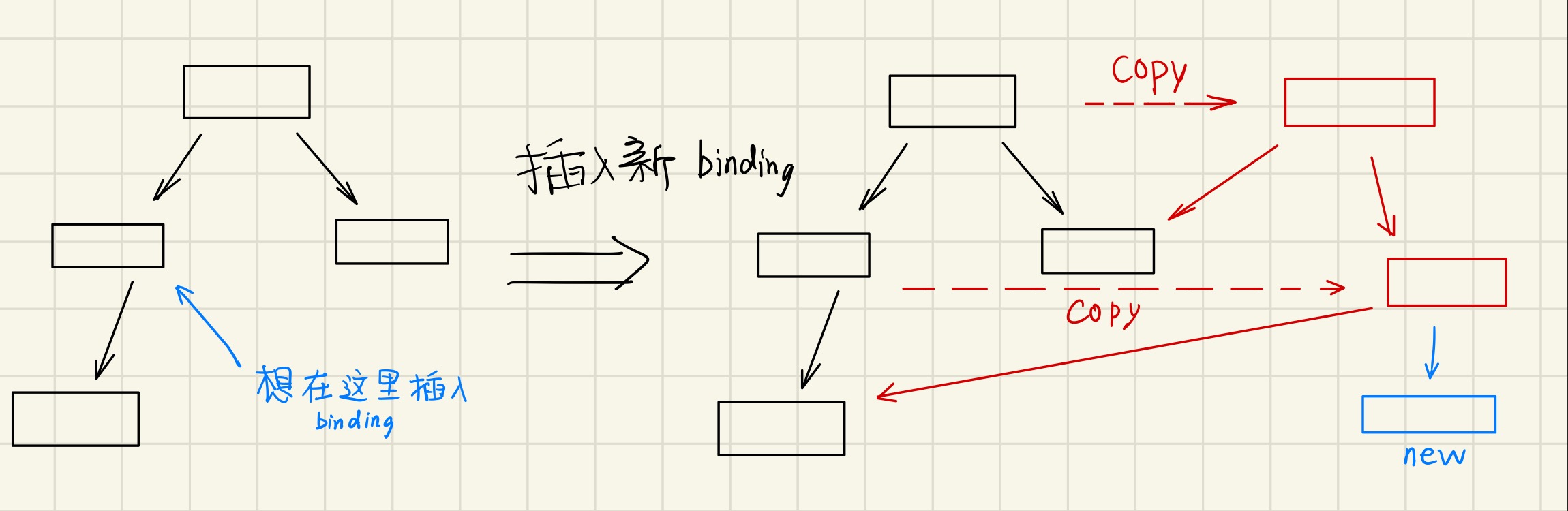
这个 copy 的思想和 Copy-On-Write 很像。
Sidebar:有些语言可能需要有多个 environment table 同时有效,它们往往需要每个模块 / 类 / 记录都有一个自己的 environment table。
例如 ML 语言:
xxxxxxxxxx# sigma0structure M = structstructure E = struct # sigmaM1 = { E |-> sigma1 } U sigma0val a = 5; # sigmaE = { a |-> int }endstructure N = structval b = 10; # sigmaN = { b |-> int, a|-> int }val a = E.a + b; # sigmaM2 = { N |-> sigmaN } U sigmaM1endstructure D = structval d = E.a + N.a; # sigmaD = { d |-> int }end # sigmaM3 = { D |-> sigmaD } U sigmaM2end再例如 Java:
xxxxxxxxxxpackage M; // sigmaM0 = sigma0class E { // sigmaE = { a |-> int }static int a = 5; // sigmaM1 = { E |-> sigmaE } U sigmaM0}class N { // sigmaN = { b |-> int, a |-> int }static int b = 10; // sigmaM2 = { N |-> sigmaN } U sigmaM1// 允许先使用后定义(forward reference)static int a = E.a + D.d;}class D { // sigmaD = { d |-> int }static int d = E.a + N.b; // sigmaM3 = { D |-> sigmaD } U sigmaM2}最终
都使用 的范围(同一个 package);
3.5.3 An Example: Bindings in Tiger Language
在 Tiger Language 中,我们可以定义个 Binder 类型,专门用于存放一个 environment table 的 entry 的内容(key、value、next、prevtop),然后再使用 Table 类型来构建 Hash Table 并管理这些 entries;
实际上,为了方便管理、搜索 environment,我们习惯将类型、值的 binding 放在不同的 environment table 中。
Type Binding:遇到一个 type identifier,放到专门存放 symbol 和类型映射关系的 environment table(type environment)中;
有一点需要注意:在解析开始前将
int / string这种类型符号先与IntTy、StringTy类型 bind 起来(构建注:AST 中的
absyn::Ty是符号,而type::Ty才是需要解析并存放到 Environment Table 中的类型;Value Binding:遇到一个 value identifier,它可能是一个 variable 或 function;
如果是一个 variable,需要判断其类型;
如果是一个 function,需要判断其返回类型、参数类型;
为了实现 value binding,构造
EnvEntry(子类VarEntry、FunEntry),并且将这些 Entry 管理在另一个 Environment Table(value environment)中;同样需要注意:在解析开始前将
flush / ord / chr / size这样的标准库函数定义,或者其他的预设变量的定义先与 AST Node bind 起来;
3.5.4 Another Example: Type-Checking in Tiger Language
Implementation Examples
有了前面的 semantic actions 的铺垫,我们现在可以通过遍历 AST、检查树上的各个结点,并且填写 type/value environment table,其中顺便检查作用域和类型的合法性。
比如我们可以这么定义 semantic analysis 的调用接口:
xxxxxxxxxxclass Exp/Dec/Var {// ... virtual type::Ty *SemAnalyze( env::VEnvPtr venv, env::TEnvPtr tenv, int labelcount, err::ErrorMsg *errormsg ) const = 0;// ...}很明显 venv 和 tenv 的作用是方便在遍历 AST 时到当前的结点时,向 environment tables 中加入 bindings;
labelcount 的作用则是在 semantic analysis 时检查 BREAK 关键字是否处于 for / while 的循环中。
最终 errormsg 则是提供错误发生的详细信息。
我们以 OpExp 的 Semantic Analysis 为例:
xxxxxxxxxxtype::Ty *OpExp::SemAnalyze(/*...*/) const { /* 递归 OpExp 左右两边的解释式,进行类型检查并获取其类型 */ type::Ty *left_ty = left_->SemAnalyze(/*...*/)->ActualTy(); type::Ty *right_ty = right_->SemAnalyze(/*...*/)->ActualTy();
/* 四则运算 和 短路运算 只允许是整型 */ if (oper_ == absyn::PLUS_OP || oper_ == absyn::MINUS_OP || oper_ == absyn::TIMES_OP || oper_ == absyn::DIVIDE_OP || oper_ == absyn::AND_OP || oper_ == absyn::OR_OP) { if (typeid(*left_ty) != typeid(type::IntTy)) { errormsg->Error(left_->pos_,"integer required"); } if (typeid(*right_ty) != typeid(type::IntTy)) { errormsg->Error(right_->pos_,"integer required"); } return type::IntTy::Instance(); } /* 其他运算(比较运算等)需要类型相同就行,返回的一定是 integer */ else { if (!left_ty->IsSameType(right_ty)) { errormsg->Error(pos_, "same type required"); return type::IntTy::Instance(); } } // 无论是否出错,都返回正确的类型,继续解析 return type::IntTy::Instance();}再比如 LetExp:
xxxxxxxxxxtype::Ty *LetExp::SemAnalyze(/*...*/) const { // 值得注意的是,这里进入一个新的 scope 时调用 EnvTable 插入 Mark 以便管理 scope entries venv->BeginScope(); tenv->BeginScope(); // 声明的类型虽然用不到,但还是需要检查一遍 for (Dec *dec : decs_->GetList()) dec->SemAnalyze(venv, tenv, labelcount, errormsg); type::Ty *result; if (!body_) result = type::VoidTy::Instance(); else result = body_->SemAnalyze(venv, tenv, labelcount, errormsg); tenv->EndScope(); venv->EndScope(); return result;} 或者 SimpleVar:
xxxxxxxxxxtype::Ty *SimpleVar::SemAnalyze(/*...*/) const { // SimpleVar 作为 Value 应该在 Value Environment 中查找 env::EnvEntry *entry = venv->Look(sym_); if (entry && typeid(*entry) == typeid(env::VarEntry)) { // 注意到需要 Type::ActualTy(),因为可能这个变量的类型是用 Type ID(type 自定义)描述的 // 在定义 type::NameTy 时重写 ActualTy() 即可 return (static_cast<env::VarEntry *>(entry))->ty_->ActualTy(); } else { errormsg->Error(pos_, "undefined variable %s", sym_->Name().data()); } return type::IntTy::Instance();}如果是对于 VarDec,那么大致需要:
解析 expression 的类型;
如果存在 type hint,则比较类型是否一致;
如果 expression 是
NilTy,那么要求 type hint 必须是RecordTy;返回解析好的 type;
About Recursive Definitions (Self & Mutual)
对于 FuncDec,大致需要:
解析返回值类型;
对参数
FieldList构建TyList(MakeFormalTyList,遍历typ_(在Field中是 Symbol) 然后解析并放入TyList);用返回值类型和参数
TyList构造FunEntry并加入 Value Environment Table 中。接下来继续解析函数体;为 Value Environment Table 启动一个新的 Scope;
在新的 scope 中,利用解析参数的
TyList和各个参数符号name_,依次向 Value Environment Table 中插入参数的类型 bindings;最后对函数体 expression 调用
SemAnalyze并检查返回值类型是否匹配;最终结束这个 scope;
但是如果需要考虑递归定义,那么这么写是会出问题的(函数体解析时会出现 undefined symbol),因此需要:
将
FuncDec的解析拆成两个部分,第一部分 1-3 节课解析函数签名并将函数体的解析留空,第二部分 4-7 节解析函数体;等到一组
FuncDec中的所有签名全部解析完成,再使用新的 Environment Tables 进行第二部分的解析;
对于 TypeDec,如果不考虑递归定义,只需要:从声明列表中取出声明表达式然后调用 absyn::Ty::SemAnalyze,最后加入 Type Environment Table;
其中
absyn::Ty::SemAnalyze的作用是将absyn::Ty(AST 结点上的符号)解析为type::Ty(编译器存放在 Type Environemnt 中的类型);如果遇到
absyn::RecordTy,则会递归地解析;
如果考虑到递归定义,则需要对 absyn::RecordTy::SemAnalyze 单独处理:
将
type tid =这部分看作 header 先解析,并将不完整的信息填入 Type Environment Table,例如:xxxxxxxxxxtenv->Enter(name_, new type::NameTy(name_, nullptr));在
TypeDec遍历完一遍后,再遍历一次,逐一解析类型的 body;这个时候 body 的类型一定可以从 Type Environment Table 中找到(即使它们的 body 可能是空的,毕竟用不上);
在 TypeDec 中,和 FunDec 不同的是,FunDec 是递归(互递归/自递归)调用,而 TypeDec 是递归定义,因此需要考虑 “定义递归圈” 的问题:
也就是说,只有 Array 和 Record 的类型定义允许形成 “递归圈”(因为在底层的 C++ 中它们用指针实现),其他类型的定义只能普通定义,或依赖定义。
例如:
xxxxxxxxxxtype cell = { info: int; next: cell } // record 自递归type a = { entry: b; info: int }type b = { entry: a; info: int } // record 互递归是允许的,但是下面的就不允许:
xxxxxxxxxxtype cellEntry = cellEntry // 普通类型自递归无效type a = btype b = ctype c = a // 普通类型互递归无效
Name or Structural Equivalence
此外,TypeDec 还要关注采用 Name Equivalent 还是 Structural Equivalent 的问题。
例如:
xxxxxxxxxxlettype a = {x: int, y: int}type b = {x: int, y: int}var i: a = ...var j: b = ...in i := jend
这个表达式是 illegal 的。
这证明 Tiger Language 实现采用 Name Equivalence,强调类型名称作为类型的最终标识;
另一种 Structural Equivalent 的实现,指只要两个类型定义的结构一致就是相同类型(像上面的表达式就应该是 legal 的),这个实现起来比较复杂。
更明显一点,Tiger Language 不支持 Structural Equivalent,因此下面的解析式也是 illegal 的:
xxxxxxxxxxlettype a = { x: int, y:int }type c = avar i : a := ...var j : c := ...in i := jend
如果一个语言想要支持 Structural Equivalent,那么算法如下(不以 Tiger Language 为例):
可以定义 non-primitive types:
array [] of T、T1 x T2(结构体{a: T1, b: T2}的简记)、*T1(pointer)、T1 -> T2(函数简记);
判断结构类型的方法:
xxxxxxxxxxint sequiv(s, t) { if ( s and t are the same basic type ) return 1 ; /* 基本类型直接比较相同 */ else if ( s == array(s1) && t == array(t1) ) /* 如果都是数组,直接比较元素类型 */ return sequiv(s1, t1) ; else if ( s == s1 x s2 && t == t1 x t2 ) /* 如果都是结构体,递归比较结构体中每一个成员的类型 */ return sequiv(s1, t1) && sequiv(s2, t2) else if ( s == pointer(s1) && t == pointer(t1) ) /* 如果都是指针,比较指针指向的数据类型 */ return sequiv(s1, t1) else if ( s == s1 -> s2 && t == t1 -> t2 ) /* 如果都是函数,比较参数和返回值类型 */ return sequiv(s1, t1) && sequiv(s2, t2) return 0;}
Type Conversion
很多语言支持类型转换。考虑下面几种类型转换:
隐式类型转换(不存在信息丢失):
int转double等(反过来不行);运算转换,如
int + real;
显式类型转换;
具体实践也很简单,举个例子:
见到 integer 常量(不含小数点),认定为
int类型;见到含有小数点的数,认定为
real类型;见到是一个 ID Token,从 Value Environment Table 中查;
见到一个二元运算表达式,两个操作数类型相同则好办,类型不同可以指定一些规则,例如有一方为
real则结果为real;
General Overloading
一个语言应该如何实现重载(例如运算符为首的符号重载)?
Determine a unique meaning for an occurrence of an overloading symbol;
Well known as operator identification;
上面通过特殊用法来实现重载,被称为 simple overloading。它的实现很简单,加一条语法规则不就行了!
而如果使用方法一样,但是操作的类型不一致,则被称为 general overloading;例如 C++ 中字符串加法(std::string)和整型加法的使用是一样的;
它的含义就要取决于 context 了,需要我们在做 Bottom-Up Scanning 时留意 context,回来构造某个 operator 的真实定义。这需要更复杂的算法实现。
Chapter 4. Translations
在 Semantic Analysis 过后(生成 AST + Environment Tables),编译前端(compiler front-end)的工作基本结束。
接下来一步是 “翻译”,它的主要工作是:生成机器相关的栈帧布局、以及 IR 树(Intermediate Representation Tree),为了之后汇编为目标平台的机器做准备。
我们从 4.1 ~ 4.5 对 Translation 进行必要的准备和补充,4.5 以后介绍如何具体进行 Translation。
我们一步步看翻译的运作原理。首先是如何生成机器相关的栈帧布局。
4.1 Activation Records
我们知道,在 C 语言中的栈帧分配(局部变量)完全由编译器进行分配回收的管理。并且,对于静态变量/函数,编译器需要符号重命名,并且需要打上标记,准备由 Assembler 将它们写到 .text / .data 中。
前者的栈帧分配情况就需要在 translation 阶段完成。
要优雅地分配栈帧,我们首先了解一个机制 “activation records”(活跃记录)。
我们定义:
过程
P的活跃(activation):对于一个过程(procedure)P的调用(invocation)就是P的一次活跃;过程
P的生命周期(lifetime):指在P过程中执行P时的所有步骤(包括被P调用的 procedure);变量
x的生命周期:指一个变量在被定义的作用域中所能执行的片段。例如一个变量在某个函数中被定义,那么这个变量的生命周期就是这个函数的生命周期。
变量的 “生命周期”(lifetime)和 “作用域”(scope)需要区分开,前者是 run-time 的动态的概念,后者是静态的概念;
另一方面,在很多架构的机器上(例如 x86/ARM/RISC-V),栈总是从高地址向低地址增长的。
而在这个栈上,我们编译器管理的变量,或者函数的 “帧”(frame),其实在这里都被称为 activation record(变量或者函数的活跃记录)。
现在回想之前的知识是否有种串联起来的感觉?
程序在栈上管理的函数栈帧(例如 x86 上,一个函数栈帧第一个 entry 是 return address,上一栈帧的最后几个 entries 是 parameters)、管理不取地址的局部变量(直接用 %rsp 分配的部分),在编译器的角度看,就是一个函数或者变量的活跃记录,在它们的生命周期中需要保持这些记录以维持程序正常运作。
也就是说,编译器需要在这个阶段就确定下来栈帧的布局,在生成代码时也按照这个设计模式来管理栈帧和相关寄存器的使用。
当然,一个 organization 的设计不是必要的,只是说,遵循一个 organization 的设计能提升执行速度、简化编译器在代码生成的逻辑。
这里需要确定一下一个语言的函数(上面所说的 “过程” 的具体表达)的特征:
Function-valued variables:是否能赋给一个变量?
Nested:这种语言的函数是否可以嵌套定义?
Returnable:这种语言的函数是否有返回值?
在 Pascal/Tiger Language 中,函数是 nested,但不是 returnable 的(因为 tiger 是将函数体作为一个表达式处理的,直接作为一个特殊的变量);
而在 C 中,函数是不能 nested 的,是一个 returnable 的过程;
而 ML 语言、Scheme 语言、Python 语言等等,它们的函数既是 nested,又是 returnable 的,它们都被称为 “Higher-order function”(高阶函数,同时支持两种及以上上述特征);例如 Python 的闭包就是一种高阶函数:
xxxxxxxxxxdef f(x: int):def g(y: int) -> int:return x + yreturn g
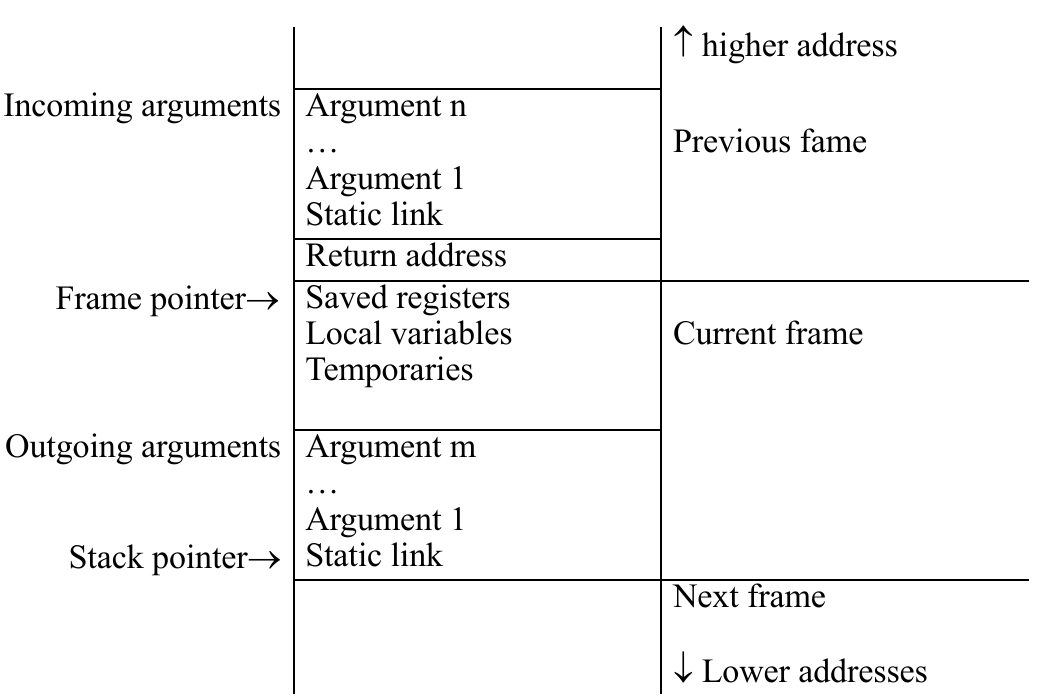
上图就是 Tiger Language 设计的栈帧布局(或者称 AR Layouts),注意到我们留了一个 Static Link 作为函数传递的真正第一参数。它实际上是编译器自己加上去的,为了处理 Tiger Language 函数嵌套定义(nested)的情况。
4.2 Registers & Frames Allocation
实际上很多语言的编译器都是尽可能将 frames 保存在寄存器中,这样能加快执行速率。
尤其是函数参数和返回值,像 RISC 架构大都将返回值放在寄存器中;
常用的本地变量、临时变量更是如此;
4.2.1 Function Frames
我们先讨论函数的栈帧分配。将语言对函数的实现分为以下几类(注意不是一个语言里面的传参方法,而是一个语言函数参数传递的设计方法):
Call-by-Value
如果一个语言的函数是按值传递参数的,那么它们的参数可以直接被处理成 local name(local variable),和局部变量一样,可以放在栈上(而不用担心降低性能);
传递参数时(例如
意思是,在执行过程中不影响 caller 栈帧中传入的变量,只是修改自己栈帧上的局部变量;
Call-by-Reference
对于按引用传递参数的语言,我们实现起来也比较简单,让这个传递的参数必须位于栈上,然后提供一个指针就行。
但是如果参数不是左值(例如
意思是,在执行过程中一直修改的是 caller 栈帧中传入的变量;
Call-by-Restore
一种混合 call-by-value 和 reference 的方法是 call-by-restore(也称为 “Copy-restore linkage” 或 “copy-in copy-out”);
它的实质还是 call-by-reference 的一种实现形式,但是会更节省一点(右值不需要强制再创建一个新的帧了):
如果传入的是右值,就直接作为 local variable(相当于值传递);
如果传入的是左值,那么先像 local variable 一样 copy 一遍在本地栈帧,此后修改这个 local variable,直到最后 return 时写回原来的地址(还是相当与引用传递,但在返回前都是不变的);
这种方法现在设计的编译器不太使用了。
Function: Call-by-Name
传进去的参数会直接被看作 symbol name 处理,最常见的设计的就是 C/C++ 中的 macro。
4.2.2 Function Parameter Passing
传递函数参数的方法,RISC 架构都选择在寄存器上完成,前
老式架构因为兼容性就需要都在栈上传递(例如 x86。而在 x86-64 上吸取 RISC 经验,前 6 个参数从寄存器传递),但这会有比较大的 memory traffic 以及性能问题;
但实际上是 memory traffic 不会因为寄存器传参而减少。考虑这个函数:
xxxxxxxxxxvoid P(int a, int b) { return Q(b) + Q(a);}我们知道 a 一开始是保存在第一个参数寄存器上的,但是在 P 内调用 Q 时,由于 calling convention,参数寄存器还是需要把 a 备份到栈上;
你可能会说,我们可以把 a 转移到其他寄存器上,真实情况像 GCC 这样的编译器确实也会这么做。要么选 caller-saved registers(不需要备份),要么选 callee-saved registers(需要备份到栈上);
如果中间没有掉其他函数的话,可以使用 caller-saved 无需备份。但是上面的情况是中间确实会调用其他函数(先 Q(b) 再 Q(a))!因此还是需要先备份 callee-saved registers 到栈上,再传值,因此说免不了有 memory traffic;
那么什么时候不需要备份到栈上?
leave procedure / 另一个代码逻辑中,第一个寄存器在
P调用Q(b)前就被使用完了;Inter-Procedure Register Allocation:底层 ABI 支持 inter-procedure 的 calling conventions(例如允许多个过程调用共享一套寄存器);
Register Window(80 年代时,SPAC 引入此技术):
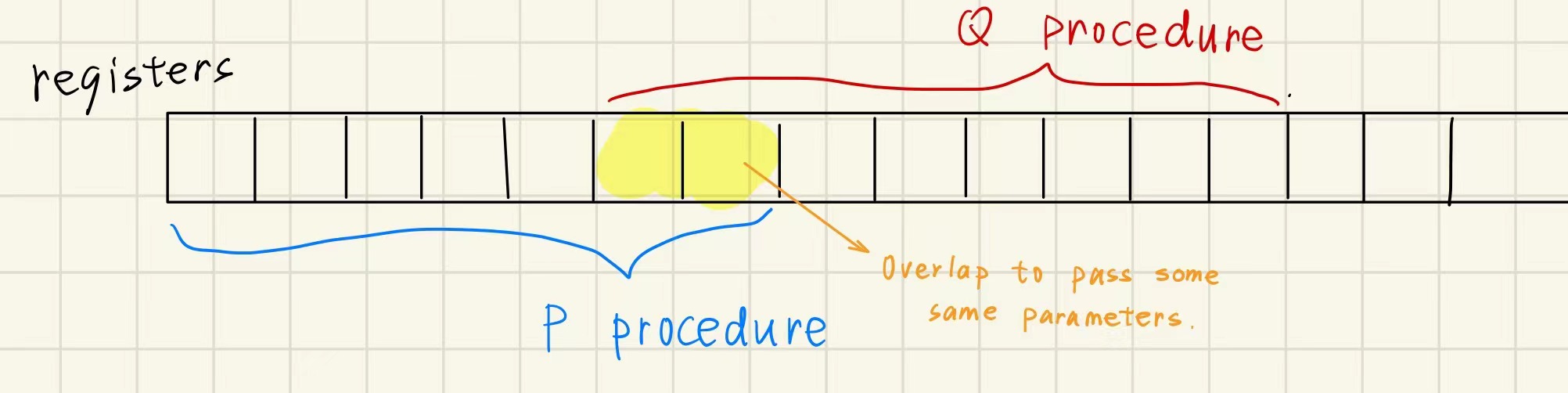
但是函数递归层数过多时,也会出现 memory traffic;
4.2.3 Variable-Length Argument List
在有些情况下,在 C/C++ 语言中,存在一种变长的函数参数调用方法,例如 printf。C/C++ 自身在实现这种签名不定的函数时,利用了 va_list/va_start/va_end 这类宏的定义,告诉编译器需要操作栈上的参数指针,由此实现不定长度参数传递。
于是我们发现,思路其实就是把参数当作列表放在栈上,然后由宏来获取这些列表的地址。例如:
xxxxxxxxxxvoid minprintf(char *fmt,...) { va_list ap; /* points to each unnamed arg in turn */ char *p,*sval; int ival; va_start(ap,fmt); /* make ap point to 1st unnamed arg */
for(p=fmt; *p; p++) { if(*p != '%') { putchar(*p); continue; } switch(*++p) { case 'd': ival = va_arg(ap,int); printf("%d",ival); break; case 's': for(sval = va_arg(ap,char *);*sval;sval++) putchar(*sval); break; default: putchar(*p); break; } // end switch } // end for va_end(ap); /* clean up when done */} // end function这也要求这些参数必须是左值、具有地址。如果可变长的参数里面有右值应该怎么办?
GCC 认为需要把放在寄存器中的参数值写到栈上,不过不是 caller 来写,caller 该按 registers 传就按 registers 传;只会在栈上分配一块空间,由 callee 在必要时写入栈上。
接下来我们讨论变量的 activation record 的问题。
4.2.4 Frame-resident Variables
变量只能放在栈上的原因无非以下几种:
函数使用引用传递这个变量;
某个过程需要访问该变量的地址;
嵌套函数要访问外层函数的局部变量(Python/Tiger/Javascript);
这个变量的大小过大,无法放在寄存器中;
前面的情况,我们需要保存 callee-saved registers,或者保存 caller 传来需要用的参数;
register spill(过多的局部变量和临时变量);
我们定义一个变量是 escaped 的,当且仅当:
变量通过函数引用传递;
变量的地址需要被获取;
嵌套函数需要访问外层的局部变量(在 Tiger Language 中,只有这种可能);
4.2.5 Global Variables
某些语言存在全局变量的概念。因为全局变量的生命周期并不在任何一个函数内,所以它的 activation record 自然不能放在栈上。
因此,这类变量会被编译器分配到固定的地址(称为 statically allocated),例如 .data / .rodata 的位置;
其中,对于 Tiger Language 而言,只有字符串常量会被作为 globals 分配在特定的位置。
4.2.6 Heap Variables
有些变量我们希望它们的生命周期不因为环境的析构而结束,而是希望手动 / GC 自动地回收它们,这类动态分配空间的变量就需要放在堆上。像 C/C++ 用 malloc 分配空间的变量就是 heap variables;
其中,对于 Tiger Language,records 和 array 需要存放在堆上,因为它们需要有无限增长的能力。
总结一下:
.textcode area 存放目标代码(对大多数语言来说大小固定、只读);.data静态数据区存放含有固定地址的变量(例如全局变量、静态变量等等,不包含代码);stack 包含当前活跃过程的 activation record,其中又包含了局部变量;
heap 包含了所有其他数据(动态分配的),在 tiger 中指 array 和 record;
stack 和 heap 都可以动态增长,前者向低地址,后者向高地址(注意判断不可 overlap);
4.3 Example for Tiger: Static Link
现在,我们着手解决一个问题,在 Tiger Language 中,如何实现对 escape variable 的解析?也就是说,如何让嵌套函数读到外层函数的局部变量?
我们知道,不同的局部变量一般放在不同栈帧(activation records) 中,想让嵌套子函数读到祖先函数的局部变量,就需要从前面的栈帧中找变量,这在很多语言中都是少见的行为。
注:比较常见的是在 GDB
bt指令调试时,或者libunwind库中就可以利用计算栈帧大小 / 利用程序段标记 /%ebp等等手段获得各个栈帧情况。
不过我们在编译阶段理论上就能知道一些在其他函数栈帧中的即将分配的变量情况(为上一层函数的局部变量事先计划在栈上准备一块空间),因此可以说编译器可以知道这些变量运行时的位置信息。
这样在内层函数使用这些 escape variables 时,直接将对应的 frame pointer 交给它来索引不就行了吗?这个做法就被称为 static link。
这也解释了为什么我们之前在看 tiger language layout 中,发现 static link 排在所有传递的参数前的原因了。其实就是把 上一层函数 的 frame pointer 传给 下一层函数,不过这个指针参数不会暴露给上层开发者,而是编译器使用这个 pointer 来查找 escape variables 罢了。
这也是为什么之前我们说 escape variables 必须放在栈上(frame-resident variables),而不能放在寄存器上;
还有一个问题,我们需要明确这些 escape variables 的偏移量,也就是说这些变量最好放在栈帧的固定位置上,方便从 static link 找到此层函数栈帧时能读到 escape variables。
Important
值得注意的是,static link 的内容和 caller/callee 的关系无关!因为它们的关系是动态的、相对地。
static link 采用的 frame pointer 指向,是根据函数在定义时的嵌套层数的关系来决定的。
例如有一个 tiger language:
xxxxxxxxxxtype tree = {key:string, left: tree, right: tree}
function prettyprint(tree: tree): string = let var output:= ""
function write(s:string) = output := concat(output, s)
function show(n:int, t:tree) = let function indent(s:string) = (for(i:=1 to n) do write(" "); output := concat(output,s);write(“\n”)) in if t=nil then indent(".") else (indent(t.key); show(n+1, t.left); show(n+1, t.right)) end
in show(0, tree); outputend各个函数的定义的嵌套层级是这样的:
xxxxxxxxxxmain 1prettyprint 2write 3show 3indent 4
因此传给 write 的 static link 应该是 prettyprint 的栈帧指针,而不是运行时 caller indent 的栈帧指针。
总结一下 static link 应该怎么生成。我们先设过程两个过程
当
此时必须要有
并且传给
当
indent访问output)、调用外层定义的函数(如上面的例子indent调用print),又或是同层级的调用(如上面例子show调自身)等等;此时有数学规律:从当前层数(
含义是,找到同时包裹(enclose)
为什么一定能在向上
因为
我们称上面的方法为 “follow-access-link”;
除了 follow-access-link,还有一种方法是 display 数组,d[i] 存放第 i 层最近活跃的栈帧的 frame pointer;当第 i 层最近有个新的函数被调用,则更新 d[i] 为这个被调用函数的栈帧,并将上一个 d[3] 旧值保存在 static link 中(保存的作用和 return address 很像,就是退出当前函数栈帧时恢复上一个 d[i]);
例如第 3 层的
show递归调用自身,则d[3]会从上一个show栈帧指向新的show栈帧;并将
d[3]旧值放在新函数栈帧的 static link 区域保存。
这样当我们调用 d[] 中可供查阅。这种方法的好处是比 follow-access-link 更快,坏处是需要额外的数据结构来记录。
比 display 更简单的方法是 lambda lifting,就是把
这种方法在现代语言中比较常见;
举个例子,比如在某种语言中:
xxxxxxxxxxdef f(x: int) -> int: def g(y: int) -> int: return x + 1 return g(0)可以使用 lambda lifting 构造一个匿名类:
xxxxxxxxxxclass __anonymous_g { x: int; y: int; constructor(x: int) { this.x = x; } g(y: int): int { return this.x + 1; }}这里的 __anonymous_g::g 实际上实现了上面 g 函数的效果。
4.4 Language Frame & Escape Analysis
我们知道,在一个语言中,不同的函数虽然运行时数据各不相同,但由于 calling conventions 的存在,我们可以在编译时,就排布出相对固定的函数栈帧的结构,就像前面提到的 Tiger 的栈帧:

所有传递的函数参数存放位置;
需要实现 “view-shift” 的指令(后面讨论);
目前已经分配的局部变量的数量和位置(编译器管理
%rsp);函数在机器代码的开始位置(记忆 label 或 return address);
这些信息都需要在编译期间预先管理栈时需要知道的。
例如我们在分析到一个 Function Definition 时,希望为一类新的函数创建一个栈空间(为什么是新的函数,回想汇编中一个函数定义的位置是唯一的):
xxxxxxxxxx/** * @param name 函数 Label 名称 * @param formals 函数中表示哪些参数是 escape variable 的 bool 数组 */frame::Frame NewFrame(temp::Label *name, std::list<bool> formals);例如遇到一个 func f(arg1, arg2, arg3) 的定义时,可以为它创建一个栈帧的模板:NewFrame(f, {true, false, false});
不过它的具体实现已经开始取决于 target machine 的架构了。因为不同的架构(x86 还是 ARM/RISC-V)的 calling conventions 是不同的。
对于不同的架构,我们一般实现不同的 Frame,此时还会用到另一个类 Access 来表征对数据的访问情况:
xxxxxxxxxxnamespace frame { class Access { public: virtual llvm::Value *ToLLVMVal(llvm::Value *frame_addr_ptr) const = 0; }; class InRegAccess : public Access; class InFrameAccess : public Access { public: int offset; // 对于 escape variable,其 offset(针对当前栈帧)需要是固定值 frame::Frame *parent_frame; // 这个 variable 所在的栈帧
explicit InFrameAccess(int offset, frame::Frame *parent) : offset(offset), parent_frame(parent) {}
llvm::Value *ToLLVMVal(llvm::Value *frame_addr_addr) const override; };}我们可以在 Access 中描述一个函数哪些变量分配在寄存器中,哪些变量分配在栈上,方便后续的翻译工作。
有了现在对于变量管理的定义(frame::Access,包括了变量所处栈帧、相对栈帧的位置等信息),现在我们需要根据前面提到的 “对栈帧信息的需求” 设计 Frame 的接口:
xxxxxxxxxxclass Frame { public: /* other members and methods */ std::list<frame::Access *> *formals_; // 此成员就能清楚地描述函数栈帧的参数存放的位置};现在我们描述好了栈帧上的函数参数,暂时把视角转移到另一个机制:“shift of view”;
我们知道,caller 和 callee 对于参数的看法是不同的。我们讨论统一的情况:以 IA-32(x86)为例,所有参数都在栈上传递(因为 x86-64 有一部分在寄存器上,不方便说明)。这个时候 caller 就是在向栈顶推数据,而 callee 需要将 %rsp 加上一些值够到上一层函数的栈帧中取数据。
编译器为了方便管理这种约定,抽象出了 shift-of-view 的机制,在 caller 传递参数后,转到 callee 的视角来看如何读出这些参数。
以 IA-32 为例,如何实现 shift-of-view?假设一个函数有 3 个栈上参数 InFrameAccess(8)、InFrameAccess(12)、InFrameAccess(16),这个传入的 “8、12、16” 的 offset 就是站在 caller 栈帧视角来看的。如果编译器需要为 callee 读取这些参数,就需要在 callee 中生成这些汇编代码:
xxxxxxxxxxpushl %ebpmovl %esp, %ebpsubl $K, %esp在 x86-64 中,有部分参数可以放在寄存器中,有一部分 escape variables 和 register spill variables 就放在栈上。假设函数有参数 InFrameAccess(0)、InRegAccess(T157)、InRegAccess(T158)(T-157 和 T-158 表示的是寄存器分配编号,先抽象成无限寄存器,后面在 “寄存器分配” 阶段再考虑物理寄存器的事);
如果在 callee 中,我们还是先根据 callee 中的 %esp 计算出在 caller 中表示的栈上参数的位置:
xxxxxxxxxx%rsp <- %rsp - KM[%rsp+K] <- %rdit157 <- %rsit158 <- %rdx
接下来,我们继续添加 Frame 的接口,让编译器管理局部变量:
xxxxxxxxxxclass Frame { public: /* other members and methods */ std::list<frame::Access *> *formals_; // 此成员就能清楚地描述函数栈帧的参数存放的位置 frame::Access *AllocLocal(); // 在栈上预留局部变量的位置,方便代码生成和栈帧管理};最后函数栈的总体大小就由这些 local variables 的数量、参数情况等等来决定。
值得注意的是,有个潜在优化的点:如果后面发现两个 frame-resident variables 可以共用一块栈上的空间,可以通过分析分析变量生命周期来进行进一步压缩。例如下面的 a 和 b;
xxxxxxxxxxint test() { int a = 0; printf("%p", &a); // a 的生命周期结束 int b = 0; printf("%p", &b);}需要注意的是,在不同的 scope(nested block)中,即便是同名的变量也要考虑分配单独的 slot,例如:
xxxxxxxxxxlet var x=5 in let var x = "abc" in x endend
最后我们以 Tiger Language 为例,看看如何描述和管理 escape variables:
xxxxxxxxxxnamespace esc { void EscFinder::FindEscape(); using EscEnvPtr = sym::Table<esc::EscapeEntry> *; // 存放以 escape variables 为结点的列表 // 向管理 escape variables 的列表中插入当前 escape variable 的信息 // 由于这个函数在每个 VarDec 时执行,那时还不清除该变量是否会逃逸,因此存放 escape_ 字段的指针 EscapeEntry(int d /* depth */, bool *escaped);}然后在一轮 semantic analysis 后,再来一轮 traverse(也可和 type checking 一起进行),看看每个在 EscEnvPtr 管理的列表中的变量是否有在 depth > d 的地方用到过,如果用到,说明是 escaped variable,则先找它所在的 environment,再把它的 escape_ 字段改为 TRUE;
然后实现 Traverse,和 Semantic Analysis 的过程相似:
xxxxxxxxxxnamespace absyn { void Exp::Traverse(esc::EscEnvPtr env, int depth); void Dec::Traverse(esc::EscEnvPtr env, int depth); void Var::Traverse(esc::EscEnvPtr env, int depth);}
注意为了实现 Translation,以及上面提到的 escape analysis,封装了一些接口:
xxxxxxxxxxnamespace tr { // 定义了栈帧对应的嵌套层数 class Level { public: frame::Frame *frame_; Level *parent_; }; // 在变量管理 frame::Access 的基础上 // 加入了当前栈帧的层数一起封装 class Access { public: Level *level_; frame::Access *access_; Access(Level *level, frame::Access *access) : level_(level), access_(access){} static Access *AllocLocal(Level *level, bool escape); }; } // namespace tr这样在 Value/Type Environment 中添加这些对象,如 VarEntry:
xxxxxxxxxxclass VarEntry: public EnvEntry {public: tr::Access *access_; type::Ty *ty_; VarEntry(tr::Access *access, type::Ty *ty, bool readonly = false);};然后在 Translation 过程中,我们:
函数体内
tr::Level::NewLevel()管理层级(FunctionDec::Translate);变量声明时向分配一块局部变量的空间(是否在栈上待定)
tr::Access::AllocLocal(level, escape_),并把这个tr::Access返回值存储在VarEntry中等待生成代码时使用;
在 Tiger 中,由于 Frame 并不知道 static link 的信息,因此在 translate 的遍历过程中将 static link 作为隐藏的第一参数传进去(就像之前的 Tiger 栈帧图描述的);
因此 tr::Level::NewLevel() 的接口:
xxxxxxxxxxclass Level { public: frame::Frame *frame_; Level *parent_; Level *NewLevel(tr::Level parent, temp::Label label, std::list<bool> formals) { formals.push_front(true); NewFrame(label, formals); // ... }};指定一个特定的 Level(main_level),其中包裹了所有库函数:
xxxxxxxxxxtr::ProgTr { Level *main_level_; }在 Semantic Analysis 后,我们需要将这个值事先传递给 Translation 过程。
4.5 Introduction to LLVM IR
4.5.1 Basic Concepts
现在针对 Translation 的几乎所有准备工作都介绍完毕了,我们现在了解一下 Translation 需要翻译成什么:IR(Intermediate Representation)Tree;
为了通用性,我们主要讨论 LLVM 规范定义的 IR 树的结构,学习如何生成 LLVM IR 的格式(这样能利用 LLVM Back-end,很快地把我们之前学习的内容用起来)。
什么是 LLVM?它和 GCC Toolkits 并列,但模块性更好。
LLVM(Low-Level Virtual Machine)是构架编译器 (compiler) 的框架系统,以 C++ 编写而成,用于优化以任意程序语言编写的程序的编译时间 (compile-time)、链接时间 (link-time)、运行时间 (run-time) 以及空闲时间 (idle-time),对开发者保持开放,并兼容已有脚本。
它的社区比较庞大,因此无论对前端语言优化,还是对底层特定架构的优化都做的不逊色于 GCC;
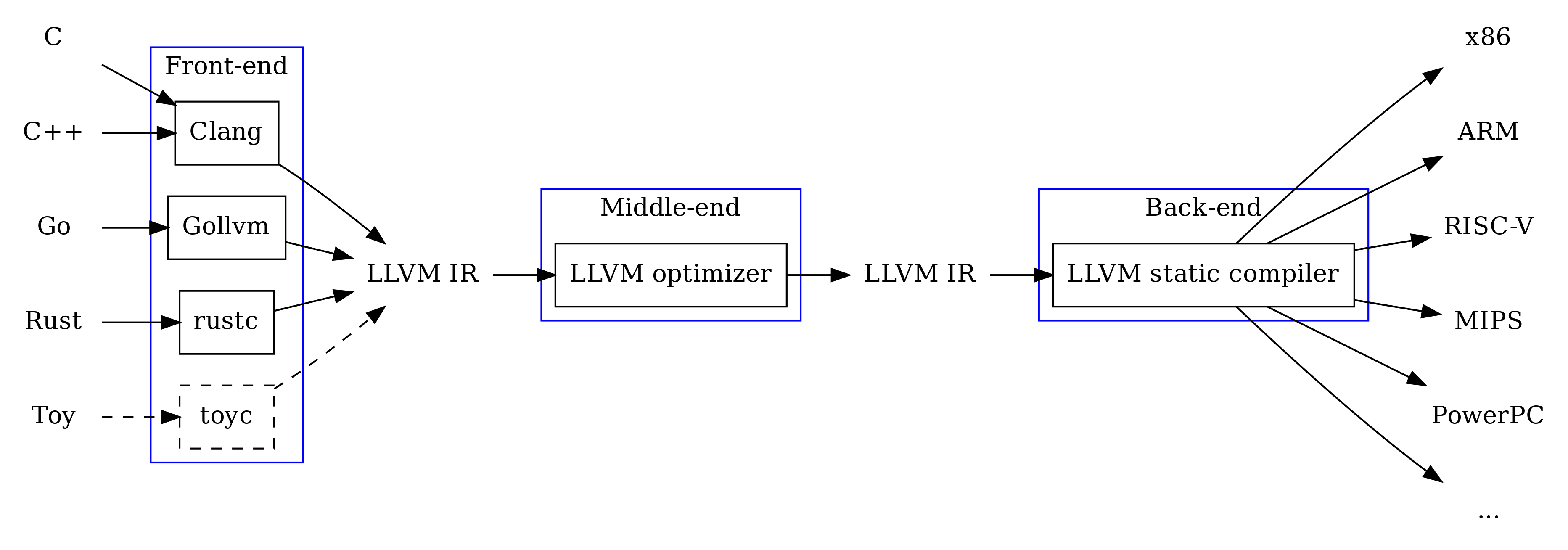
例如在 Rust 语言中,可以使用
cargo将参数传给rustc以生成项目的 LLVM IR 表示:xxxxxxxxxx# cargo [++toolchain] [OPTIONS]cargo rustc -- --emit=llvm-ir
现在举个 LLVM IR Tree 的例子:
一个 C 语言程序:
xxxxxxxxxxint calculate_and_compare(int a, int b, int c) { int sum = a + b; if (sum > c) { return sum; } else { return c; }}经过 LLVM 前端转换后,LLVM IR Tree 如下所示:
xxxxxxxxxxdefine i32 @calculate_and_compare(i32 %a, i32 %b, i32 %c) {entry: %sum = add i32 %a, %b %cmp = icmp sgt i32 %sum, %c br i1 %cmp, label %return_a, label %return_breturn_a: ret i32 %sumreturn_b: ret i32 %c}注意到一些语法:
LLVM IR Tree 中可以指定任意多的局部或全局变量(Pattern:
%xxx);在 LLVM IR 中有 “无限多虚拟寄存器” 的假设。后面在寄存器分配阶段时再考虑有限的问题(映射)。
LLVM IR Tree 中,类型表示方法:
i1 / i16 / i32(integer 1/16/32 bits);还有很多其他类型,我们后面讨论。
大多数 LLVM IR 中的操作符都是 3 元操作符(类似 RISC-V 汇编的优秀设计):
add <type> <var1> <var2> -> <ans>:还有很多语法,我们在讨论 LLVM IR Builder 时讨论;
LLVM IR 使用 Label + Jump(
br指令)的方法进行跳转,从而支持循环和分支控制流。尤其是重要跳转指令:
br <type> <var>, label %<then-labelname>, label %<else-labelname>;LLVM IR 定义函数的方法比较简单:
xxxxxxxxxxdefine i32 @calculate_and_compare(i32 %a, i32 %b, i32 %c) {# ...ret i32 %sum}
LLVM 中还有一些概念:
Basic Blocks:从某个 Label 开始,终结于一次
br(分支跳转)指令或者ret;在大量实践中可以知道,使用 Basic Block 作为分析/优化的基本单元是非常合适的;
Value:在 LLVM IR 中,大多数语法结点都是一类抽象概念 Value 的子结点。
Virtual Register、Actual Parameters(实参)、Label、Basic Block 都可以看作一个 LLVM Value;
Local Value 都以
%开头,Global Value 都以@开头;
Register Assignment:在 LLVM 中,规定禁止了对 Value 的覆写(二次修改)行为,这里借鉴了 Rust 所有权的思想,主要有两点好处:
数据流分析(留出了清晰、可预测的数据流)、方便程序优化;
给寄存器分配阶段留下改进空间;
这被称为 “Static Single-Assignment form”(SSA);
例如 C 程序:
xxxxxxxxxxint sum = a + b;sum = sum + c;只能这么转换:
xxxxxxxxxx%sum = add i32 %a, %b# 错误:%sum = add i32 %sum, %c# 正确:%sum1 = add i32 %sum, %c
4.5.2 LLVM IR Builder
Overview
如何将 AST 转为 IR Tree?LLVM 中提供了一个工具:LLVM IR Builder。它的作用是通过代码方法规定了将 AST 转换为 IR Tree 的规则。
如果准备构建这样的 IR Tree:
xxxxxxxxxxentry: %sum = add i32 %a, %b %sum = add i32 %sum, %c %sum1 = add i32 %sum, %cLLVM IR Builder 的代码示例如下:
xxxxxxxxxx// 创建一个 LLVM IR Builder// 同时开始管理全局上下文(管理全局配置、状态、类型等等)// module 表示一个编译单元LLVMContext Context;Module *M = new Module("my_module", Context);IRBuilder<> Builder(Context);
// 创建一个在 IR 上的函数FunctionType *FuncType = FunctionType::get(… …Function *Func = Function::Create(FuncType … … auto ArgIt = Func->arg_begin();Value *a = ArgIt++;Value *b = ArgIt++;
// 创建一条指令// %sum = add i32 %a, %bBasicBlock *EntryBB = BasicBlock::Create(Context, "entry", Func);Builder.SetInsertPoint(EntryBB);Value *sum = Builder.CreateAdd(a, b, "sum");先过一遍,后面介绍详细内容。
Type System in LLVM IR & Its Builder
而在 LLVM IR Builder 中,我们就需要认识 IR 的类型系统:
整型:
i1, i8, i16, i32, i64,前面已经见过了,需要获取类型指针:xxxxxxxxxx// LLVM IR Builderllvm::Type *i32Ty = llvm::Type::getInt32Ty(context);浮点型:
float, double:xxxxxxxxxx// LLVM IR Builderllvm::Type *floatTy = llvm::Type::getFloatTy(context);指针型:
i32*, i64*, ...;xxxxxxxxxx// LLVM IR Builder// 其中第二参数表示 address space,0 代表 globalllvm::PointerType::get(i32Ty, 0);结构体型:这里需要类型定义:
xxxxxxxxxx# LLVM IR Syntax%mystruct = type {i32, float}注意类型定义不是 LLVM Value!
xxxxxxxxxx// LLVM IR Builderllvm::StructType::create(context, {i32Ty, floatTy}, "mystruct");数组类型:LLVM 提供了定长数组的定义:
xxxxxxxxxx# LLVM IR Syntax[10 x i32][20 x %mystruct]xxxxxxxxxx// LLVM IR Builderllvm::ArrayType::get(i32Ty, 10);注:动态长度数组应该创建在堆上,由指针型管理。
函数类型:和结构体型一样,也是 IR 的类型定义语法:
xxxxxxxxxx# LLVM IR Syntax# 依次是返回值类型、顺序参数类型%my_function_type = type i32 (i32, i32)xxxxxxxxxx// LLVM IR Builder// 最后一个参数是 isVarArgs,表示这个函数是否是可变长参数列表(例如 C 中的 printf 就是)llvm::FunctionType::get(i32Ty, {i32Ty, i32Ty}, false);
Local Variable Management of LLVM IR
在 LLVM IR 中,有局部变量的分配的方法:
栈上分配:stack allocation using
alloca;寄存器分配:virtual registers;
对同一个 C 语句:int sum = a + b;,
栈上分配的方法:
xxxxxxxxxx# LLVM IR Syntax%sum_ptr = alloca i32%a_val = load i32, i32* %a_ptr%b_val = load i32, i32* %b_ptr%sum_val = add i32 %a_val, %b_valstore i32 %sum_val i32* %sum_ptr其中
alloca表示要在 stack 上分配一个空间,它会返回计划的相对当前栈帧的变量偏移量(offset),而不需要手动指定要移动%rsp这样的寄存器。
寄存器分配的方法:
xxxxxxxxxx%sum = add i32 %a, %b寄存器分配方法看起来这种方法很简单,实际上由于 SSA 的限制,同名的变量实际上会被分配不同的 virtual register,数据流的实际处理会比较复杂。
尤其是这种情况:
xxxxxxxxxxint sum;if (a) { sum = b + 1;}else { sum = b + 2; sum = sum + c;}我们要生成 IR Tree:
xxxxxxxxxxentry: br i1 %a, label %true, label %falsetrue: %sum1 = add i32 %b, 1 br label %nextfalse: %sum2 = add i32 %b, 2 br label %nextnext: # 怎么做??? %sum3 = add i32 %???, %c由于 SSA,导致我们的 add 操作不清楚应该找哪个 Virtual Register 了!
这时就引入 IR Tree 的另一个重要指令:phi(虚拟寄存器合并指令),将不同的 register value 从不同的 Basic Blocks 中合并起来:
xxxxxxxxxxentry: br i1 %a, label %true, label %falsetrue: %sum1 = add i32 %b, 1 br label %endfalse: %sum2 = add i32 %b, 2 br label %endnext: # phi <type> [<val1>, %<labelname1>], [<val2>, %<labelname2>] %sum3 = phi i32 [%sum1, %true], [%sum2, %false] %sum4 = add i32 %sum3, %c
不过总结一下,将变量只分配在寄存器上,是属于一种可选的优化方法。多数的 LLVM-based Compiler(如 Clang)在不优化的情况下,都是将变量直接分配在栈上的。
在 Tiger Language 中,情况有些不一样。因为 Tiger 的栈帧布局和 C/C++ 的有些区别:多了一个 static link 作为固定参数。
也就是说,我们需要自己管理一个新的变量 %my_sp 来计算栈上的 static link entry 以及其他变量的位置。举个例子:
xxxxxxxxxxint sum;sum = 27;以栈上管理的方式会被转为 InFrameAccess(offset = 8),最终位于当前栈帧的底部。如果我们管理的 %my_sp 位于当前栈顶,那么需要以下步骤:
xxxxxxxxxx%1 = add i64 %my_sp, %framesize%2 = add i64, %1, -8# Type Convertion%3 = inttoptr i64 %2 to i32*store i32 27, i32* %3, align 4
Global Variables Management of LLVM IR
LLVM IR 规定 global variables 可以不定义在任何函数体内,示例:
xxxxxxxxxx# LLVM IR Syntax@myGlobalVar = global i32 42# Constant 前缀@main_framesize_global = constant i64 40# 全局常量字符串@myString = private unnamed_addr constant [14 x i8] c"Hello, LLVM!\00"
需要注意的是,所有 global variables 默认都需要以指针操作,例如:
xxxxxxxxxxentry: %main_framesize = load i64, i64* @main_framesize_global, align 4
LLVM IR Instructions
下面介绍 LLVM IR Tree 中的常见指令:
四则运算:
add/sub/mul/sdiv <type> <var1> <var2> -> <ans>;对应的 LLVM IR Builder 指令如下:xxxxxxxxxx// 创建 LLVM Valuellvm::Value *result1 = ir_builder->CreateAdd(a, b, "result1");llvm::Value *result2 = ir_builder->CreateSub(a, b, "result2");llvm::Value *result3 = ir_builder->CreateMul(a, b, "result3");llvm::Value *result4 = ir_builder->CreateSDiv(a, b, "result4");逻辑运算:
and/or <type> <var1> <var2> -> <ans>;比较运算:
icmp <op> <type> <var1> <var2> -> i1;其中
<op>运算符可以是:eq, ne, sl, sg, sle, sge(s前缀表示 signed);栈空间分配管理:
alloca <type> -> <ptrVar>;访存操作:
load <type>, <ptrTy> <ptrVar> -> <var>;store <type> <var>, <ptrTy> <ptrVar>;
类型转换:
trunc/zext/sext <type> <var> to <newTy> -> <var>;分别对应截断(大数据类型向小的转换)、零扩展、符号扩展;
指针和值间相互转换:
inttoptr <intTy> <var> to <ptrTy> -> <ptrVar>;ptrtoint <ptrTy> <ptrVar> to <newTy> -> <var>;指针间相互转换:例如
%new_ptr = bitcast %type1* %old_ptr to %type2*;
计算子元素地址(类似 x86 中的
lea指令):xxxxxxxxxx%elem_ptr = getelementptr %StructTy, %StructTy* %base_ptr, i32 %idx1, i32 %idx2[, ...]如对于下面的结构体和函数定义:
xxxxxxxxxxstruct my_struct {int f1;int f2;};void munge(struct my_struct *base) {base[0].f1 = base[1].f1 + base[2].f2;}xxxxxxxxxx# LLVM IR Syntax%my_struct = type {i32 i32}define void @munge(%my_struct* %base) {entry:# 注意 base[1].f1 的内存地址被翻译成 idx1 = 1, idx2 = 0 (f1 是 struct 中第 0 个 i32 数据块)%tmp = getelementptr %my_struct, %my_struct* %base, i32 1, i32 0%tmp1 = load i32, i32* %tmp%tmp2 = getelementptr % my_struct, %my_struct* %base, i32 2, i32 1%tmp3 = load i32, i32* %tmp2%tmp4 = add i32 %tmp3, %tmp1%tmp5 = getelementptr % my_struct, %my_struct* %base, i32 0, i32 0store i32 %tmp4, i32* %tmp5ret void}跳转:
无条件跳转:
br label %<labelname>;有条件跳转:
br i1 <cond>, label %<then-labelname>, label %<else-labelname>;
函数调用:
call <type> @<func_name>(<type1> %<name1>[, ...]);ret <type> <var>(如果是 procedure,则ret void);
寄存器合并:需要确保枚举了所有可能的组合;
phi <type> <var1>, %<labelname1>[, <var2>, %<labelname2>, ...];对应的 LLVM IR Builder 写法:xxxxxxxxxxllvm::PHINode *result = ir_builder->CreatePHI(ir_builder->getInt32Ty(), 2);result->addIncoming(val1, true_bb);result->addIncoming(val2, false_bb);
How to Write A LLVM IR Builder From Scratch?
之前的内容,都是从 IR Tree 语法的角度切入介绍 IR Tree 的结构,但是大家没法直观了解如何编写 LLVM IR Builder。那么这节就主要讨论从 LLVM IR Builder 出发,如何写一个 Builder,为之后的 Translation 生成 LLVM IR Tree 打下理论基础。
4.6 In-Frame Variable Management
最后在实现前再考虑一个问题,我们之前介绍了,如果我们将所有变量都作为 InFrameAccess,然后利用 LLVM IR 的 alloca 指令分配栈帧,那么相当于 offset、frame size 的大小都是黑盒,LLVM 后端帮你完成了。
但是,我们如果想要实现前面章节提到的 escape variables,那么我们就没法得到这些信息(variable offset 等等)来填充 static-link(因为 LLVM 的设计更多考虑的是 C 的特性)!
因此我们在 IR Builder 中就手动来管理 %rsp 栈指针。我们不仅向每个函数传入默认的 static link 做第一参数,而且做如下动作来取出某个偏移量的外部变量:
xxxxxxxxxxdefine void @test(i64 %par_sp, i64 %par_sl) {entry: # ... %test_sp = sub i64 %par_sp, %test_framesize # 移动到当前栈帧应该在位置 %x_offset = add i64 %test_framesize, -8 # 计算外部变量在外部栈帧中的偏移量(从栈顶向底看) %x_addr = add i64 %test_sp, %x_offset # 将 x_addr 偏移到需要的外部变量的地址 %x_ptr = inttoptr i64 %x_addr to i32* # 成功获取了外部变量的内存地址!实现了 store i32 1, i32* %x_ptr, align 4 # escape variable 从 static link 上读取 ret void} define i32 @main(i64 %par_sp) {entry: # ... call void @test(%sp, %sl)}
4.7 Translation Implementation: To LLVM IR
4.7.1 Definitions
有了前面的准备,现在我们正式讨论 Translation 的任务。
如何将 AST 转成 LLVM IR?
以 tr::ValAndTy *SimpleVar::Translate(...) 为例。假设这个变量是 InFrame 的,并且位于在 level(栈帧对应的嵌套层数类型的实例)中。
因此我们需要实现这个 IR:
xxxxxxxxxx%x_offset = add i64 %func_framesize, -k%x_addr = add i64 %func_sp, %x_offset %x_ptr = inttoptr i64 %x_addr to i32*因此可以用 IR Builder 这么表示:
xxxxxxxxxxllvm::Value *val = ir_builder->CreateIntToPtr( var_faccess->ToLLVMVal(level->get_sp()), llvm::PointerType::get(var_entry->ty_->GetLLVMType(), 0), "x_ptr");return new tr::ValAndTy(val, var_entry->ty_->ActualTy());如果加载 static link?我们可以通过下面的方法实现:
xxxxxxxxxxllvm::Value *val = level->get_sp();while (level != var_level) { // The first accessible frame-offset_ values is the static link auto sl_formal = level->Formals()->begin(); llvm::Value *static_link_addr = (*sl_formal)->access_->ToLLVMVal(val); llvm::Value *static_link_ptr = ir_builder->CreateIntToPtr( static_link_addr, llvm::Type::getInt64PtrTy(ir_builder->getContext())); val = ir_builder->CreateLoad(ir_builder->getInt64Ty(), static_link_ptr); level = level->parent_;}// After N loops, access actual var, get an address (can be turn into a pointer later)val = var_faccess->ToLLVMVal(val);
4.7.2 An Example for Tiger Language
如何处理数组、结构体?
在 Pascal 中,一个数组变量直接意味着整个 array 的内容(相当于 C++ 的 std::vector),使用赋值运算会将其中的值完整复制;
在 C 中,一个数组变量(注意定义方法是 int a[] 而不是 int *a)意味着一个常量指针,不允许对数组变量再次赋值;
而在 Java、ML、Tiger 中,一个数组变量不是指针,但底层和指针类似。
例如在 Tiger 中,一个数组名不是指针常量,例如 var a := intArray[12] of 0(已经定义 type intArray = array of int)的 a 就是创建了 12 个 integer 连续空间,并且把 a 的值设置为空间起点地址。
Tiger 的结构体(record)也是指针。
左值 和 右值?
一般来说,左值和右值相比不仅可以作为 expression,更重要的含义是它能代表一个 “内存地址”(能够存储右值)。
左值中有一类比较特殊:structured l-value(在 C 中就是结构体,在 Pascal 中就是 Array),它代表了一组有内存地址的左值,所有成员变量都意味着地址。
所以在赋值过程中,structured l-value 在复制构造的过程中需要考虑是否进行 memory copy(尤其是没有指针的语言的实现)。
但在 Tiger 中,没有 structured l-value,数组和结构体之类的变量就是这段变量的内存地址,然后访问内部元素/成员时(例如 a[i])总是先找 a 的内存地址 p,然后对 p 的地址进行计算进而取值。
我们以 SubscriptVar(取下标变量)的翻译为例。我们为了配合 LLVM 的类型系统,把每个变量都视为指针:
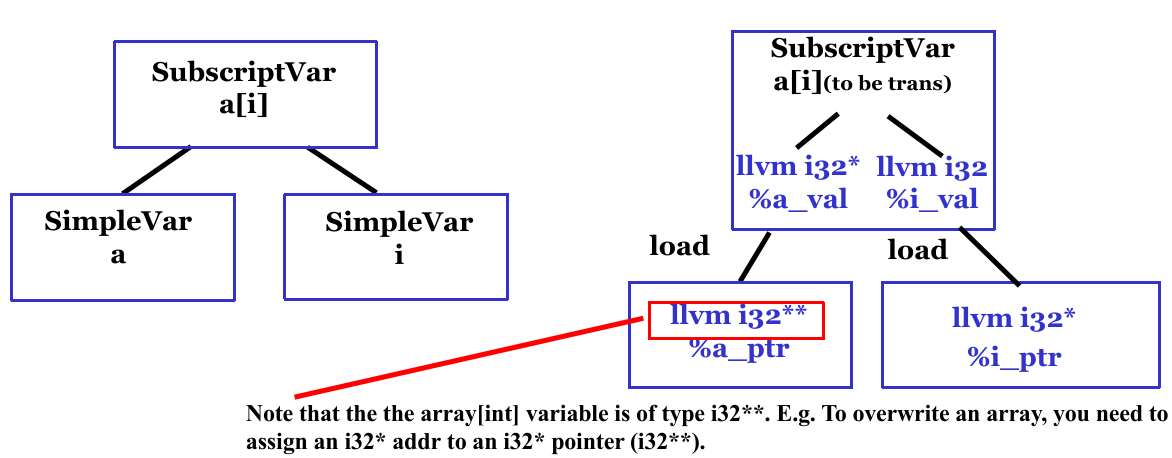
最终会被翻译成 LLVM 的 GEP 指令:
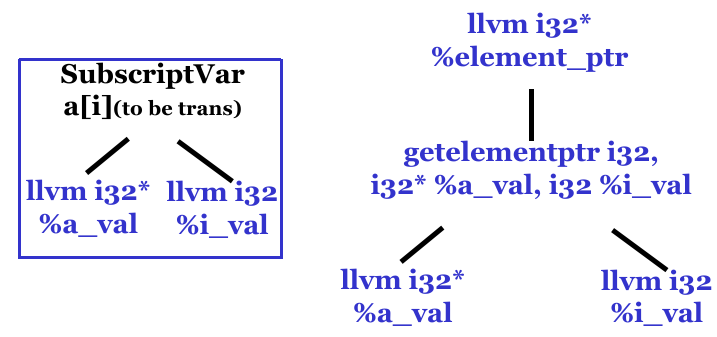
另外,对于一个结构体 a.f 的解析:
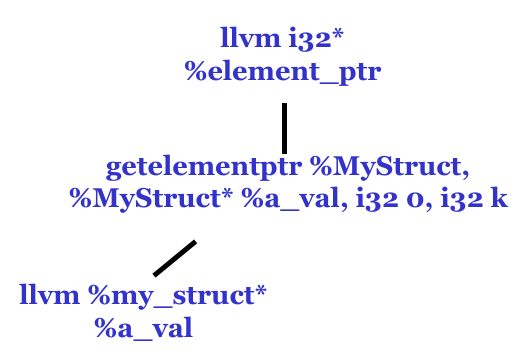
总而言之,注意当数组本身被赋值时,a = b,则 a 的类型是 int**;如果是取数组中的某个元素,则又可以中途 load 为 int*。然后结构体是同理的。
4.7.3 Memory Safety
Array Bound Check:耗时,通常需要结合优化方案;
Null Check;
4.7.4 Translate Arithmetic
Tiger 中直接不支持浮点数,因此只需要关注 type conversion (例如指针和数字的加法)就行。
4.7.5 Translate Conditionals
如何翻译分支语句?以 if e1 then e2 else e3 为例:
首先,我们需要为 e1 创建 Basic Block(test_bb),然后 IR Builder 直接跳过去。生成 test_bb 的代码后,把判断结果作为 flag 来决定跳到不同的 basic block 中(最好用 icmp 不要强转):
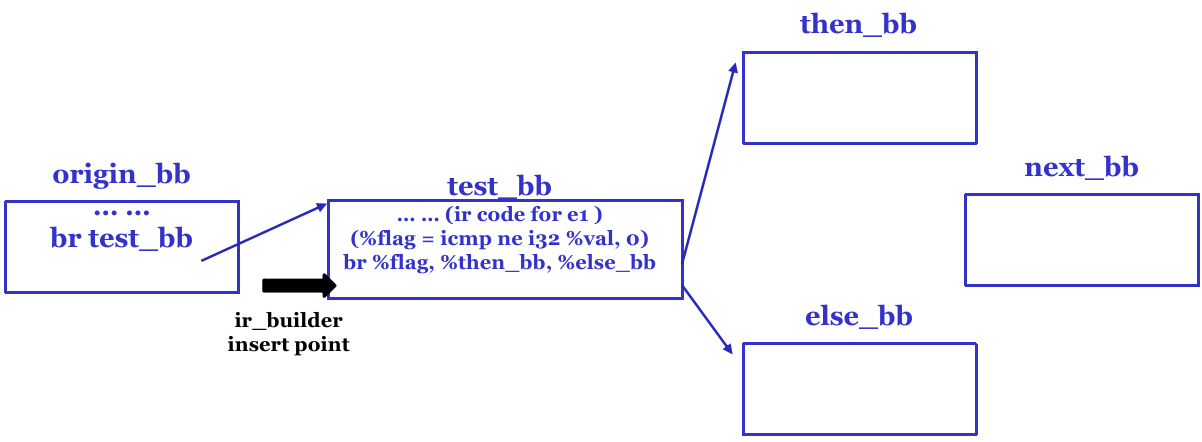
然后分别生成 then_bb 和 else_bb 的代码:
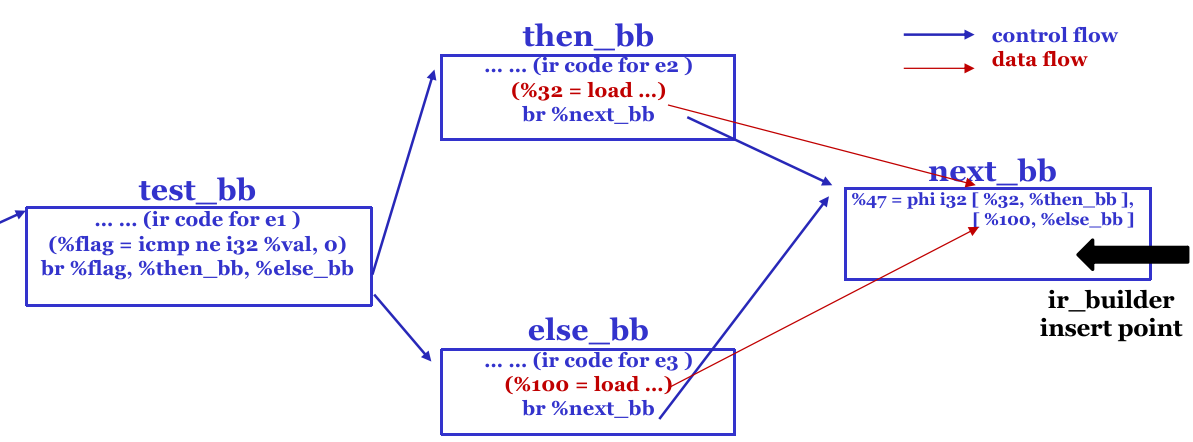
看起来最后直接生成 br %next_bb,然后在 next_bb 中生成 phi 指令的 label 直接用前两个(对吗?)basic blocks 的 label,然后注意两个点:
如果
then_bb/else_bb的后面已经有br指令,则无需再添加;如果
then_bb和else_bb的返回类型不相同,注意进行 type conversion;
是不是就行了?可惜并不是 “前两个”,考虑下面的嵌套情况:
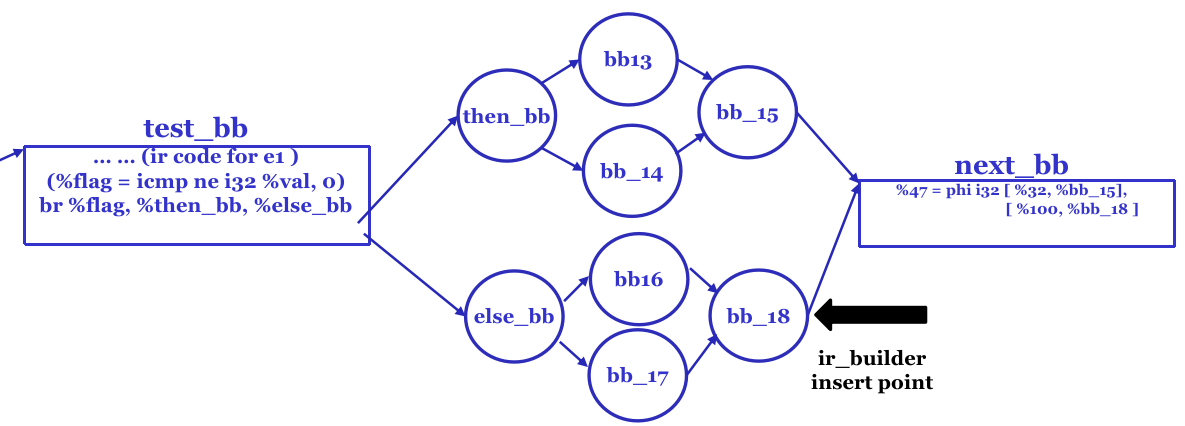
因此我们不是要找 “前两个” basic blocks,而是 “最近两个活跃的” basic blocks。这个需求已经由 LLVM 帮我们实现了,可以直接使用 llvm::IRBuilderBase::GetInsertBlock() 来获得最近两次活跃的 bb_15 和 bb_18;
4.7.6 Translate Logical Expression
对大多数逻辑表达式而言(主要是比较运算),翻译是很简单的,直接使用 LLVM 提供的 IR 指令 icmp 就行;而 String Comparison 则可以使用运行时的 stringEqual 函数即可解决问题。
主要的难点在于 AND 和 OR 逻辑短路运算。我们可以这么设计(以 OR 为例):
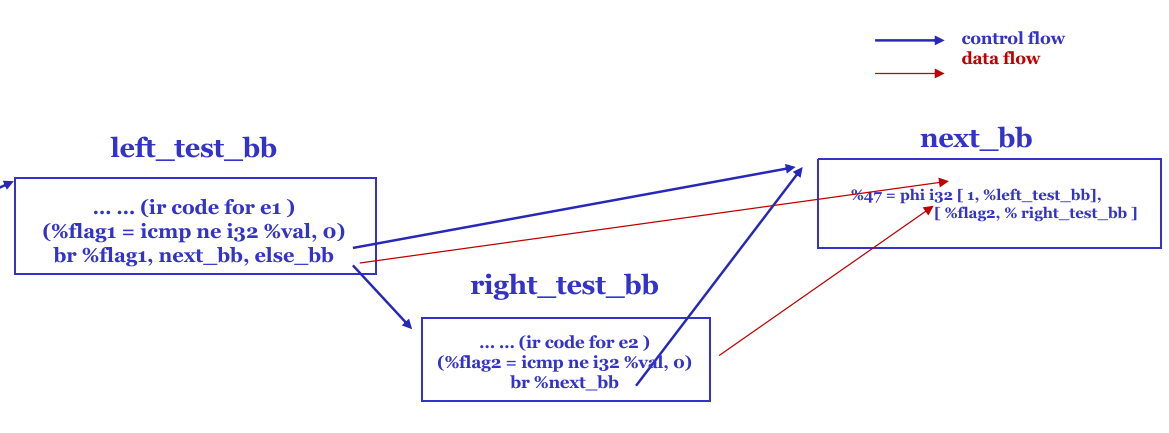
4.7.7 String Creation
在 Tiger 语言中,String 是在固定地址的连续内存空间,并且它的各个字符被初始化为指定的值。在 Tiger 中这么处理:
前面一个字存放字符串长度,后面一个字存放字符串指针(整体数据结构固定长度);
xxxxxxxxxxstruct LLVMString {int length; // length of stringchar padding[4]; // padding for alignmentchar *chars; // actual string content};因此在 LLVM IR 中表示成两个变量:
xxxxxxxxxx%string = type { i32, i8* }@0 = private unnamed_addr constant [21 x i8]c"hey! Bigger than 3!\0A\00", align 1@str = constant %string { i32 20, i8*getelementptr inbounds ([21 x i8], [21 x i8]* @0, i32 0, i32 0) }我们可以通过 LLVM IR Builder 接口
type::StrngTy::CreateGloablStringStructPtr(std::string str)来自动构造上述 IR;所有关于字符串的函数都由 runtime system 提供;
这些函数如果需要返回字符串,则从 heap 分配;
4.7.8 Record & Array Creation
对 Simple Variable 而言,我们直接将值分配在栈上;
而对于简单的结构体初始化语句 {f1: a1, f2: a2, ..., fn: an},则必须分配在堆中(不能在栈上),因为这些数据结构可以在 procedure 结束后继续使用。
我们分配的方法是调用语言的外部 memory-allocation function:
创建共 n 字的空间(因为每个数据域最大 1 字,要么是整型、要么是数组/结构体指针);
返回一个可以转成指针的
i64;
然后使用多次 GEP 和 store 来按用户指定的信息初始化这个结构体。
最终返回的结果就是之前分配的内存地址起始空间;
数组的创建和结构体的创建很类似。
和字符串比较函数一样,创建数组的函数同样使用 runtime-system function init_array(n, b) 来完成。其目标是:
创建一个 N 字空间(同样,一个数组的元素大小最多 1 字,整型、结构体/数组指针);
按照用户的指示初始化所有元素;
返回一个
i64,可以转换成指针;
值得注意的是,如果要被赋值的 b 又是一个数组/结构体,创建起来还是比较麻烦的。初始化元素的方法有两种:
为每个元素创建一个独立的数组/结构体对象;
让每个元素指向同一个数组/结构体对象;
如何在 IR Builder 中实现?我们可以通过创建 runtime-system function 的方法来完成:
xxxxxxxxxx// 定义时llvm::FunctionType *init_array_func_type = llvm::FunctionType::get( ir_builder->getInt64Ty(), {ir_builder->getInt32Ty(), ir_builder->getInt64Ty()}, false);llvm::Function *init_array = llvm::Function::Create(init_array_func_type, llvm::Function::ExternalLinkage, "init_array", ir_module);// ...
// 创建时llvm::Value *array_addr = ir_builder->CreateCall(init_array,{len_val, init_val});这样就创建了一个 init_array(N, b) 的语义,它在 IR 中应该是这个样子:
xxxxxxxxxxdeclare i64 @init_array(i32, i64)# ...entry:%11 = call i64 @init_array(i32 %10, i64 0)
4.7.9 Loop Translation
对于 while 语句,简单地转换为分支和 goto:
xxxxxxxxxxtest: if not(condition) goto done body goto testdone:另外,我们需要注意 loop 中的 break 只能跳出当前层,并且不能有两个 break 在一个 body 中;
我们可以通过维护 std::stack<llvm::BasicBlock *> break_stack,然后在遇到 break 时找栈顶的 block 位置并跳到它的 done 标签位置即可;
for 语句类似地重写为:
xxxxxxxxxxlet var i := lo var limit := hiin while i<= limit do (body; i := i + 1)end注意 overflow 的问题;
4.7.10 Function Translation
注意到我们希望一个函数被翻译成这个 IR:
xxxxxxxxxx%99 = call i32 @func(i64 %sp, i64 %sl, i32 %actual_parm13, i32 %actual_parm15, i32 %actual_parm17)前两个参数分别是插入的、被我们自己计算和管理的旧栈顶指针,以及 static link 的值;
回忆一下,static link 是借助
func的 Level 以及调用func的函数的 Level 来计算的;
另外需要注意一个概念:Outgoing space。第三次回忆 Tiger 的栈帧分布:

arguments 和 static link 的空间统称为 outgoing arguments,这部分空间由 caller 为 callee 准备的,caller 本身不用,但是又属于 caller 的栈帧,因此被称为 caller 的 outgoing space;
我们在 IR Builder 中需要手动分配一下这块区域:
xxxxxxxxxxlevel->frame_->AllocOutgoSpace(outgo_arg * reg_manager->WordSize());注意 Tiger Compiler 暂时把全部的参数都放到栈上而非寄存器传递。
4.7.11 Declaration Translation
在 Translation 阶段对于 declarations 的处理和 semantic analysis 相似,不过实际翻译时需要加一个 level 参数(例如在处理函数时判断深调浅还是浅调深):
xxxxxxxxxxvoid Dec::Translate(env::VEnvPtr venv, env::TEnvPtr tenv, tr::Level *level) const = 0;如果是 variable declaration,那么更新
venv以及初始化某些值;如果是 type declaration,那么更新
tenv;如果是 function declaration,那么:
创建一个函数,做法很像之前创建
init_array;然后把
FuncEntry插入venv;然后创建 framesize 的全局变量
@func_name_framesize_global,设置到fun_level->frame_->framesize_global,并且初始化为 0;因为函数的 frame size 目前不一定是常量;
添加动作:更新新的
sp值:xxxxxxxxxxfun_level->set_sp(ir_builder->CreateSub(sp_arg_val, func_framesize));构建
bodybasic block;添加动作:将各个参数值存放到各自的
InFrameAddress地址中;继续翻译
bodybasic block,最终创建ret指令;现在 Frame Size 才决定下来,将值设置回去:
xxxxxxxxxx// 大概值,因为还需要对齐问题(level->frame_->offset_ + level->frame_->outgo_size_) / 16 * 16 + 8;
Chapter 5. Instruction Selection
翻译工作结束后,程序的 IR 树就彻底生成了,现在距离真正的机器代码还有一步之遥:我们需要把 IR Structure 映射到机器代码上,这步就被称为 “指令选择”(Instruction Selection)。
注意,一条指令可以覆盖多个 IR 结构,例如 mov 8(%rax, %rbx, 4), %rsi 覆盖了一次 mul、2 次 add 和一次 load IR 结点;
5.1 Theories: Jouette Architecture & Selection Methods
我们先从理论角度讨论指令选择:Jouette Architecture;它满足如下性质:
load / store架构;相对更大的通用寄存器(可存放数据 / 地址),每个指令可以访问任何寄存器;
每条指令时延 1 cycle(除了
movem,这条指令在真实实现中不会存在);一个 cycle 只会执行一条指令;
那么代码 a[i] := x(i 位于寄存器,a,x 在 stack frame 中)IR 树可以抽象表示为(如果不含有类型信息):
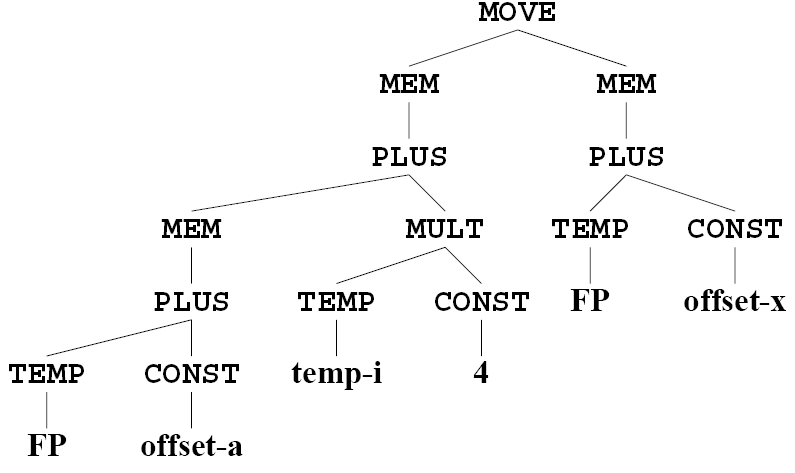
注:
x在 stack frame 中,因此需要 Frame Pointer 和访存完成读取;
因此即便是弱类型的编译语言,也只是把判断的操作推迟到指令生成这步来判断;
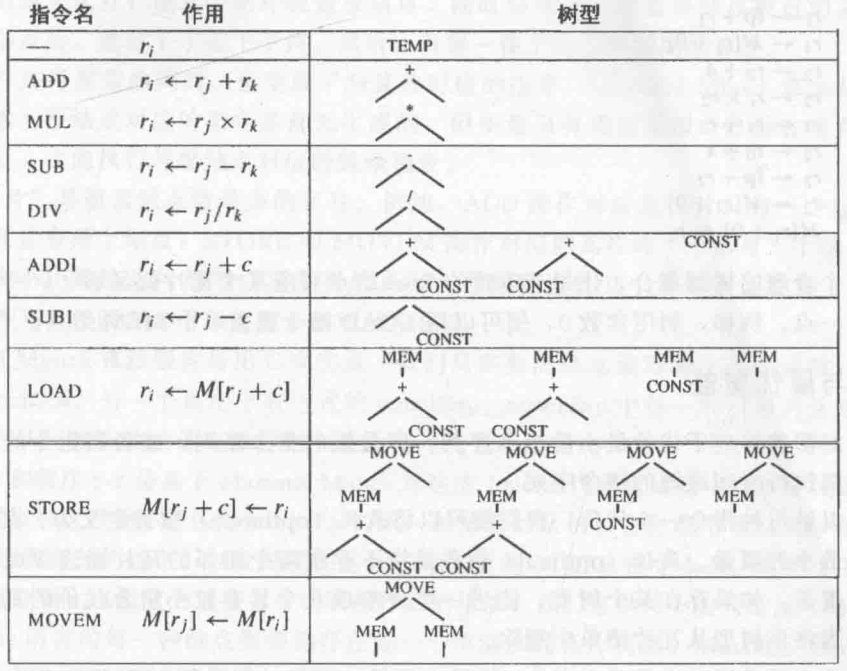
注意:以
MOVE为例,它的左右两个子树分支的含义是不一样的(srcvsdst),不能随便互换;
就有两种 tiling 方式:
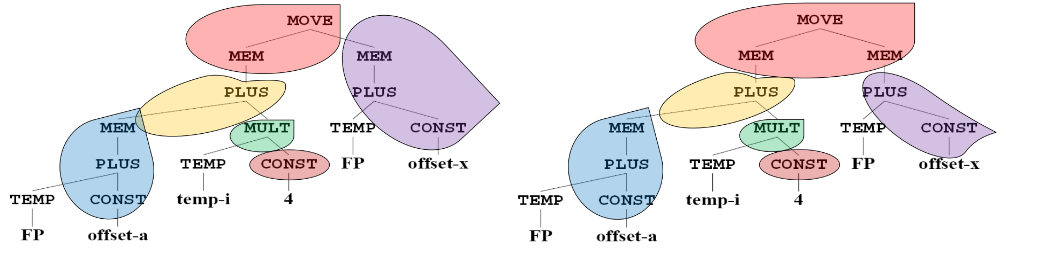
分别对应两种指令选择方式:
xxxxxxxxxxLOAD r1 = M[fp+a]ADDI r2 = r0 + 4MUL r2 = ri * r2ADD r1 = r1 + r2LOAD r2 = M[fp+x]STORE M[r1] = r2
# 或者LOAD r1 = M[fp + a]ADDI r2 = r0 + 4MUL r2 = ri * r2ADD r1 = r1 + r2ADDI r2 = fp + xMOVEM M[r1] = M[r2] 即便是这么简单的指令也有两种指令选择方式,更不用说实际情况下的代码的复杂性了。那么我们怎么判断一个指令选择是好是坏?
我们在前提中假设,Jouette Architecture 中每条指令执行时延为 1 个 cycle,并且每个 cycle 只能执行一条指令,因此在保持语义不变的情况下,指令数越少,指令选择产生的代码效率越高;
再由于指令选择的多样性,我们必然有局部最优(好实现)和全局最优的情况。局部最优和全局最优在 RISC 系列架构下差别不大(每条指令执行时间相近,并且可选择的组合/搜索空间本身不多),但是对于 CISC 系列架构就截然不同了!主要是每条指令的执行时间差别很大。
这里介绍一种局部最优的指令选择算法:Maximal Munch(贪心策略)。先 top-down 地划分尽可能大的 tiling(Cover root node of IR tree with largest tile t that fits),然后递归对子树重复这个操作;在覆盖完成后,bottom-up 地生成指令即可;
再介绍一种全局最优的指令选择算法:Dynamic Programming(动态规划)。我们使用 bottom-up 的计算方法,在计算树根前就已经计算出子树(子问题)的 cost 情况。
特别地,我们记 cost 为 c 的 tile 匹配 node n 时的 cost 为
例如对这个 IR:MEM(PLUS(CONST(1), CONST(2))),我们生成的迭代情况如下:
| Stage | Tile | instruction | Tile Cost | Leaves Cost | Total cost |
|---|---|---|---|---|---|
| 1 | - (+) - | ADD | 1 | 1+1 | 3 |
| 1 | CONST - (+) - | ADDI | 1 | 1 | 2 |
| 1 | - (+) - CONST | ADDI | 1 | 1 | 2 |
| 2 | (MEM) - | LOAD | 1 | 2 (Min of last iteration) | 3 |
| 2 | (MEM) - + - CONST - | LOAD | 1 | 1 | 2 |
| 2 | (MEM) - + - - CONST | LOAD | 1 | 1 | 2 |
注意到不同 iteration 中可以深入之前的内部结构进行匹配(主要是遍历 Jouette Instructions);
注:当然,考试时也可以不使用这种列表的方法,直接在树上 bottom-up 地标记 “以指定节点为根的最小 cost”,顺便在旁边记录一下这种划分方式。这种解法可以极大的节省绘制表格的时间(感谢 @kiwi 提供的思路)。
5.2 Practice I: LLVM-based Instruction Selection
在 LLVM 中如何做 Instruction Selection?
以 a[i] := x 为例,假设 i 在变量 %1 中,x 在 frame 的 (fp + 16) 位置,a 在 %2 中,对应的 IR Tree 如下:
xxxxxxxxxx%3 = getelementptr i64, i64* %2, i64 %1%4 = add i64 %sp, 16%x_ptr = inttoptr i64 %4 to i64*%5 = load i64, i64* %x_ptr, align 4store i64 %5, i64* %3, align 4现在我们希望从上述 IR Tree 中抽取 tiles:
xxxxxxxxxx# %3 = getelementptr i64, i64* %2, i64 %1movq t223,t225movq t224,%raximul $8, %raxaddq %rax,t225
# %4 = add i64 %sp, 16# %x_ptr = inttoptr i64 %4 to i64*leaq 16(%rsp),t226
# %5 = load i64, i64* %x_ptr, align 4movq (t226),t227
# store i64 %5, i64* %3, align 4movq t227,(t225)另一种生成 tiles 的方法是:
xxxxxxxxxx# %3 = getelementptr i64, i64* %2, i64 %1movq t223,t225movq t224,%raximul $8, %raxaddq %rax,t225
# %4 = add i64 %sp, 16# %x_ptr = inttoptr i64 %4 to i64*# %5 = load i64, i64* %x_ptr, align 4movq 16(%rsp),t226
# store i64 %5, i64* %3, align 4movq t226,(t225)后者显然更好一些。
但我们发现,直接用上面的 LLVM IR List 不方便追踪各个结点间的数据依赖,因此我们可以把这个 tiling 表示为一棵 DAG:
也就是说,对每个 LLVM Basic Block,将 LLVM IR List 转换为一个 selection DAG,返回值是 root node;
这样我们在进行 optimal/optimum search 时尝试对 root node 选最大的 tile,然后递归对每个 out-edges(出边)重复操作(也就是之前的 maximal munch 方法);
因此在 LLVM 中,实现 Maximal Munch 比较困难,因为我们需要将 LLVM List 转为 Selection DAG,并且这次每个叶结点的 cost 不再是 1 了;
5.3 Practice II: Instruction Selection for the Tiger Compiler
首先我们需要明确一点,我们之前生成 LLVM IR 后,已经可以借助 LLVM 后端生成机器代码了。但是如果我们需要从 LLVM IR 利用自己写的编译器后端生成机器代码,那么就需要手动解析 LLVM IR,抛弃一部分约定(例如之前的 outgoing space)、抛弃 LLVM 的封装(从 llvm::Value* 中取出)并完全由自己管理寄存器和栈。
5.3.1 Targets & Preparations
在指令选择阶段,Tiger Compiler 需要完成哪些任务?
存储程序信息:我们知道,x86(-64) 中常量通常存放在
.rodata中,并且通过%rip相对地址访问;也就是 compiler 需要指定.rodata段,并且生成一个 Label 以供 linker 在 relocation 阶段生成实际地址;此外 compiler 还需要指定
.text并将之后生成的代码放入其中;注:与汇编节位置有关的代码会被
frame::Frags管理起来。这样有助于分别实现生成代码的区域。frame::StringFrag:描述全局字符串的汇编块;frame::ProcFrag:每个函数实现块会生成一个这样的汇编块;frame::FrameSizeFrag:在指令选择过程中,我们会把 global frame size 常量像字符串常量一样放在 global section 中,它们用这样的汇编块描述;
存储字符串常量:需要包含一个 label 区别所有的 string constant、string length 声明、string chars;
存储 framesize:在生成的代码中,将 translate 阶段计算好的 global frame size 生成为一个 label 和一个值;
而在生成 frame::ProcFrag 前,我们需要做一些额外的工作:
Generate Register Numbers
我们回忆,在 translation 阶段,我们由 LLVM IR Builder 生成的都是虚拟寄存器。而在指令选择阶段,我们需要转换成实际的寄存器。但是我们知道,一个体系架构中的有限寄存器会影响我们的分析(例如要思考这个寄存器什么时候要被重复利用、是否能被利用,等等)。
于是索性我们继续把问题向后放,在指令选择阶段仍然认为寄存器无限,在生成完汇编指令后再统一处理成有限寄存器。
不过,现在在指令选择阶段,即便我们认为寄存器数量无限,还是要把 LLVM IR 中的虚拟寄存器换掉。因为在 LLVM IR 中,每个函数内部会重新对虚拟寄存器编号。如果不作处理,在翻译成汇编后会出现冲突的情况。
于是我们定义了一个类 TempFactory,用于临时生成这些寄存器编号(工厂模式)。
Instruction Wrapper
其次,我们需要定义一个对指令生成的 wrapper,可以获取当前指令用到的寄存器、新使用的寄存器,以及打印这个指令的方法:
xxxxxxxxxxunder namespace assem:class Instr {public: // 写入哪些寄存器 [[nodiscard]] virtual temp::TempList *Def() const = 0; // 从哪些寄存器中读 [[nodiscard]] virtual temp::TempList *Use() const = 0; // temp::Map 存放的是全局临时寄存器(TempFactory 分配的)和 物理寄存器 的映射关系 virtual void Print(FILE *out, temp::Map *m) const = 0;}以 movq (t200), t201 为例,假设这条指令对应的 Instr 对象是 instr1,那么 instr1.Def() 就是 [t201],instr1.Use() 就是 [t200];
Def, Use可以在寄存器优化 / 寄存器时起作用;
注意到 temp::Map 只是一个将 Temp 映射到 std::string 的 Table,并且具有 scope 覆盖的能力:
xxxxxxxxxx /* temp.h under namespace temp: */class Map {public: // ... void Enter(Temp *t, std::string *s); std::string *Look(Temp *t); static Map *Empty(); static Map *LayerMap(Map *over, Map *under); private: tab::Table<Temp, std::string> *tab_; Map *under_; Map() : tab_(new tab::Table<Temp, std::string>()), under_(nullptr) {} Map(tab::Table<Temp, std::string> *tab, Map *under) : tab_(tab), under_(under) {}};
temp::Map可以有 debug、帮助后面寄存器分配的作用。
注意到,Instr 可以有很多子类补充它的含义,例如:
OperInstr(操作指令,大多数指令都是它,包括 LLVM IR 的load / store / mov、四则运算):xxxxxxxxxxclass OperInstr : public Instr {public:// 这条指令从 LLVM IR 转换到 assembly 的结果std::string assem_;// 应对 x86 指令的复杂性,使用列表存储 source & destination// 例如 mov %rax, (%rdx) 中,两个寄存器都是 src,没有 dsttemp::TempList *dst_, *src_;Targets *jumps_;OperInstr(std::string assem, temp::TempList *dst, temp::TempList *src,Targets *jumps): assem_(std::move(assem)), dst_(dst), src_(src), jumps_(jumps) {}/* ...... (more) */};这种操作指令在生成 assembly 后 fall through 到下一条
jumps_ == nullptr的指令中去;因为
jumps_ != nullptr可能是分支跳转,应该由其他的Instr(例如LabelInstr,会另外处理 Label 事宜,并指定跳到哪里去)处理;举一些例子,比如
%3 = load i64, i64* %2, align 4LLVM IR 可以转换为:xxxxxxxxxxassem::OperInstr(// 这里 “`” 的作用是模板字符串,在之后确定下寄存器编号后,再进行字符串替换// 因此注意到,初始化传入的是模板!"movq (`s0),`d0",// 无限寄存器假设下,对于 Def register,总是先分配一个新的寄存器temp::TempList(temp::TempFactory::NewTemp()),// 从上述 LLVM IR 中拿到 %2 代表的指针,并且在 temp Map 中找到对应的 temp::Temp(List)// 后面会讨论如何建立 LLVM IR 虚拟寄存器 和 Temp 全局临时寄存器的映射temp_map_->find(load_inst.getPointerOperand())->second,nullptr);当然,通过
temp_map_映射的不同虚拟寄存器,在最终翻译的时候可能出现相同的情况,例如指令%5 = mul i32 %2, %4在转为OperInstr后发现dst = [t908],src = [t908,t909],此时在最终翻译时就能充分利用这个性质,生成类似imul %rsi, %rdi这种自乘的指令;再例如,如果在 LLVM IR 中本身 源虚拟寄存器和目标虚拟寄存器 就有相同的,如语义
t1 <- t1 + t2,,那么翻译成OperInstr时src = [t1,t2], dst = [t1];MoveInstr(寄存器移动指令,它理论上可以没有。只不过用来做优化比较方便而已),考虑两个寄存器间的移动的情况,如果src和dst是相同的,那么会直接删除,方便优化过程;LabelInstr(标签跳转指令,它通常不存在源寄存器和目标寄存器,仅当<label-name>:\n的情况出现):xxxxxxxxxxclass LabelInstr : public Instr {public:std::string assem_;temp::Label *label_;LabelInstr(std::string assem): assem_(std::move(assem)), label_(temp::LabelFactory::NamedLabel(assem)) {}/* ...... (more) */};
BB Jump Wrapper
另外,我们不仅需要对指令生成进行包装,还需要对 Basic Block 的跳转情况进行记录,这个跳转情况使用 Target 类型保存:
xxxxxxxxxxclass Targets {public: // 可能因为分支较多,有多个可能跳向的 label std::vector<temp::Label *> *labels_; explicit Targets(std::vector<temp::Label *> *labels) : labels_(labels) {}};De-duplicate Labels
将 basic block 的 label 重命名为全局唯一的 label。主要是因为 LLVM 在翻译阶段只保证了每个函数中的 label 唯一:

这个生成新的 Label 的工作交由 LabelFactory 和 Label 类型完成。
Code Generation Wrapper in Frame Level
首先明确一下,我们在生成 LLVM IR 后,除了全局变量,其他的代码都被生成到了特定的 frame 中(或者说函数中)。
在 frame 粒度下,我们包装一层用于生成这个 frame 下汇编代码的类型 CodeGen,作为本轮指令选择阶段的入口函数:
xxxxxxxxxx/* codegen.h */namespace cg {class CodeGen {public: // 注意到,LLVM IR builder 在为函数生成 basic block 时使用 canon::Traces,我们同样在这里使用这个类型作为参数, // 方便我们从 LLVM 那里获取帮我们拆好的一组 basic blocks CodeGen(frame::Frame *frame, std::unique_ptr<canon::Traces> traces) : frame_(frame), traces_(std::move(traces)) {} void Codegen();private: frame::Frame *frame_; std::unique_ptr<canon::Traces> traces_; // 最终我们会逐个 basic block 生成指令列表 std::unique_ptr<assem::InstrList> assem_instr_;};}主要代码入口:
xxxxxxxxxx/* codegen.cc */namespace cg {void CodeGen::Codegen() { auto *list = new assem::InstrList(); for (auto &&bb : traces_->GetBasicBlockList()->GetList()) { // ...... (more) // main routine of code generation for (auto &&inst : bb->getInstList()) InstrSel(list, inst, traces_->GetFunctionName(), bb); } // 函数收尾工作。我们后面讨论 assem_instr_ = std::make_unique<AssemInstr>(frame::ProcEntryExit2( frame::ProcEntryExit1(traces_->GetFunctionName(), list)) );}}Function Entry/Exit
再次注意,现在翻译成 LLVM IR,除了全局变量,其他代码都在函数中了!
在 CodeGen 类中,我们讨论到代码会在一个 frame 结束后进行收尾工作。这里我们讨论一下翻译 functions 时,在进入和退出需要做哪些额外工作(这不仅仅在 Tiger 中,在其他语言中也会存在)。处理 functions 主要分为 3 个阶段:
Prologue
伪指令声明函数开始(便于生成符号表、便于链接器识别等等);
xxxxxxxxxx.text # 指定代码段.type P, @function # 声明符号类型为函数开始准备一个 Label;
调整栈指针
%sp(tiger compiler 已经在 translation 阶段生成好了);将 escaping variable(包括 static link)放到栈帧上,把 non-escaping variable 分配到新的临时寄存器中;
把 callee-saved registers push 到栈上,这样它们就可以参与 function body 的寄存器分配了,而无需担心打乱其中的数据的问题(注:GCC 的方案是用到哪个 push 哪个);
注意:这些 callee-saved registers 的保存和恢复过程需要事先写成真实物理寄存器!
Body
Epilogue
将函数返回值移动到 当前体系结构的 calling convention 约定的返回值寄存器中(例如 x86-64 就是
%rax);恢复之前 backup 的 callee-saved registers;
重置栈指针
%sp(释放栈空间);注意
ret汇编指令(LLVM IR 中没有!);(optional,有些体系结构或者链接器需要)伪指令声明函数结束;
我们发现上述阶段在不同的地方或多或少地已经被完成了,例如:
prologue 1/2/3 和 epilogue 3/4/5,有些取决于 frame size 的具体大小(prologue 3 & epilogue 3),我们认为应该在
frame::ProcEntryExit3中完成;Important
即便在指令选择阶段,我们仍然不能知道 frame size 的大小!因为还需要等到具体寄存器分配(分配真正的物理寄存器)这个阶段才能确定,因为可能出现 register spilling 现象,它同样可能扩2大 frame size;
prologue 5 和 epilogue 2,关于 callee-saved registers 的保存问题,都属于 view shift 的一部分,我们认为应该在
assem::InstrList *frame::ProcEntryExit1(std::string_view function_name, assem::InstrList *body)中完成;prologue 4 发生在 function body 解析之前,我们在这里还要记录 LLVM values 和
temp::Temp(全局临时寄存器)的映射关系(回想之前temp_map_);epilogue 1 会在函数 body 解析完成后执行,作用与 LLVM IR 的
ret指令等价;
我们现在来讨论,上述步骤对应的 frame::ProcEntryExit1/2/3 的具体实现。
frame::ProcEntryExit1:enter:保存 callee-saved registers 到栈上,让它们参与寄存器分配;
exit:恢复 callee-saved registers 的值;
xxxxxxxxxxprocedure ProcEntryExit1:enter: move all the callee-saved registers to temp::TempFactory::NewTemp()exit: restore all the callee-saved registers from previous temp::TempListframe::ProcEntryExit2:关于寄存器分配相关工作。检查退出函数时,有哪些寄存器仍然存活(涉及寄存器生命周期,后面讨论);xxxxxxxxxxassem::InstrList *ProcEntryExit2(assem::InstrList *body);/* xxframe.cc */temp::TempList *xxRegManager::ReturnSink() {temp::TempList *temp_list = CalleeSaves();temp_list->Append(StackPointer());temp_list->Append(ReturnValue());return temp_list;}assem::InstrList *ProcEntryExit2(assem::InstrList *body) {// 提示除了 callee-saved registers,还有保存 stack pointer、return value 的 register 可用(存活)body->Append(new assem::OperInstr("", new temp::TempList(),reg_manager->ReturnSink(), nullptr));return body;}frame::ProcEntryExit3:(enter)伪指令声明函数开始;
(enter)函数开始的标签;
(enter)调整栈指针
%sp;(exit)重置栈指针
%sp;(exit)生成
ret汇编指令(为什么不在函数体内生成,我们后面讨论);(exit,optional)伪指令声明函数结束;
xxxxxxxxxx# 应该生成:tigermain:movq tigermain_framesize_global(%rip), %raxsubq %rax,%rsp# ...movq tigermain_framesize_global(%rip), %rdiaddq %rdi,%rspretq
No Frame Pointer in Tiger
注意到,tiger compiler 使用的是虚拟的 frame pointer(使用 stack pointer 进行计算)。
我们在 translation 阶段使用 frame pointer(FP)和每个变量的 offset(k)来指代 InFrame Variable,并且已经把 FP 表示法更换为 SP + k + frame size 表示法(仍然用 frame size 变量,因为目前还确定不了)。
那么在指令选择阶段需要注意,funcName_framesize_global 全局变量由 frame::FrameSizeFrag 生成;
Register Mapping
此外,对每个物理寄存器,我们需要将一个代表它的字符串(方便生成汇编),以及一个对应的 temp::Temp 全局临时寄存器 对应起来。
temp::Temp Mappings
另外,我们需要在正式生成 function body 代码前(CodeGen::CodeGen() 构造时),进行 temp::Temp 的映射的构建。主要有几个部分:
每个 LLVM Instruction 中虚拟寄存器和
temp::Temp的映射;全局字符串和
temp::Temp的映射(为了简化实现,我们统一把 Global String 地址放在temp::Temp,随用随取);把 escaping 和 non-escaping 变量从 LLVM
CreateCall指定的参数寄存器传递到被temp::Temp管理的寄存器中(也是为了方便后面的取用);因为需要脱离 LLVM IR,我们必然无法保留 outgoing space,必须在机器指令
call前准备好寄存器、栈区域。
对于第一个部分,回忆之前实现 OperInstr 的问题,我们需要把 LLVM IR 中代表的虚拟寄存器 和 在指令选择阶段分配的 temp::Temp 关联起来,以支持指令选择的数据依赖。
我们观察到,LLVM IR 中,存在等式的 IR 语句中,左边的部分(称为 “LLVM Instruction 的 return value”)就是在新建一个虚拟寄存器,因此我们在指令选择阶段,就能在遇到每个存在 return value 的 LLVM Instruction 时,都向 temp_map_ 插入 llvm::Value* 和 temp::Temp(新建的)的映射。
xxxxxxxxxxfor (auto &&bb : traces_->GetBasicBlockList()->GetList()) { // record every return value from LLVM instruction for (auto &&inst : bb->getInstList()) temp_map_->insert({ &inst, temp::TempFactory::NewTemp() });}于是获取 llvm::Value* 时,想获得它对应的 temp::Temp 寄存器,就直接向 temp_map_ 查找就行:
xxxxxxxxxx// 例如语句:%init_sp = sub i64 %0, %init_local_framesizeauto *value = llvm::dyn_cast<llvm::Value>(sub_inst.getOperand(0));auto tmp = temp_map_->find(value)->second;对于第二个部分,我们还需要将全局字符串的地址提前计算到 temp::Temp 中,然后把字符串对应的 llvm::Value* 和这个寄存器对应起来,方便之后直接使用。
xxxxxxxxxx// firstly get all global string's locationfor (auto &&frag : frags->GetList()) { // for each StringFrag if (auto *str_frag = dynamic_cast<frame::StringFrag *>(frag)) { auto tmp = temp::TempFactory::NewTemp(); list->Append(new assem::OperInstr( // use string name as label & %rip to get the runtime address "leaq " + std::string(str_frag->str_val_->getName()) + "(%rip),`d0", // put the string address to the allocated register new temp::TempList(tmp), new temp::TempList(), nullptr )); // insert into temp_map_ for OperInstr to use! temp_map_->insert({str_frag->str_val_, tmp}); }}对于第三个部分,我们从 LLVM 语句中获取传参的寄存器信息,并且把它们表示的 llvm::Value* 映射到 temp::Temp 中,这样做是为了函数体的解析做准备;
xxxxxxxxxx// 对寄存器传参for (; arg_iter != traces_->GetBody()->arg_end() && // regs 是当前体系结构 calling convention 规定的参数物理寄存器 tmp_iter != regs->GetList().end(); ++arg_iter, ++tmp_iter) { auto tmp = temp::TempFactory::NewTemp(); list->Append(new assem::OperInstr( "movq `s0,`d0", new temp::TempList(tmp), new temp::TempList(*tmp_iter), nullptr )); temp_map_->insert({static_cast<llvm::Value *>(arg_iter), tmp});}
// 如果实际 LLVM IR 传参数量多于 regs 大小,需要放到栈上// Assume the register last_sp’s value is (%rsp + framesize)while (arg_iter != traces_->GetBody()->arg_end()) { auto tmp = temp::TempFactory::NewTemp(); list->Append(new assem::OperInstr( "movq " + std::to_string(8 * (arg_iter - traces_->GetBody()->arg_begin())) + "(`s0),`d0", new temp::TempList(tmp), new temp::TempList(last_sp), nullptr )); temp_map_->insert({static_cast<llvm::Value *>(arg_iter), tmp}); ++arg_iter;}
%my_sp Management
还要注意一个问题,在 LLVM translation 阶段中,我们手动管理的 %sp:
作为每个非库函数的第一个参数;
每次在函数内手动计算;
现在要转成机器代码时需要抛弃它,并且转换成真实的 %rsp(x86-64);
不过庆幸的是,我们在 translation 阶段生成的 %sp 计算的指令是可以直接复用的,也就是说,我们只需要在指令选择解析函数调用时:
跳过非库函数的第一个参数(我们之前管理的
%funcName_sp)的传递(不放到寄存器或者栈上);直接把所有
%funcName_sp(第一参数)的出现换成%rsp;注意所有涉及
%funcName_sp的运算!我们可以定义一个函数识别一下:xxxxxxxxxx// check if the value is %my_sp in LLVMbool IsRsp(llvm::Value *val, std::string_view function_name) const {// ...}
另外,不用担心在当前函数外的 %rsp 的状态,因为这被前面提到的 frame::ProcEntryExit3 管理。
5.3.2 Generate from LLVM Instructions
现在我们终于处理完一些琐碎的准备工作,可以正式着手从 LLVM IR 中的 instruction 生成平台对应的指令了。
llvm::Instruction::Load
假设 LLVM IR 为 %10 = load i32, i32* %N_ptr, align 4,生成步骤如下:
从 LLVM Instruction 中获取
%N_ptr的llvm::Value*;将涉及的所有寄存器转为自管理的
temp::Temp(如%10和%N_ptr都通过查表temp_map_获取。temp_map_已经在之前的叙述中介绍过了构建方法和时机);生成这条指令的原义(例如在 x86-64 下
mov (t101), t102,通过OperInstr给出。其中t101/t102是上一步得到的temp::Temp);
llvm::Instruction::Add/Sub/Mul/SDiv
假设 LLVM IR 为 %8 = add i64 %7, -8,生成步骤如下:
获取操作数(operands)对应的
llvm::Value*,并查表把它们映射到temp::Temp;注:在 LLVM 中
getOperand()能获取 LLVM IR 的操作数的llvm::Value*;根据操作数类型选择合适的指令(例如在 x86-64 中,这条指令用
addq还是leaq);
llvm::Instruction::Call
假设 LLVM IR 为 %84 = call i32 @bsearch(i64 %bsearch_sp, i64 %83),生成步骤如下:
跳过第一个参数
%bsearch_sp(参见上文 “%my_spmanagement”);将所有应该通过栈传递的参数放到栈上(其他遵循 x86-64 calling convention,直接通过寄存器传参);
生成汇编
call指令;注:在 LLVM 中
getCalledFunction()->getName()能获得 LLVM IR 当前 Call 指令的函数名称;从 calling convention 规定的寄存器(例如 x86-64 是
%rax)中获取返回值;
llvm::Instruction::Ret
假设 LLVM IR 为 ret i32 %47,生成步骤如下:
从
llvm::Value*获得temp::Temp,并把temp::Temp中的值移动到物理寄存器%rax(对 x86-64 的 calling convention)对应的temp::Temp中;跳至 exit label(exit label 的创建由前文提到的
frame::ProcEntryExit3完成);为什么不直接生成
ret,而交由frame::ProcEntryExit3生成 exit label 并跳转呢?考虑一种情况:假设一个函数体内有多个
return,如果每次都生成一次 调整%sp和ret汇编,则会造成代码冗余,因此不如在函数汇编结尾统一生成后处理的指令,把这个逻辑包装成frame::ProcEntryExit3;
llvm::Instruction::ICmp
假设 LLVM IR 为 %20 = icmp eq i64 %19, 0,生成步骤如下:
获得所有 operands 对应的
temp::Temp;根据当前指令的比较条件生成比较的汇编指令(像 x86-64 的
cmpq会改变 condition codes / flag registers);生成
set类指令向 instruction return value 对应的temp::Temp设置值(如 x86-64 会根据 condition codes 来设置);
例如上面的例子会生成:
xxxxxxxxxxcmpq t19, $0sete t20
llvm::Instruction::Br
假设 LLVM IR 为 br i1 %20, label %if_then, label %if_else,生成步骤如下:
获取 condition
%20的temp::Temp;根据 condition 的全局临时寄存器(0 还是 1),生成 jump 指令跳至对应的 label(例如
jXX);
llvm::Instruction::Phi
假设 LLVM IR 为:
xxxxxxxxxxopand_next: ; preds = %opand_right_test, %isdigit %42 = phi i1 [ false, %isdigit ], [ %41, %opand_right_test ]我们知道,如果 PC 是从 %isdigit 标签跳来的,那么 %42 的值是 0,如果是从 %opand_right_test 跳来的,那么 %42 的值是 1。问题是,我们要转为汇编指令,如何知道 PC 是从哪里来的?phi 应该如何实现?
我们来看看 LLVM 自己的后端怎么解析这个 IR 的。它的策略是,在汇编层面把赋值语句前移,例如这样一段 LLVM IR:
xxxxxxxxxxopand_right_test: ; ... br label %opand_nextisdigit: ; ... br label %opand_nextopand_next: ; preds = %opand_right_test, %isdigit %42 = phi i1 [ false, %isdigit ], [ %41, %opand_right_test ]翻译成:
xxxxxxxxxxopand_right_test: movq 0, t43 jmp opand_nextisdigit: movq t41, t43 jmp opand_nextopand_next: movq t43, t42这种做法的思路很简单,但是困难点在于,LLVM 解析后的 Basic Blocks 放在列表中,并且不容易查看这些 blocks 的关系、不知道 phi 可以从哪个 block 来,因此也就没法清楚地知道可以向哪些 blocks 中插入 move 指令了。
一种处理方法是,记录每个 Basic Block 的 Index。在每个函数开始时,遍历 LLVM 帮我们保管的所有 basic blocks(canon::Traces 类型,每个 CodeGen 都会保存。traces_->GetBasicBlockList()),将每个 basic blocks 编号并放入映射表中;
然后每次进行 Br 跳转时,将 Basic Block Index 放入 %rax 中(相当于传参),这样在解析到 phi 指令时可以通过读取 %rax 来判断是从哪个 basic block 跳转而来;
上面相同的 IR 可以翻译为:
xxxxxxxxxxcmp $2,%rax ; 假设其中一个 basic block 是 2,另一个是 8je bsearch_if_next_1804289383 ; hash 生成一个临时的 label,方便 merge value 时进行跳转cmp $8,%raxje bsearch_if_next_846930886bsearch_if_next_1804289383: movq t318,t338 jmp bsearch_if_next_endbsearch_if_next_846930886: movq t409,t338 jmp bsearch_if_next_endbsearch_if_next_end:Other Instructions
例如:llvm::Instruction::PtrToInt/IntToPtr、llvm::Instruction::GetElementPtr、llvm::Instruction::BitCast/ZExt;
Chapter 6. Local & Global Optimizations
在生成完目标平台的汇编代码后,除了寄存器分配的问题没有解决,这个生成的代码已经能够跑在一个解释器上了。
我们现在的目标是对现在编译器生成的汇编代码进行优化。
优化的前提是需要保证正确性。不正确的程序运行地再快也没用。
6.1 Preparations
先介绍一些帮助优化的基本概念。
首先是从编译器的角度来看一个变量的生命周期。
如果满足下述情况,则称一个变量 x 在语句 s 中是 live 的:
存在一个使用
x的语句s';存在一个从
s到s'的执行路径;这个执行路径上不存在对
x赋值的语句;
而一个语句 x := ... 在 x 死亡后也被视作死亡。
一个死亡的语句可以直接从程序中被删除,而不会影响正确性。这就是 “死代码削除”;
但是 “存在一个执行路径” 并不好查找。因为一旦存在循环结构,执行的路径数就会爆炸,这个正确性是不能保证的。
而且对于非局部的变量而言,判断上述条件需要全局分析;
6.1.2 Definition: Local Optimizations
定义;发生在一个 Basic block 中的优化操作;
种类:
常量传播/折叠(constant propagation / folding);
局部死代码删除(local dead code elimination):
局部相似子表达式复用(Local Common Subexpression Elimination);
6.1.3 Definition: Global Optimizations
全局优化过程可以扩展到整个 control-flow graph(CFG);
种类:
代码移动(code motion);
循环结构转换(loop transformation);
内联化(inlining);
全局死代码删除、相似子表达式复用(与局部相对);
6.2 Global Analysis
6.2.1 Example: Liveness Check
全局分析的主要思路是,把一个复杂程序的每个语句的性质视作其前驱和后继的共同作用。
这样我们只需要使用一行行的递归就能实现整个程序代码的解析的效果。因此我们定义:
于是以全局分析的 Liveness Check 为例,我们可以总结一些存活规则:
如果语句
如果语句
如果语句

于是有检测某个变量及对应语句存活的算法:
所有
从后向前循环检查所有 statements,遇到满足上述存活规则的则进行更新,直至当前轮循环不对任何
举个例子:
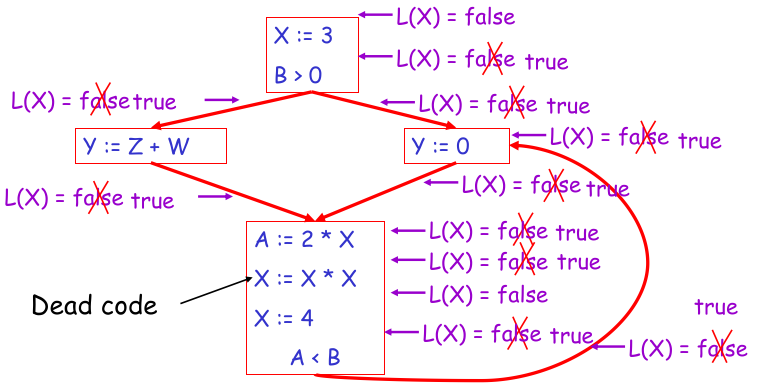
这幅图有个名字:程序的控制流图(Control-Flow Graph,CFG);不过这个定义不严谨,我们后面讨论。
注:我们一般是从末尾向前依次检查,并且只有从
false改到true的情况,不存在true到false的情况,每个最多只会被更改一次。因此上述算法的时间复杂度为线性的; 于是我们通过上面的分析可以发现
x := x * x是死代码,可以直接删除;
我们知道了一个变量的存活检测方法,那么多个变量的呢?答案是建立一个集合 Liveness set。我们定义:
Use[s]指令Def[s]指令In[s]进入指令Out[s]指令
于是我们可以总结上面的规则为两个公式:
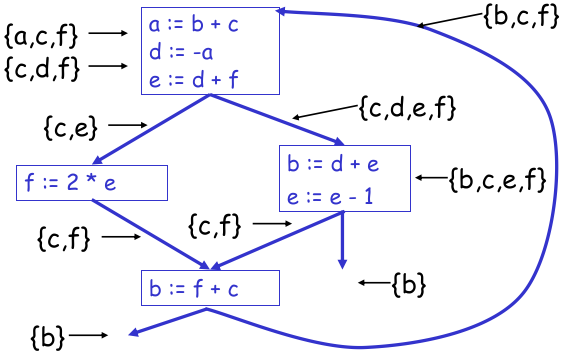
6.2.2 Forward & Backward Analysis: Constant Propagation as an Example
我们在之前做 Liveness check 时发现它是从程序结尾向前检查的,这种分析方式被称为 backward analysis;
相对地,像对 constant propagation 这种检查的方式是 forward analysis(从代码开始向后检查);
现在我们讨论一下 constant propagation 的实现。它是如何保证正确性的?
我们先简单描述一下规则:在所有用到
我们描述的更准确一些,一个变量
#表示;c表示(x := constant c);并不清楚
*表示;
同样我们类似地定义
如果
如果
如果
如果
(以上关注 instruction 间的关系)以及(以下关注 instruction 前后的关系):
如果
如果
如果
进一步地,这个规则可以通过部分内联化得到缓解。
如果
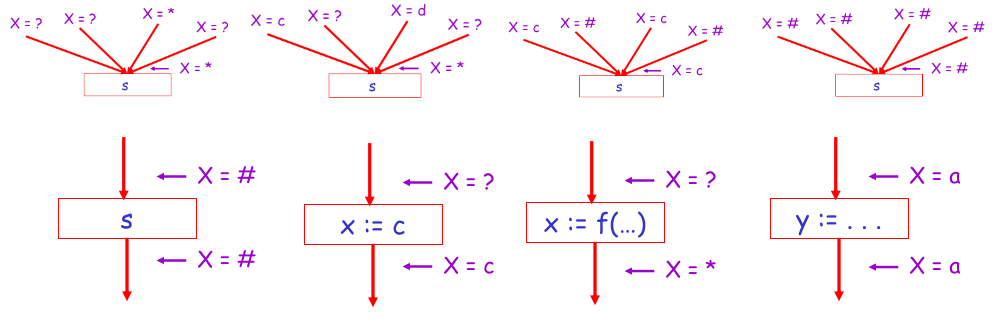
我们有判断常数传播的算法:
一开始每个函数第一个 entry instruction 设置
剩余的指令设置
从前向后检查所有 statements,根据 rule 1-8 修正
例子:
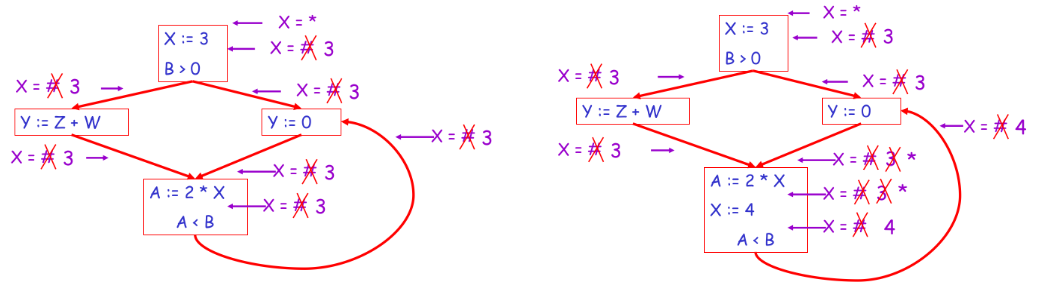
上面的规则不优雅。我们将上面总结的规律进一步形式化,使用偏序关系描述:
那么 rule 1-4 可以被重写为:
其中
我们再分析算法特征,发现每个
最多被修改两次,而且必须是沿着上面偏序关系增大的方向修改。 因此该算法相对于程序大小线性增长。
6.2.3 Summary
如此的全局分析还有很多,只不过我们选取了 liveness check 和 constant propagation 两种全局分析的类型介绍。更多的全局分析和优化可以读者自行实现。
Chapter 7. Register Allocation
7.1 Problem Definitions
我们在经历上述一系列操作后,终于要到了寄存器分配的环节了。在这个阶段完成后,真正可以被汇编器汇编的汇编代码就能生成了,编译器的工作就算告一段落!
我们之前引入的无限寄存器的假设实际上在真正的物理机器上是不能实现的,因此在这个阶段的主要任务是,把全局临时寄存器替换为目标平台的真实物理寄存器,同时还要注意变量的存活情况,不能让两个同时存活的变量(即存活区间重叠的变量)使用同一个物理寄存器。
回顾一下 liveness check 的内容,并且用形式化的方法表达:
对控制流图中的每个结点
并且我们定义两个变量相干(interfere),当且仅当它们俩:
初始状态都是同时存活的,例如刚进入一个函数时,callee-saved registers 都应该认为是存活的(同时存放到一个 callee-saved registers 时就是冲突的)、函数的 return value 中如果同时用到这两个变量也是同时存活的;
在
相干的性质:两个相干变量不能共用一个寄存器。我们在寄存器分配时只需要保证:
两个相干变量不分配到同一寄存器;
并且使用的都是 target machine 的物理寄存器,不够的就 spill;
就能正确地完成寄存器分配的任务了。
我们再定义 控制流图(Control-Flow Graph):控制流图中,每个结点是一条指令,每条边是控制流向。
在冲突分析时,我们需要引入新的图:冲突图(Interference Graph)。冲突图中的结点表示一个变量,冲突图中的边代表所连两个顶点代表的变量是相干的;
很容易知道,控制流图是有向图、冲突图是无向图;
现在,我们想让 “两个相干变量不分配到同一寄存器”,只需要给冲突图上色(相邻的结点不能使用一种颜色、颜色的数量就是目标平台物理寄存器的数量)即可!
7.2 K-Coloring & Approximation
现在考虑这几个问题:
如何找到高效的 k-coloring 算法?
如何在染色的同时尽量避免
mov指令(回想之前的MovInstr就是为了尽量避免寄存器值的来回倒腾);如果没法 k-coloring(k 太小了,对指定代码无解),如何进行 register spilling?
首先,K-coloring 算法是 NP Complete 问题,我们只能找近似解。1879 年的 Kempe's Algorithm 就是一个比较快速的算法。
我们考虑:
找图中所有最多存在
然后从栈中逐一 pop 出结点加回原图,并根据它当前的边的限制情况选取颜色;
如果在 第 1 步中发现所有结点都存在多于
例如在
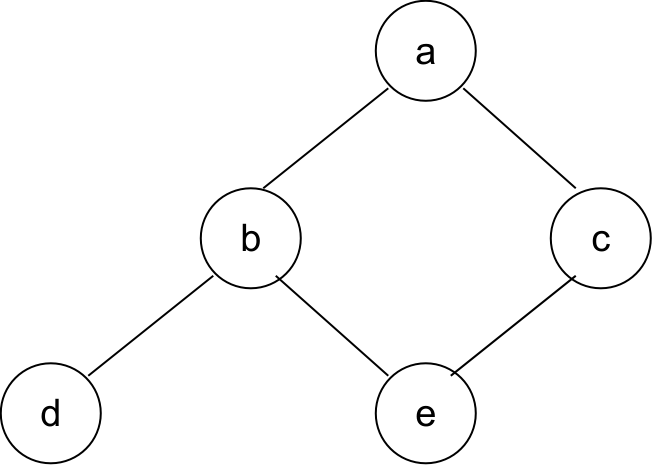
这时我们采取 optimistic coloring policy,认为很少出现 register spilling。于是先把任一个多于
我们发现,实际上
在我们这个近似算法的情况下,可能会进行 register spilling(我们称为 “potential spilling”),步骤如下:
找到仅有 1 条边的
d并将其压栈;发现
a, b, c, e此时正好都有两条边,则任取一个顶点(例如b)和其他重复上述操作,直至所有结点均已压栈,在逐个 pop 到新图、恢复边,并根据依赖上色;
Actual Spilling:如果在弹出栈的时候发现确实没法找到新的满足要求的颜色,这个时候一定需要选择一个结点作为 spilled 结点(可以使用一些 heuristics 方法来获得这个合适的 spill 寄存器);
此时我们假设这个必须 spill 的寄存器为
分配一个栈帧地址
在每次 use
在每次 def
一旦发生了 actual spilling,当前的 coloring strategy 可能就不再是最优的了,我们需要排除
因为 spilling 改变了
因此在重新进行 liveness analysis 时只需要注意更新与
以上的算法已经能解决前面的第一和第三个问题了(已经能够确保程序正确汇编和链接了)。
7.3 Optimization: Register Coalescing
举个例子来演示上述算法:
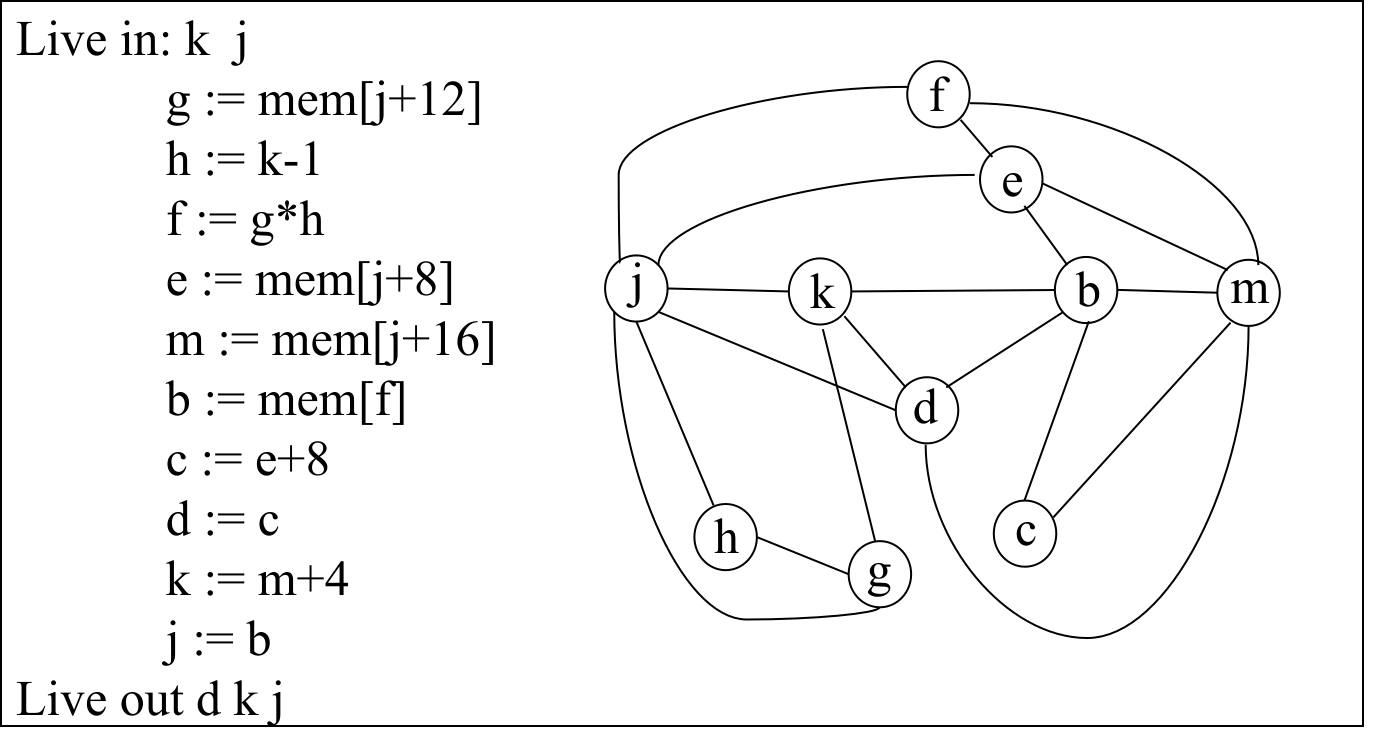
假设上面的代码中,目标平台 k, j 变量在一开始进入时存活、d, k, j 变量在离开时存活,然后整个代码结构如上图所示,我们可以根据 liveness analysis 构建出右边的冲突图。
得到冲突图后,我们再根据上面的算法依次计算,很简单能得到各个染色的方案。
不过我们发现有几点比较灵活:
(前面提到的)在压入栈的时候,没有发现少于
在弹出栈的时候,有些结点能取很多种颜色,我们这里是随机选一个。选哪一个会对最终是否需要 spilling 有影响吗?
在需要 actual spilling 时,使用什么 heuristic 方法选择被 spilled 的寄存器,会对 spilling 的次数有影响吗?
这些问题我们先按下不表。
考虑接下来的情况。我们按照上面的算法会生成一个真正由
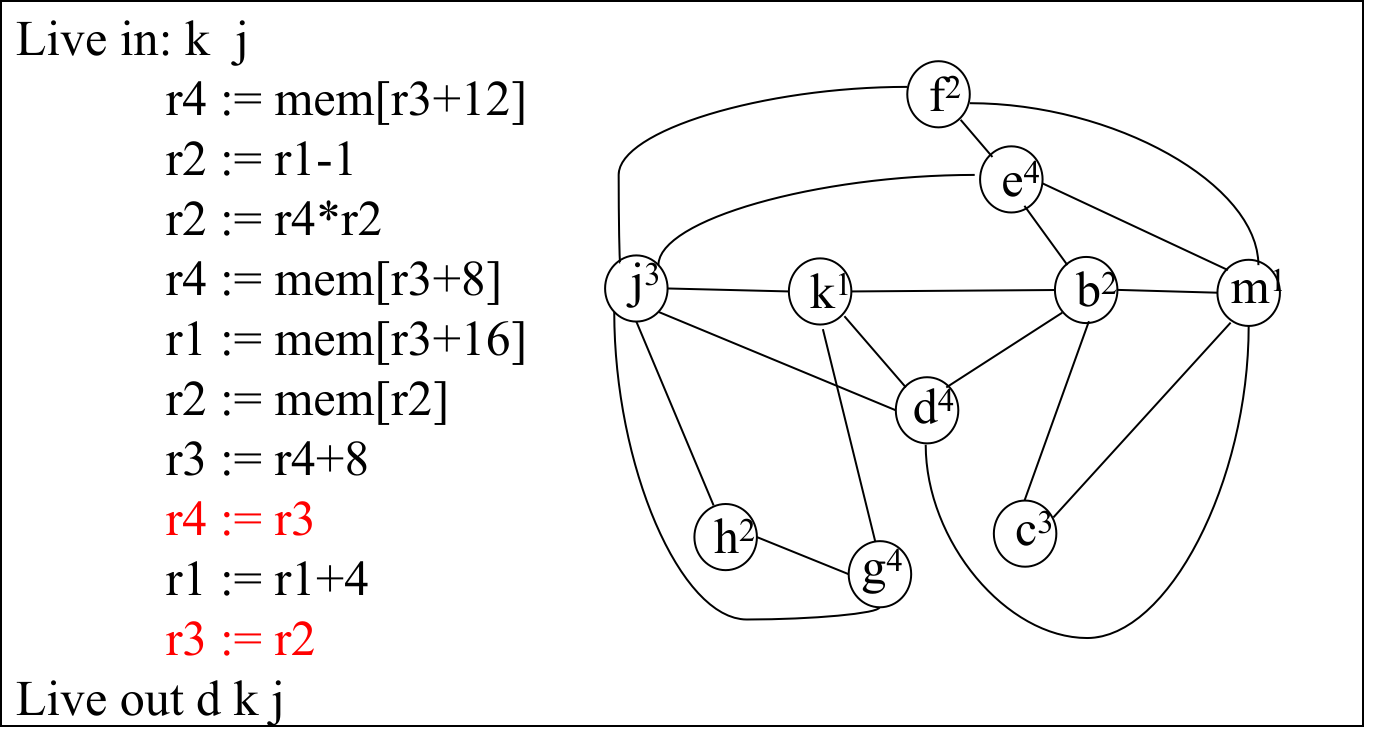
注意到有两步是寄存器间相互转移,是否可以进行优化,避免这种情况(也就是前面的第二个问题,如何在染色的同时尽量避免 mov 指令)?
答案是 coalescing。为了做这个优化,我们需要对冲突图进行改进:
对于所有指令是 Code Generation 阶段生成的 MovInstr(仅寄存器间移动),不妨设为 c -> a,那么在原来算法生成的图中,我们想把 c 和 a 合并,这样可以减少 mov 的次数。但这样的合并不一定正确。因为如果 c 和 a 是相干的呢?所以讨论一下:
如果
a和c没有相干边,则尝试把二者的顶点合并为一个顶点(由于这个想法不能立即得到正确性验证,我们不妨先连一条特殊的边,表示尝试将它们俩合并,我们记作 “合并边”,等到后面再判断能否合并);如果
a和c有相干边:对不起,那肯定是没法合并的,否则根据冲突图的定义必定冲突,因此这两个顶点不能合并;我们将这种 “既满足在
MovInstr的src和dst两端、又满足存在相干性” 的两个变量,它们的 Move 操作称为 “Constrained Move”;例如下图,
x, y和y, z分别各是MovInstr的一组src, dst,我们也许能将x和y合并,但是xy和z即便有合并边,也不能继续合并。因为xy和z本身就是相干的!
为什么 a 和 c 没有相干边的情况下,我们仍然不能直接合并呢?因为合并顶点这个操作可能导致原本可以 k-coloring 的图变成不可被 k-coloring 的图(读者可以自己举一个例子)。于是我们需要在保证 safe 的基础上(不会导致新增 spilling)进行 coalesce。这里有两套 heuristic coalescing strategy:
Briggs' Method(看合并完成之后的情况):如果合并后的结点至少存在
因为在简化其他可以被简化的结点后,该结点的度一定小于
George's Method(看合并之前的情况):
证明:设
如果不进行 coalesce,得到的图为
如果进行 coalesce,得到图
可以证明
也就是说,这样条件下的合并并没有让图变复杂,反而是变简单了、更容易进行染色了。
请再次注意:上述两种策略都有 “两个将合并的点没有相干边” 这个前提!
于是,改进后的 Register Allocation 算法是:
通过 liveness analysis 的结果得到一个冲突图。并且在所有
MovInstr联系的src和dst顶点间加上特殊的边(回忆一下前面的定义,不是相干边,而是表示尝试合并的边,我们称为 “合并边”,方便下面的 coalesce 操作);
Warning
请额外注意,构建冲突图的方法不是只看前面的冲突条件(callee-saved/return + 同时存在 out)就能解决!因为还需要考虑有些情况的 registers 的存活条件会被打断(caller-saved)。
因此构建的算法是,对 Instruction 中的每个
Def的元素如果这个指令是 non-move 的,连接所有
out中的每一个元素;如果这个指令是 move 的,连接所有不是
src-dst的边。最后为src-dst的边加上虚线(合并边,而不是冲突边);
按原先的 k-coloring 算法进行 simplify(移除不多于
将存在合并边的顶点视作不可 simplify 的,以此来最大化 coalesce 的可能;
当所有结点都压栈后,进入第 5 步;
当我们发现无法继续 simplify 的时候,进入第 3 步;
使用上述 coalesce 策略判断能否合并:
如果可以,还需要判断两个顶点间有没有相干边(constrained move),没有表示可以合并。合并一次后,立即回到第 2 步;
如果不可以,并且两个顶点间有相干边,则 freeze 掉这条合并边(放弃 coalesce),立即回到第 2 步;
如果不可以,但也没法 freeze,则进入第 4 步;
这时既不能 simplify,也不能 coalesce,还不能 freeze,我们只能认为 potential spilling,先选一个 register 压栈;
现在所有结点都压栈了,我们逐个弹栈并为结点上色。注意,前面已经合并的结点弹出时需要恢复成合并前的图的结构,但是合并的点上的色是一样的;
如果弹栈时出现 actual spilling,则记住把该变量分配到栈上,并继续弹栈(最终再统一放到栈上,参见第 6 步);
再次强调,actual spilling 是在每次 use 前添加 load、每次 def 后添加 store;
弹栈结束时:
如果所有顶点都成功上色,则寄存器分配结束;
如果在第 5 步中有一些 actual spilling 的寄存器,则将它们放在栈上,重写汇编指令,并且重新构建冲突图,回到第 1 步;
当然,如果是考试的话,可以按照下面的算法:
xxxxxxxxxxprocedure Main() LivenessAnalysis() Build() // Build IG MakeWorkList() while True: if simplifyWorkList != {} then Simplify() else if workListMove != {} then Coalesce() else if freezeWorkList != {} then Freeze() else if spillWorkList != {} then SelectSpill() if simplifyWorkList == {} && workListMove == {} && freezeWorkList == {} && spillWorkList == {} then break AssignColor() if spilledNodes() != {} then RewriteProgram(spilledNodes) Main()
7.4 Misc: Architecture Conventions & Pre-colored Nodes
现在寄存器分配的算法已经完成了,但是还需要考虑某些体系结构的 conventions 的限制,例如某些操作必须使用哪一个寄存器,例如 x86 架构(x86-64 同理):
寄存器内存索引语法,
d(a, b, [1,2,4,8])规定a, b都不能是%esp、a是%ebp的情况下不能没有d,等等;需要遵循固定的 calling conventions(包括参数传递、返回值的寄存器,等等。);
%esp只能用来作为栈指针;div指令会使用%edx:%eax作为 dividend;……
其实我们已经在 code generation 阶段讨论过这些问题了,因为这些有特定规则的寄存器会在 code generation 阶段就确定下来究竟用什么物理寄存器,这样到了 register allocation 阶段,这些结点就变成了预上色的结点(pre-colored nodes)。
除了 conventions,其实我们发现前面的寄存器分配的算法只是告诉我们哪些变量可以分配到同一个寄存器上,没说具体分配到哪个物理寄存器上。
因此,我们直接借助 pre-colored nodes 的抽象,将所有物理寄存器也看作结点,构成一个
注意:如果有些 calling convention 不希望在任何地方分配某个寄存器,例如 x86 下的 %rsp,那么不建议把它加入 Interference Graph(否则没有存活关系的话会被分配走);
为什么这里物理寄存器看成完全图?
因为这里是物理寄存器而不是变量,它们始终是同时 “存活” 的。
并且,所有 pre-colored nodes(不仅是物理寄存器代表的结点)都不能进行 simplify(上述算法 simplify 到只剩 pre-colored nodes 后即可弹栈)、不能进行 spill(不能选 pre-colored nodes 来 spilling 到栈上);
但是其他正常结点是可以 coalesce 到 pre-colored nodes 上的(如果条件允许的话)!
正因为 pre-colored nodes 的 “特权” 问题,导致如果 pre-colored nodes 比较多、持续的生命周期长,就会更容易导致 register spill。
所以我们应该尽量缩短 pre-colored nodes 的存活周期。例如我们在 code generation 时就先把 callee-saved registers 放到全局临时寄存器中,这也是因为这个原因。
同样的道理,在 code generation 阶段解析函数开头时,也会把参数寄存器(如 %rdi, %rsi, ...)先放到临时寄存器(non-escaped)/ 栈(escaped)中,有助于摆脱这些 “写死的物理寄存器长期存活” 的问题。
这样在寄存器使用紧张时可以更合理地将某些寄存器推到栈上,寄存器使用不紧张时又可以避免
mov,相较于这些 pre-colored nodes 一直霸占这些物理寄存器的方案而言,后者可以产出更优的分配方案。
另外,需要补充的一点是,对于 non-precolored nodes,判断是否 coalesce 建议使用 Briggs' Method,对于 precolored nodes,判断是否 coalesce 建议使用 Geroge's Method;
这么做是一方面为了答题解法的唯一性(不然简化的思路就有多种了);
另一方面是可能没有必要。例如对于 non-precolored nodes,如果用 Geroge's Method 判断,可能合并后的结点度数还是大于
,没法继续进行,因此不适合在只有 non-precolored nodes 的情况下使用;
7.5 Corner Case: Caller Registers
前面我们讨论完了在一个函数内部的正常的寄存器分配的流程。现在我们关注一些边界情况。
在一个函数内部的 call 指令会改变前后的寄存器 liveness 的状态吗?答案是会。根据 x86 架构的 calling conventions,我们可以认为进行一次 call 指令后相当于对所有的 caller-saved register 进行了一次 def(也就是表示调用函数前需要保证 caller-saved registers 不能是存活的)。
7.6 Put it Together: A Complete Example
现在,我们看看如何从头到尾地完整看一遍寄存器分配的算法及其优化策略。
假设某目标平台有 3 个物理寄存器
以下面的程序为例:
xxxxxxxxxxint f(int a, int b) { int d = 0; int e = a; do { d = d + b; e = e - 1; } while (e > 0); return d;}它翻译成的汇编的形式含义如下:
xxxxxxxxxxenter: c <- r3 (callee-saved) a <- r1 b <- r2 d <- 0 e <- aloop: d <- d + b e <- e - 1 if e > 0 goto loop r1 <- d r3 <- c return (r1, r3) live-out于是我们根据 liveness analysis 可以绘制出冲突图:
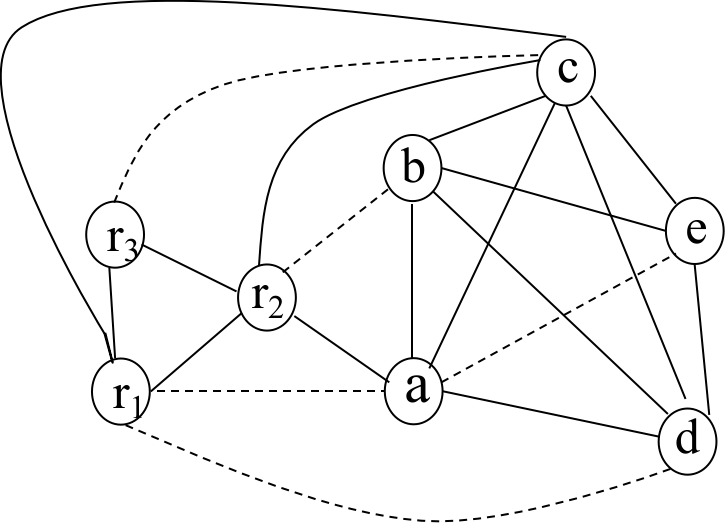
注意到,一开始无法进行任何的 simplify,因此考虑 coalesce;我们发现任何企图 coalesce 的操作都会生成一个不少于
还记得我们在 7.3 节提出的 3 个问题吗?其中一个问题说 “在压入栈的时候,没有发现少于
这里我们综合考量循环内外该变量 Use+Def 次数(循环内外分开考虑是因为调用次数有很大差距,需要加权),以及该结点在冲突图中的度(度越大说明把它放到栈上后,其他的结点更不容易出现 spilled)。我们的计算公式如下:
注意 inside loop 平均的执行次数是 outside loop 的 10 倍;
假设计算出 c 的 priority 值最小,则选择它来 potential spill;
此时仍然不能 simplify,我们使用 Briggs' Method 发现可以将 a, e 进行 coalesce,并且依此类推:

最终剩余 d 时,注意到可以 Simplify,因此将 d 压栈;然后压栈完成,我们弹出栈顶的 d 并为它分配颜色(显然是和 r3 相同);
注意,在 coalesce 到物理寄存器的时候,我们已经能确定
a, e, b的颜色了;
再弹出 c 时发现确实没有更多的颜色能指派了,因此变成了 actual spilling,我们需要重写原来的程序,把 c 放到栈上:
xxxxxxxxxxenter: c1 <- r3 (callee-saved) M[c_loc] <- c1 a <- r1 b <- r2 d <- 0 e <- aloop: d <- d + b e <- e - 1 if e > 0 goto loop r1 <- d c2 <- M[c_loc] # 注意:由于 SSA,每一次取回 c 的寄存器应该分配新的临时寄存器! r3 <- c2 return (r1, r3) live-out重复上面的 liveness analysis、构建 IG 的过程:

7.7 Too Many Spilling Registers?
当 spilling registers 很多的时候,免不了会有两个 spilling register 间相互移动的指令的情况,这个时候会被翻译成两个内存的 load + store 操作,时间开销比较大;为了缓解这个问题,我们可以对 spilled registers 做同样的 coalesce 操作(即为 spilling registers 单独构建冲突图、染色,颜色就是 InFrameAccess(x),不过由于内存可用的极大,因此认为有无限种颜色),减少这样 spilling registers 间的移动指令;
7.8 R.A. Implementation in Tiger Compiler
首先无论是控制流图还是冲突图,都需要用图数据结构描述。我们讨论一下图数据结构的接口:
Node类型:Degree()度数、NodeInfo()结点相关信息、Pred() / Succ()结点的前后继;Graph类型:NewNode(x)创建新结点、NewEdge(n, m)创建n -> m的边(边没有单独的数据结构,只是更新n的后继、m的前驱,更新m的邻接为 前驱和后继的并集);x中存放的是不同图结点的信息,例如 CFG 结点放的是指令、IG 结点存放的是变量(temp::Temp全局临时寄存器);除了这种方法能存放信息,还可以利用
graph::Table来存放结点到自定义的数据间的映射关系。FlowGraphFactory类型:xxxxxxxxxxclass FlowGraphFactory {public:// 根据给定的 instr_list_ 构建 flowgraph_,每个 Instr 会对应生成一个结点,Instr 的 jump 域会被作为创建 CFG 边的依据void AssemFlowGraph();graph::Graph<assem::Instr> *GetFlowGraph() { return flowgraph_; }private:assem::InstrList *instr_list_;graph::Graph<assem::Instr> *flowgraph_;// 记录构建过程中 labels 和 nodes 间的联系tab::Table<temp::Label, graph::Node<assem::Instr>> *label_map_;};
然后我们看 liveness analysis 的实现的辅助数据结构:tab::Table<graph::Node<assem::Instr>, temp::TempList>>,我们可以用这个表来记录 CFG 结点前后的 liveness 情况(记录 Instr 对应的 Node 开始前和结束后存活的寄存器有哪些;
此外,我们还需要构建一个 live::LiveGraph(冲突图)从之前的 liveness 信息中构建出一个各变量间的冲突图;
以及一个表示 MovInstr 对应的合并边的表(node-pairs);
为了方便起见,我们还可以使用 temp::Map 来存放 precolored nodes 的映射;
另外在算法实现的层面考虑,由于图着色算法需要频繁查看冲突图数据结构:
获得与结点
判断
如果以邻接表的形式存放冲突图,则对第一种调用更快,如果以邻接矩阵的形式存放冲突图,则对第二种调用更快;因此我们一般用邻接表 + 邻接矩阵的方式共同表示冲突图,并且由于物理寄存器结点间存在团,边相当很多,因此不将物理寄存器表示在邻接表中(更何况 Geroge 判断临时寄存器能否 coalesce 到物理寄存器时不需要物理寄存器的邻接表)。
Chapter 8. Garbage Collection (GC)
8.1 Problem Definition
8.1.1 Why & How
通常情况下,无论是什么语言,在运行时想要分配空间,要么放在栈上、要么放在堆上。
栈上分配的变量全权由编译器管理,我们在之前已经做过了(回想一下令人讨厌的 global frame size),这也是绝大多数语言的(解释型语言则是解释器)共性;
但是部分语言的有一部分空间是分配在堆上的。例如 tiger 语言中,我们初始化数组/结构体,它调用的 runtime function 底层由 C++ 实现,最终就是分配在堆上的。
如果这类使用堆空间的语言,在运行时不及时释放堆空间,可能会导致堆溢出的问题。由于像 tiger 这样的语言不涉及底层的结构(包括 Python、Java 等等),没有指针的概念,自然也没办法自己释放,或者这种语言的定位就是不需要开发者来释放(所谓 “内存安全”),那么还需要借助运行时机制来管理堆空间。
垃圾回收的基本原理就是,当一个被分配的地址没办法被当前的任何指针/变量访问到(not reachable),那么就需要运行时工具帮助释放这片空间,使得它能够被重新分配和使用。
更准确一点,其实应该进行 liveness analysis(就像前面设计编译器时做的),但是运行时显然不方便做这种静态分析(运行时难以看出)。因此人们通常使用可达性(reachability)来代替 liveness 进行分析,只不过 reachability 可能没有 liveness 那么及时 / 精确(还可能出现一些问题,后面讨论)。
也就是说,如果存活,一定可达(这是由各个语言的编译器保证的)。
于是,垃圾回收的过程就是,从当前已知存活的变量开始(例如当前栈帧上、寄存器中正在使用的变量),递归地去搜索可达的内存区域,再把分配过、但不可达的内存释放即可。
我们通常使用有向图去描述 “两个存活变量间的可达关系”:结点表示程序当前栈上/寄存器中正在使用的变量 和 堆上分配的记录,边表示地址指针;
所以,几乎所有自动 GC 都遵循一个理念:按照某个策略预定的时间(定时策略),释放不再继续使用的(标记策略)引用类型变量所占用的空间;
为什么加上了 “定时”:运行时是动态的,总不能只回收一次,或者一直回收;
8.1.2 GC Metrics
另外还有一点需要注意的是,GC 通常会伴随一段时间的 STW(stop-the-world,时停),此时段间,无论这个语言是单线程还是多线程的,都需要全部暂停等待 GC 的处理。
这样的 STW 在大多数 GC 算法中都是必要的,不过有长有短(取决于具体算法)。这主要是因为 GC 在运行时总有一些数据需要确保 synchronization,防止并发的回收造成数据不安全的问题。我将 STW 的时长称为 GC 算法的时延(GC latency);
还有一点需要明确的是,我们引入 GC 是为了防止内存泄漏。而 “内存泄漏” 这个概念本身并不是说没有回收完所有的不再使用的空间就是泄漏了,而是没有及时的回收不再使用的堆空间,引发的一系列问题,包括堆溢出。
所以重点在于 “及时” 而不是 “全部”。也就是说,一个 GC 算法可以不需要在一次回收过程清理掉全部的垃圾,而是只需要确保及时就行。
于是我们还可以定义 GC throughput,即一次 GC 操作中,单位时间内回收记录的数量,这个指标能间接反映这个 GC 算法的效率,以及它究竟是否 “及时”。
8.2 Mark & Swap
一种 GC 策略是 “标记清除”(Mark-And-Swap,标记策略)+ 溢出清理(定时策略):
Mark:从可达有向图的根结点(已知存活的变量)开始遍历,将遇到的所有结点全部标记一遍;
Swap:将整个堆扫描一遍,把没有标记的结点放到 free list 中(相当于释放),并且清空所有标记(为下一轮 GC 准备);
程序在 GC 开始时 freeze,在 GC 结束时 resume,从 free list 中分配堆空间;
程序只有在 free list 为空时才进行 GC;
目前正在使用这个策略的语言有 JavaScript;
xxxxxxxxxxMark phase: for each root v DFS(v)
Sweep phase: p <- first address in heap while p < last address in heap if record p is marked unmark p else let f1 be the first field in p p.f1 <- freelist freelist <- p p <- p + (size of record p)
function DFS(x) if x is a pointer and points to record y if record y is not marked mark y for each field fi of record y DFS(y.fi)这样做的优缺点:
优点:算法简单便于实现,很多情况下确实是有效的(满了就回收全部的垃圾);
缺点:性能不佳(扫描全堆,throughput 不大),而且需要经常打断程序执行流先做垃圾回收,程序效率不佳(总体 STW 很长)。
分析一下:
于是我们知道:当
第二个改进,是考虑到如果只使用 DFS 函数调用递归很可能导致栈溢出(因为堆本身是很大的),考虑引入 显式的栈来实现 DFS;
更有技巧一点的话,我们在单线程的 GC 中还能只用每个结点中的空闲数据实现一个不用栈的版本(但是算法复杂、实现的也很少):

这个算法简言之,就是让 y.f0(原来存放的是指针指向的 record)始终存放 GC 的处理指针(x)上一步经过的 record 的地址(因此得名 pointer reversal),方便退出递归时原路返回;
图中 record 前面的 0/1 这样的数字表示 done[i],不仅有索引 fields 的作用,还起到了标记这个 record 是否被访问过的作用。
第三个改进,对于 free list,我们可以模仿 Memory Allocation 的 aggregation list,管理多个 free list 并按照列表的大小来分类;
8.3 Reference Count
还有一类常见的 GC 策略是 “引用计数”(标记策略)+ 分配时清理(定时策略);
目前使用这种 GC 策略的语言有 Python、Swift 等等;
这里我们对每一个在堆上的 record 维护一个额外的字段(ref_cnt)表明当前有多少变量指向它。
然后在赋值、作用域变化等等情况时更新变量对应的值就行。
举个例子,例如 record
x的某个 fieldx.fi原本是z(是堆上的 record)赋值为y(另一个堆上的 record)此时:
读写
y的 reference count 使其增加;读写
z的 reference count 使其减少;检查
z的 reference count 如果是 0,则将z加入 freelist;而
z中的字段(例如z.fi)如果是堆上的指针,则推迟到z所在的地址被从 free list 分配出去时再减小 reference count;
于是相较于同步的 Mark-and-Swap,引用计数的好处是:
避免了批量、递归的检查回收操作,将部分的更新引用计数操作推迟到分配时(批处理提升了 GC throughput);
不需要频繁进行全堆扫描,提升了程序执行效率(压缩了 STW 的时长);
只不过引用计数还引入了一些问题:
循环引用:相互引用的变量无法让
ref_cnt减为 0(信息不充分会导致回收不充分);解决方法 1:引入语义层面的语法特性,例如弱引用(Weak References),当内存压力比较大的时候,将这种弱引用视为没有引用。
但是这相当于把难题丢给了开发者,容易导致程序运行时错误的出现(例如使用一个被释放了的弱引用变量);
解决方法 2:进行简单的 cycle detection,对某些容易成环的地方进行特殊检查,及时除环;
解决方法 3:与 mark & swap 结合(occasional),补上全局信息,但 mark 操作很昂贵;
内存访问性能问题:例如
x.fi <- p这个语句在加上引用计数的 GC 后,会变成 3 次内存访问,性能可能更差些:xxxxxxxxxxz <- x.fic <- z.countc <- c – 1z.count <- cif c = 0 call putOnFreelistx.fi <- pc <- p.countc <- c + 1p.count <- c
正因为这两个问题,我们常常在一些 GC 学术原型中才能见到它,实际使用这种方法会出现一些难以避免的性能问题。但是不可否认的是,这种方法(思路)真的很简单和显然,所以它也被常常应用到其他的领域和方面。例如 file table 维护文件打开状态时使用、虚拟页和物理页的映射时物理页维护引用计数、C++ 的智能指针 shared_ptr 等等。
8.4 Copy Collection
这类 GC 策略比较新,有些现代的应用(例如 Android 10+)就在使用这种 GC 策略。内容如下:
将 heap 拆成两个部分:from-space & to-space;
from-space 专门存放分配的内容,to-space 专门管理回收的内容;
两个 space 都有一个
limit指针表示该区域结尾;next表示该区域接下来要插入的位置,分配内存就是向next后面追加可达的 entry;如果
next到limit的位置,证明当前的 semi-space 满了,我们从root根结点(目前肯定存活的)开始,将所有可达结点 copy 到另一个 semi-space 中(next也移过去了),相当于丢弃了不可达结点、变相进行了一次 GC;
这样做有几点好处:
不需要特地进行 mark + sweep 了,操作更简单,降低了时间复杂度,一次 copy 足矣(进一步降低 STW 长度);
每次 copy 都相当于整理出了连续的空闲堆空间,方便分配、减小了 external fragments,最大化 memory utilization;
相比于 mark-and-sweep 也有坏处:
如果大部分变量存活时间很长(
一半的空间利用率低下;
实现 Copy Collection 的算法是 Cheney’s algorithm:
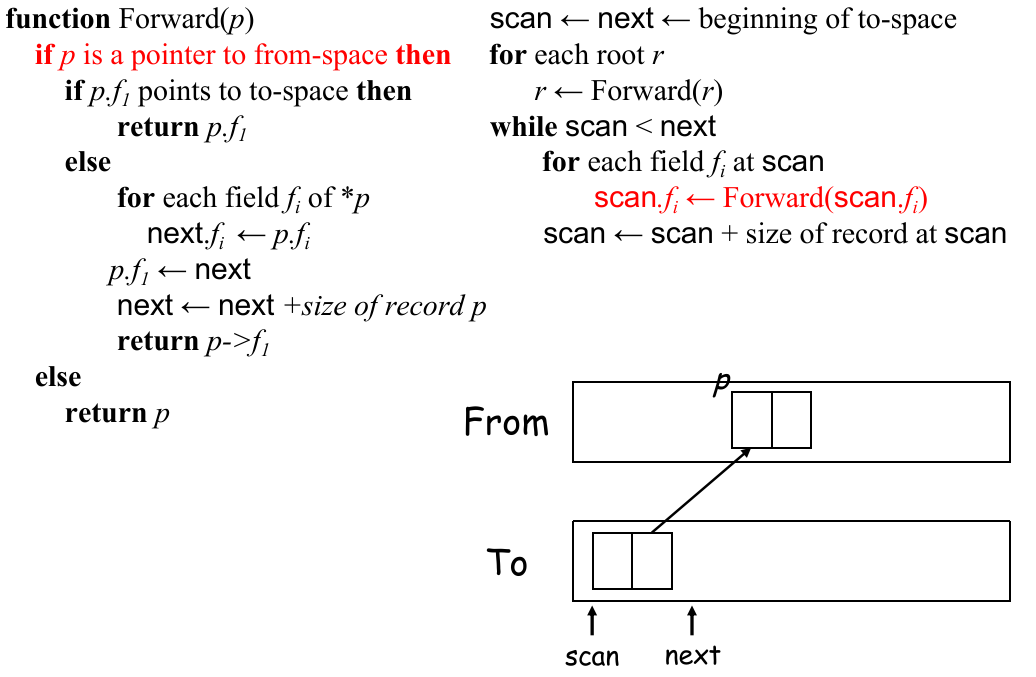
解释一下算法:
把当前准备切走的一边称为 from-space,另一边称为 to-space;
每个被分配的 entry(
)的第一个字段( )保存指向当前分配对象自己的指针(只有在移动更新时指向新的对应的 entry),其他字段( )存放正常被分配的数据;
Forward(p)函数的含义是将p指针对应的结点数据完全移动到 to-space(如果已经完成移动则什么也不做);主函数的算法就是从根结点开始(先 forward 根结点)BFS 遍历结点、更新
scan,遍历到的直接调用Forward转移。同时需要更新拿在手上的指针,保证上层应用无感;
这种算法有些优缺点:
优点:不引入额外数据结构(没有额外的栈、不需要 reversal pointers);
缺点:影响原来程序的 locality!无法充分利用局部性(不相干的 record 可能被复制到一起),这会降低每次 GC 后的程序执行效率;
因此我们作出优化:Semi-depth-first Algorithm,这也是 Copy Collection 最常见的实现方法:

这个算法的思路是 DFS,所以主函数省略了(就是对每个 root 结点调用 Forward 然后结束)。这个 Forward 函数我们在 Cheney's Algorithm 中见过类似的结构,就是如果当前 entry(由 p 指向)完全移到 to-space(第一字段已经在 to-space 了),那么就直接返回,否则调用 chase 迁移;
主要看 Chase(p) 的做法。q 和 next 有点像算法里的左右指针,q 表示当前正在迁移的 entry 的开头,next 则表示正在迁移的 entry 的结尾;
而 r 和 p 又像一对前后指针,p 表示当前正在 copy 的节点,r 则是一轮 semi-DFS 从根到叶遍历的指针;
中间 for 循环的作用是把要 copy 的 p 指向的 entry 的每个字段都复制到 to-space 中。同时 Chase 还需要考虑 p entry 中指向 from-space(分配在堆上但没迁移的 entry)的指针。
为什么
Chase需要考虑p中的指向 from-space 的指针?因为这里是 DFS,不能直接结束对p的迁移,否则就变成 BFS 了(Cheney's Algorithm);应该像这样一直沿树边递归到底;
一轮 semi-DFS 后,如果 p 有多个 field 都指向堆,那么默认是先 copy 当前 p entry 中的最后一个 from-space 分配的地址,方便 repeat 循环递归(DFS)地移动 from-space 中分配的 entries;
为啥是 copy 最后一个?因为递归过程一次只能保存一个,这也是算法称为 “semi-DFS” 的原因(没有完全遵循 DFS 的遍历方法)。更清楚一点,我们可以看下面的比较图(注意到 4、6 是最后才访问的):
例如
1 -> 2 -> 5后,一轮 semi-DFS 结束,虽然看到了4对应的 record,但也只是更新了2的 record 的指针,并没有 copy4的 record 到 to-space;随后递归回溯到1再继续;
Optimizations?
注意到,copy collection 对于堆空间的浪费还是很严重的,因为每次只使用一半的堆空间(另一边必须是无效的)。于是一个很简单的优化是,底层使用 mmap 来处理对堆空间的分配。我们可以让另一半(不在使用的 to-space)在 copy 前是 unmap 的状态(未分配物理页),这样能更充分地利用机器资源。
但这么做也有点问题,在 GC collector 进行 copy collection 的途中可能出现物理内存猛增的情况;
但这确实能缓解在除了 GC 阶段以外的其他时间里内存不够用的情况。
注意到 Copy Collection 的均摊开销主要在
8.5 General Collection (Generations)
8.5.1 Design
一般情况下,GC 的 throughput 和 latency 是相互制约的,例如我想要确保 throughput 很大,一般需要扫描更多的信息来进行批处理,但扫描更多的信息会导致 latency 的延长。
但是这种 GC 的策略相较于前面几种方法,可以同时提升 throughput、降低 latency。主要是人们有以下的特性的观察(不是准确和普适的定律,而是经验假设):
堆上新创建的对象通常更容易先死去;
堆上存活的时间越长的对象通常更不容易死去;
堆上存活时间长的越长,短的越可能更短。也许可以用马太效应解释;
基于这个特性,人们提出了 general collection 的 GC 策略(分代):
将 heap 分为若干区域
GC collector 重点回收
其实
相反的情况,如果
每次
这样做带来的好处是,每次回收只需要扫描原先 20% 左右的区域,但是能回收率能达到 80%,不仅减小了 latency(扫描的区域少了),而且增大了 throughput(单位时间回收的量增多了),极大提升 GC 效率。
这种策略的均摊时间开销:
可是,如果涉及更旧代的回收,时间开销还是很大的(例如如果只有两代,并且做一次
8.5.2 Patch: Ways of Remembering
现在回过头看一下,如果使用 general collection,有个问题是我们 “同时需要关注
虽然就像前面说的,这种情况很罕见,但还是需要考虑的,例如堆上分配的结构体在它被分配的很久以后突然更新了一个字段,这种情况就可能出现上述罕见的现象。于是我们需要单独保存一些旧代中有指针指向新代的信息(不然 GC collector 很难判断
为了解决这个问题,人们首先想出了借助一个 Remembered List 的方法:每次更新被分配 entry 的某个字段时,向这个 list 中加入一条更新的记录。这种方法有个问题,就是实际上可用的堆的空间一般很大,平均需要记录的更新数据可能会达到数个 MB,这对于一个内存中的列表而言开销已经比较大了。
于是人们想使用 Remembered Set 来存放,因为它的去重性质,我们可以在分配的 object
以上两种方法的粒度都是对象(很细),免不了占用比较大的内存资源。
于是人们提出了粗粒度的信息存放方案(Card Marking,比较主流的实现方案):
将内存分为
一个对象可以占据一个卡片的一部分,或者从卡片中间区域开始占据到后面的卡片;
当
可以用更小的 list(byte index 向右移动了
具体实现就是在每次更新 object 时打桩(在 obj.f = a 的后面加上代码,判断如果确实是 G1 指向 G0 的情况,则从 card 对应的 list 中取出并更新);
坏处:不清楚在这片区域的 cross generation pointer 具体在哪里,还需要在这片区域内继续查找(空间换时间);
另一种方法是用 Page 的粒度来管理这个信息(Page Marking):
就像 card marking,不过
更新一个分配的 object 相当于 makes the page dirty;
用户态程序可以在每次 GC 后标记 write-protected;
这样相当于把 card marking 的打桩操作变成了用户态的 fault handler。但实际上开销也不小(毕竟需要进出内核以及用户态 handler);
8.6 Incremental Collection
这里还有个更加复杂的回收策略,和实际应用结合得比较紧密。
这个策略着重关注于优化 STW 时长(latency)这个指标,希望 GC 让应用停止的时间尽可能短(尤其是在涉及 UI 前台类型/端侧的语言中,不希望用户感受到卡顿);
比如对于数十 GB 的内存而言,同步的 Mark & Swap 的 STW 可能在百毫秒级别,这对后台程序 / 服务器应用而言不那么关心,但是如果是端侧设备 / 浏览器 / 游戏设备 / 精确的嵌入式设备呢?这个问题就很突出了。
这个时候,两种思路:
让 GC 回收程序和应用并发执行(从根本上极大缩短甚至基本消灭 STW);
让 GC 回收程序按应用执行的情况增量地回收(通过减少需要扫描的数据量,也能极大缩短 STW);
这时我们需要引入一些概念:
Collector:专门收集不再使用的分配的空间并释放;
Mutator:改变 reachable data 的关联图;
将应用中改变 reachable 关系的逻辑抽象出来,它就是之前阻碍 GC collector 并发,也是 STW 出现的主要原因;
Incremental Collection:只有 Mutator 需要 Collector 回收时才进行回收(调用式关系);
Concurrent Collection:在 Mutator 执行期间 Collector 并发执行(后台服务关系);
现在介绍一种 Incremental Collection 的实现模型:Tricolor Marking(三色标记模型);
任意一个被分配的记录只会处于 3 种颜色中:
White: not visited by GC;
Grey: visited by GC, but its children are not;
Black: visited by GC, so as its children;
算法如下:
xxxxxxxxxxprocedure tricolor-marking:set root object gray // visit
while they are any gray objects: select a gray record p for each field fi of p: if fi.p is white: color fi.p gray // visit first time (可以用栈压入来实现) color record p black // visit second time (可以用栈弹出来实现)这里是 BFS 性质的遍历所以使用栈数据结构。可以类比,Copy Collection 中的 Cheney's Algorithm,可以使用队列数据结构来实现;
这里注意几个算法不变量(Invariants),它们是构建 Incremental Collection 的根本原理:
不存在黑结点直接指向白结点的情况。如果有就说明黑色结点对应的对象并没有处理完全,出现了数据不一致的问题;
灰结点一定在 collector 的数据结构(fringe)中,意味着正在处理;
现在,我们希望在 tricolor marking 的基础上引入 incremental collection,就意味着,被分配的 object 在 GC 结束后继续留有标记,交给 mutator 执行。
过一段时间后,再次进入 GC 执行算法时,可能就会出现上述算法不变量的违反。
例如,已经染黑的结点(GC 完全扫描的结点)在上一轮 GC 结束后,被 mutator 追加了白色结点(上一轮 GC 结束后才分配的),这个时候就违反了第一个 invariant。
于是!所谓的 incremental collection 做增量回收,就是通过在 runtime 分配堆空间时,采取措施保证 invariants 的成立(在 mutator 运行时,而非 collector 运行时),对变化的部分进行 GC 检查。
基本的思路还是,针对基本的读写操作进行打桩(barriers):
Method 1 (Dijkstra, Lamport):向黑结点 object 写入指针 field (插入白结点)时染灰(纳入 GC 管理中);
Method 2 (Steele):向黑结点 object 写入指针 field (插入白结点)时将父黑结点染灰(dirty,让之前的结点重新放入 GC fringe、表示需要重新扫描);
(Boehm, Demers, Shenker) 改进是把 black 结点的页改成 write-protected,page fault handler 更改权限为 writable,并且标记为灰色(但这么做也有性能问题);
Method 3 (Baker):在读灰结点 object 的白子结点时提前将该白结点染灰(纳入 GC 管理),这样 mutator 永远无法获得一个不受 GC 管理的指针了!因此就不会出现 invariant 的违反问题;
(Appel, Ellis, Li) 改进还是利用 page fault,但这个时候直接从灰结点开始进行一次 GC,染成黑色-灰色的结点;
于是,我们基于 Copy Collection 的 Cheney's Algorithm 实现一个 Incremental Collection 算法 (read):Baker's Algorithm;
基本前提:应用(mutator)和 GC(collector)处于同一线程中;
定时策略:仅 allocate memory 时交互进行;
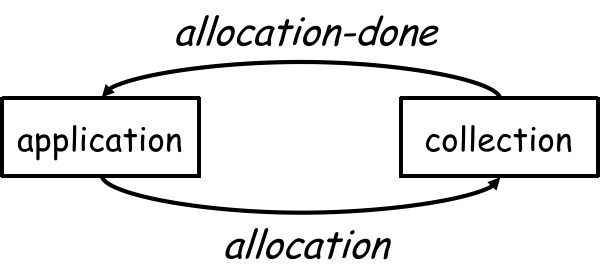
仍然把 heap 分为 from-space 和 to-space 两个部分;
GC 过程仍然从堆内存满了后开始,但不是一次性做完,而是每次 allocation 时增量地做一点;步骤如下:
当堆(from-space)满后,交换二者角色,现在 from-space 变成空的一边;并且立即 forward root 结点到 from-space;

第一步结束后,不继续复制,而是先退出 GC 例程,回到应用(有点像协程 coroutine);当应用在 GC 例程暂停期间 allocate 堆时,会再次唤醒 GC,此时:
会直接分配在空的 from-space 的末端(减小 limit 的指针位置);
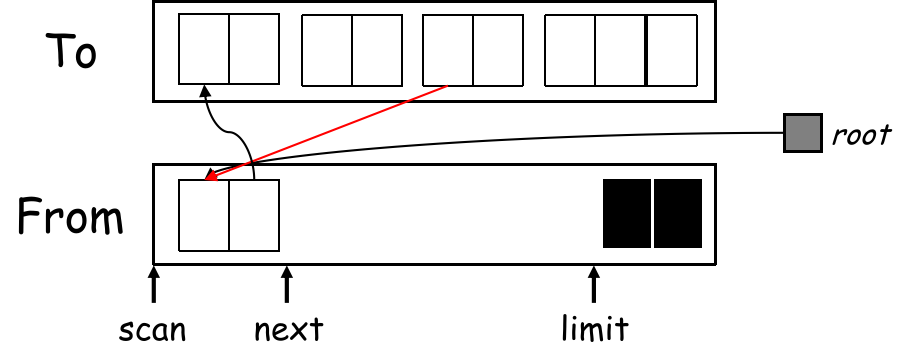
对应的扫描并从 to-space 中复制已分配记录(注意,如果分配了 N bytes 空间,那么从 to-space 扫描的大小不小于 N bytes,为了 copy 的过程不慢于应用分配的速度)。注意 forwarding pointers;
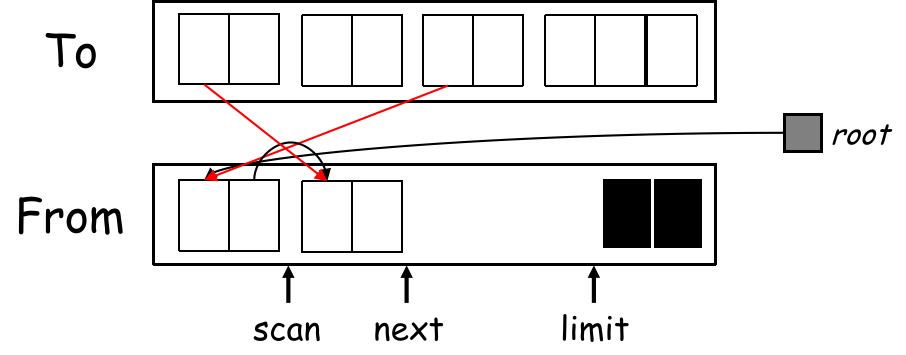
第一步结束后,如果应用在 GC 例程暂停期间 load references,创建了指向 to-space entry(这个 entry 是没有被复制到 from-space 过的)的 root 结点,那么根据 tricolor marking 理论,此时 to-space 中未被复制到 from-space 的 entries 全是白结点(没有被 GC 遍历过),这相当于直接将黑结点指向白结点(违反 invariant 1)。我们立即做一次 forward(但不关心它内部的 forwarding pointers):
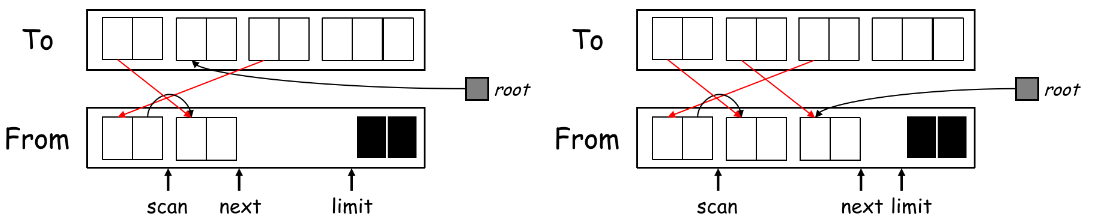
如果指向的 to-space entry 是已被复制的,那么立即 forward:
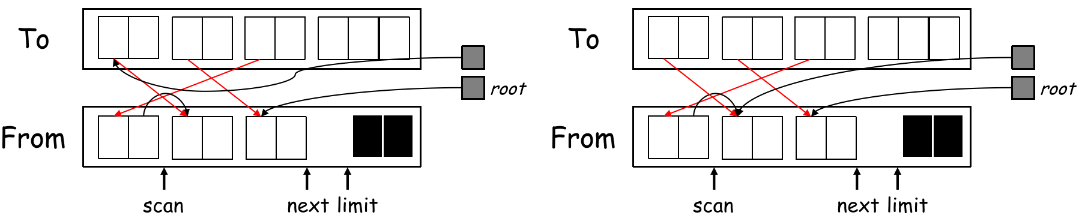
当
scan碰上next时,allocation 结束,本轮 GC 再次暂停,控制权又回到应用;只要保证
总结一下 incremental collection 的优缺点:
优点:时延低,把复制的操作均摊到每次 allocation 时,减小了单次的 STW 时长,对 real-time app 友好;
缺点:总体开销很大,每次 read 都多两条指令(compare & jump);性能开销高出 20%(而且还没有考虑 locality);
8.7 Concurrent Collection
之前我们讨论的是同步 GC,有没有异步 GC 呢?有的。就像前面说的,无论如何都需要 STW 来同步信息,只不过 STW 的长短罢了。在并行 GC 中,STW 的大部分工作都在 synchronization 中;
8.8 GC Interface in Compiler
一个编译器要支持 GC,需要做哪些事情?
record allocation codes(底层为语言 allocate,我们在 translate 阶段做过);
data layout of records(编译器在 allocate records 时分配的数据格式);
编译器需要描述 GC 中的 root(最难,因为 Compiler 静态扫描,需要知道栈上、寄存器中哪些变量是 heap 的 reference、哪些是 literals,而且不能漏,否则有严重问题);
读写打桩(取决于具体 GC 算法);
以 copy collection 为例,为了支持 GC,我们在编译器 allocate records 时需要:
Call the allocate function (allocateRecord);
Test next + N < limit? (test succeeds);
Move next into result;
Move result (next) into some useful place (Can be fetched outside allocation).
Clear M[next], M[next + 1], …, M[next+N-1];
优化:也可以不需要,Store useful values into the record (metadata),但要注意安全问题;
next <- next + N;
Return from the allocate function
call & return 可以 inline 优化;
因此总体而言 allocate record 大约在 4 个 instructions 左右。想进一步优化,则可以考虑将 allocate A 和 allocate B 合并为 allocate A+B(batch);
我们已经完成了 record allocation codes,先从 data layout of records 开始。我们想写一个 GC 扫描 compiler 分配的数据结构,就需要留一个专门的信息来描述这个 data layout;
主要是让
Forward判断哪些是指针,只有是指针的需要递归地 / 放入队列地进行处理;
一种非常简单的解决方案就是在 record 前面加一个 data header(descriptor/type pointer),很多面向对象的语言都是这么解决的(例如 Python type、Java 反射等等,但它们被创建出来还有其他用途);
在 tiger 中,我们可以使用 string 来作为 descriptor,指向
.data区域,每个 field 对应 string 数据中的 1/0(1 是 pointer,0 相反);如果是 array 的话,使用这种方法似乎有些不必要(列表 100 项,字符串长就 100?)
再来看最难的部分,如何描述 GC 中的 root(栈上、寄存器中哪些变量是 heap 的 reference/pointer)?
最简单的方式是猜测!扫描所有 registers 和 stack,数据段中有些数据如果像地址(是否位于 VA 区间、是否对齐有效,等等,也有优化方法)。问题是有些 integer literal 被当成指针,因为猜测总是不准确的(并且还有可能是死亡后的变量留下的)。
这个猜测的做法被称为 approximate GC;
如何做 exact GC?这就需要借助 Compiler 了。因为 compiler 在编译阶段知道哪些栈上/寄存器变量是指针。因此需要编译器和 GC collector 协作才能补全缺失的信息(这个信息在编译后丢失了)。一种解决方案是 compiler 生成一个 pointer map。其中应该包含:
Pointers on stack;
Pointers in callee-saved registers;
GC threads use those pointers to traverse;
那么何时应该创建一个 pointer map?取决于 GC 何时被触发。像 incremental collection,触发时间就是 alloc_record 被调用的时候。因此我们需要在每次函数调用(每次 call)前,生成一次当前 stack + callee-saved registers 的 pointer map 的情况,以便之后调用分配时使用。
我们需要从生成 AST 的 type 时就要准备传递这些类型,
如何存放这个 pointer map?可以放在 .data 段(因为在编译阶段就能确定),用链表进行组织,然后使用 function label 来索引。
pointer map 的内部结构如何设计?对于 stack variables,我们可以记录相对于 stack frame pointer 的值;对于 registers,一种原始的方法是调用前直接将 callee-saved registers push 到栈上,然后 map 中存放的是相对于栈的位置即可(转换成 stack 的情况);
对于 registers 的另一种方法是,可以在 map 中保存一个 bitmap 专门表示 register 是不是 pointer。但问题是 map 中没有实际的值(只有“是否”的答案),因此我们可以考虑和 callee 协同保存:callee 跟踪这些寄存器中的指针:
如果没有 spill,就 copy pointer map 的类型到 callee 的 map 上(caller 说是什么就是什么);
如果有 spill 这个 registers 会被存到栈上,此时就可以在 callee 的 pointer map 中找到它了;
最上层的函数没有 caller 了,如何确定 callee registers 的类型和值呢?这种情况可以 fallback 到 naive solution 上(直接推到栈上);
问题是,每个 stack frame 中都有自己的指向 heap 的 pointers,因此我们需要扫描栈上的情况。所以还需要在 pointer map 中保存 stack frame size;
边界条件:最上面的 frame 可以保存在
%rbp中;
还有一个问题,有些数据虽然是指针,但需要通过计算才能有效,这些 pointers 就是 derived pointers。例如 load a[i - 2000] 的机器含义:
xxxxxxxxxxt1 <- a – 2000t2 <- t1 + it3 <- M[t2]这时 t1 并不是有效的 object record 起点地址,只有 a 是有效的。更讨厌的是,实际情况会因为 liveness analysis 而变复杂:
xxxxxxxxxxrax <- a# a is dead hererax <- rax – 2000rcx <- rax + irdx <- M[rcx]a 生命周期结束后甚至你不能在栈、寄存器上找到它。因此我们还需要维护一个原指针和 “derived pointers” 的关系。
总结一下(左边是离线的,右边是在线的):
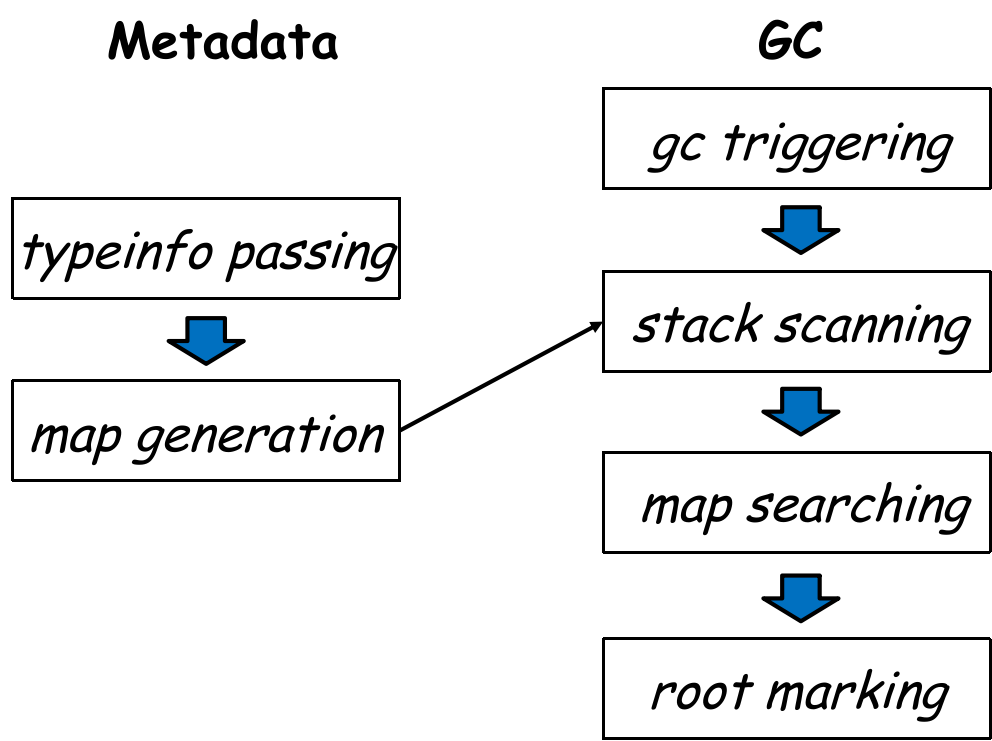
8.9 Example: Modern GC in Java
一个内存密集型设计比较成功的语言。因此 Java 的 GC 设计的比较成熟。
2010s 左右的时间,Java 使用的是 Parallel Scavenge (PS) 这种 GC 策略。
定时策略:某个 semi-space 满了后;
它其实也是一种 Generation GC 的策略(stop-copy-compact,也有 STW 存在)。不过 Parallel Scavenge 对于新代和旧代的 GC 算法是不同的。总体结构如下:
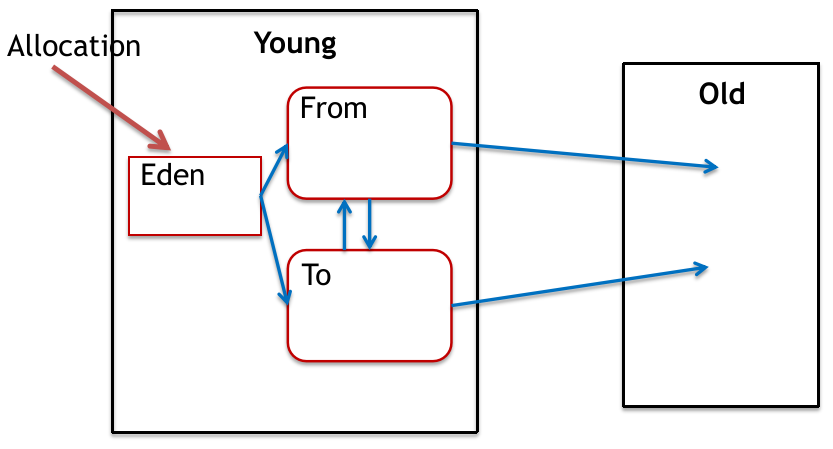
注意到,Young Generation(新代)中存在 3 个 semi space: Eden、From、To,使用 Minor GC 算法如下:
Application allocate 空间时向 Eden 区域直接插入;
Eden-space 满了后,从 root 遍历复制 reachable records 到 to-space;
当 Eden-space 再次满了/ to-space 满了后,同时从 root 遍历复制 reachable records 到 from-space;
其中在 to-space 中存活
K轮的 records,会被 promote 到 old generation(s) 中;
在一轮复制结束后,如果 from-space 快满了,则交换 to-space 和 from-space 的身份;
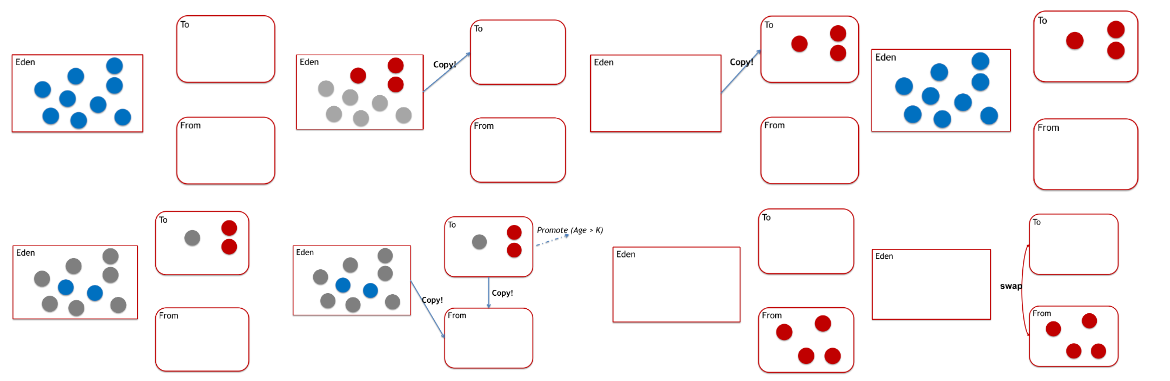
Minor GC 如何并行与 Application 执行(parallel execution)?
Reference Tracking;
Copy Race(Queue & CAS);
Work Stealing;
对于旧代(Old Generation)使用 Full/Major GC 算法:
一般要执行 Full GC,那么这时可能剩余内存已经不多了。
Marking: Mark all live objects;
Summary: Calculate new address for live objects;
先算出地址,而不是上来就 copy,方便后面的 compaction;
Compact: Move objects and update references;
需要考虑一个问题,如果 destination 也是 source 呢?

PS 这种策略也有些缺陷,例如空间是连续的(难以 split/adjust/reorganize),并且比例固定(在 VM 启动后固定):
而且 Minor GC(4 GB ~)一般在 100ms 左右,Major GC (16 GB ~)一般多于 1s。
为了改进这个问题,我们可以:
将 heap 的结构从 space 改成 regions(分块,smaller, segregated regions):
Also including young and old spaces: Adding a middleground between old and young,这被称为 Mixed GC;

Collection set: including all regions to be collected;
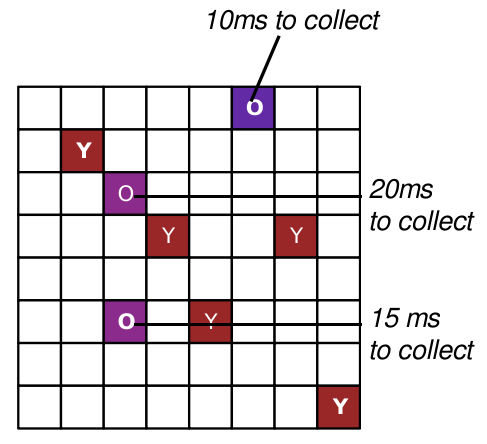
这些策略成功地提升了 Java GC 系统的灵活性和回收效率。
Chapter 9. Functional Programming Languages
什么是函数式语言?
首先,数学层面上 “函数” 指一个从元素映射到另一个元素的固定的映射关系。例如 f(x) 如果是 a,那么 f(x) 永远是 a;
这在数学上被称为 “Equational Reasoning”,或者 “幂等性”(idempotence);
在计算机语言中我们想要没有 side-effect、完全 stateless 的方法。这是函数式语言产生的一个需求原因。
另一个出发点是 “高阶函数”(higher-order functions)。人们希望将一个函数作为变量 / 参数进行传递。
目前为止,函数式语言一般可以支持:
高阶函数(返回函数的函数,即闭包);
纯函数(没有 side-effect 的函数),比高阶函数更难实现;
Lazy Evaluation(懒取值的函数),基于 pure-function;
对大多数支持函数式编程的语言,它们定义的上下文无关文法(CFG)一般如下:
xxxxxxxxxxty => ty->ty (single parameter)| (ty {, ty}) -> ty (multiple parameters)| () -> ty (no parameter)
注意到右结合的运算性质。
而且一般函数式语言的 call 方法的 CFG 和一般语言有差距:
xxxxxxxxxxexp -> exp (exp {, exp})exp -> exp ()
如果是普通语言,调用的时候只能使用 function ID 来调用,但函数式语言的调用表达式还支持对 exp 的调用(因此一般这样的语言会提供一个 Callable 的抽象,帮助语义分析等等);
9.1 Closure
9.1.1 Why?
高阶函数的很重要的特征是闭包。试想,如果我们想实现一个功能,调用一个函数获得另一个函数,例如:
xxxxxxxxxxfunction add(n: int): intfun = let function h(m: int): int = n+m in h end
var addFive: intFun := add(5)这时我们会发现在 add 返回后,add 所在栈帧就不复存在了!这个时候,如果我们想调用返回的 h(也就是 addFive),就会出问题:
因为 h 代码独立于 add 的生命周期存在,调用 addFive 时会发现 n 所在栈帧已经被销毁!
也就是我们不能用 nested function + static link 的方式处理这种调用需求。
这就是闭包需要解决的问题。
9.1.2 Implementation
一个闭包需要包含:
A pointer to the function code;
A way to access the necessary nonlocal variables (also called environment);
总之,就是代码和数据的组合;
一个语言的闭包的实现方法,还是可以用 static link 来解决,但是需要进行一些改进:我们需要把 activation records 存到堆中,而不是栈中(将 nested function 的生命周期从父函数这拆解出来);
我们在 heap 中也维护一个 frame 结构。以上面的 addFive 举例,最终的栈帧和堆的相关结构是这样的:
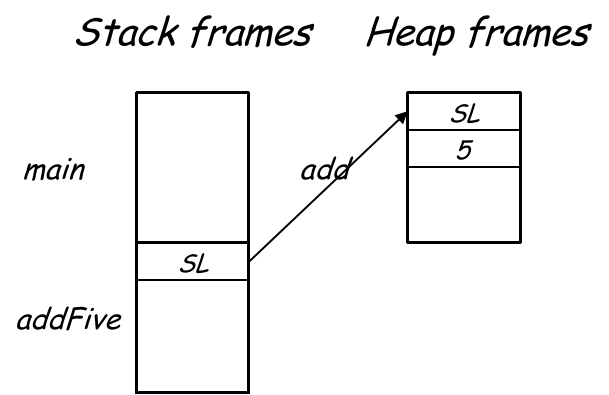
我们可以看到,这时 closure 的生命周期是取决于 function instance 的生命周期(可能是用到它的局部变量);直到这个 instance 死亡后,我们就可以从堆上释放这块空间了。
还有一个问题,为了完全脱离原来父函数的生命周期,我们还需要把中间的 escape variable 放在堆上(因为原来的策略是放在栈上,还是会随着父函数的退出而销毁)。所以索性,我们将原来所有的 escape variables 都放到栈上(包括 static link)!
然后我们在栈上保存一个 escape pointer(EP),只用来给当前栈帧的函数使用(其他栈帧的函数可以用它自己的 EP 来获得相关信息)。
也就是说 EP 是一个 non-escaping local temporary,这和之前 static link 不一样。
然后 Closure 的代码地址也作为一个 escape variable。最终,上面的 addFive 的例子中,栈帧和堆相关的实际结构如下图所示:
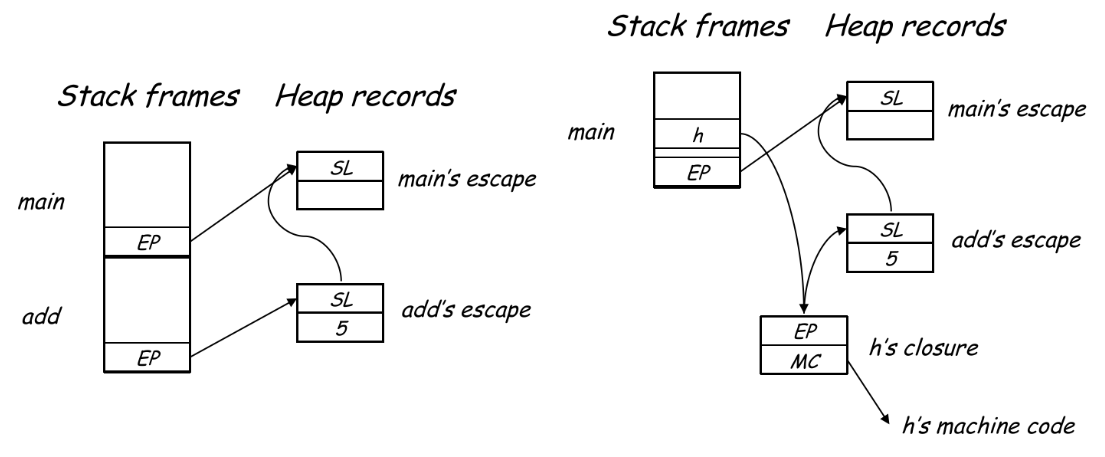
注意:以
h为例,其闭包的 record 在堆上应该是一个 function instance 就创建一个!因为我们可能创建闭包时传入不同参数,
EP的值可能不同,因此不同的 function instance 不应该指向相同的 closure record;
左边为调用 add 函数中的状态,右边为 add 返回后获得 addFive(h)后的状态。于是我们知道:
function instance 还是栈上指向 heap activation record 的;
closure 的 heap activation record 和普通的不一样。前者代码(Machine Code)和数据(指向普通 heap activation record),后者就是存放 escape variables 的空间;
static link 以及其他 escape variables 都保存在 每个函数对应的 heap activation record 中;
static link 指向对应的 heap activation record 而不是原来的栈帧的地址;
解题助记:
一切可作为变量的函数都在堆上有一个 closure record;
closure wrapper 一定有一个在堆上的 escape record;
9.2 Pure Functions & Immutable Variables
如果是一个希望没有 side effects 的函数式语言,需要任何函数都应该可以视作幂等的,原来不幂等的函数需要通过“将内部状态的描述出来”的方式来实现幂等的性质。这就是一个实现了 “纯函数” 定义的语言。
一般来说,一个语言想实现上述性质,必须禁止以下内容:
禁止在非初始化阶段赋值给变量(只能被赋值一次且必须是初始化时赋值);
不能向堆上的 records 赋值(也是初始化后不能更改);
调用 external functions 必须有可见的 effects;
例如很多常用语言中的
print()就不满足这条。因为它改变了输出流的状态,但并没有可见的 effects,因此不是纯函数;这点很严格,也是大多数实用语言不是纯函数的原因。而且这样限制会导致语言的编写并不是很方便,下面我们就能看到这个缺陷。
前面两点比较好实现,例如一个复杂的数据结构的 in-place update 可以换成 reconstruct(例如树的结构会 reconstruct,其中会共享结点),有点像 VCS 的树的构建方法。
第三点如何进行构建?答案是 continuation。它是一种描述计算机程序执行状态的抽象,类似于进程/线程的 context。这里我们可以用它来描述 I/O 相关的函数,把流的状态从函数中剥离出来,从而实现纯函数。
例如这个从 stdin 读取整型的函数,可以如此实现:

eatchar's type:string -> answer(stringConsumer);getchar's type:stringConsumer -> answer(external I/O function);getCharpasses the input character toeatChar;
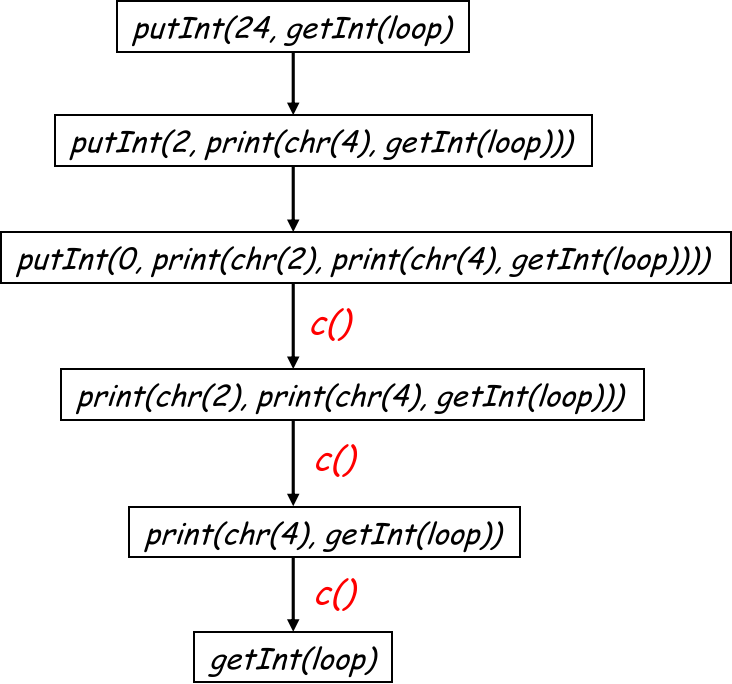
函数式的好处是方便优化,例如跨函数进行 constant propagation(变量都是 immutable 的)、inlining 都非常方便(几乎没有循环,全是递归);