Algorithm Design
Algorithm DesignChapter 0. DefinitionsChapter 1. Algorithms of Numbers1.1 数字基本算数1.1.1 加法1.1.2 乘法 & 除法1.2 模运算1.2.1 01-背包问题6.3.2 完全背包问题6.3.3 多重背包问题6.3.4 问题变种:Optimal Solution for Coins Charging6.4 最长子序列问题 II6.4.1 最长公共子序列6.4.2 最长公共子串6.4.3 Quiz: 最大连续子序列和6.5 3-Partition Problem6.6 跳石子6.7 Shortest Reliable Path (Lite) & Revisit Bellman-Ford Algorithm6.8 Revisit Shortest Paths Problem: Floyd-Warshall Algorithm6.9 Traveling Salesman Problem (TSP)6.10 Independent Sets in TreesChapter 7. Linear Programming7.1 Definitions7.3 Integer Linear Programming7.4 Dual Program7.4 Application: Shortest Path7.5 Simplex Algorithm7.5.1 算法内容7.5.2 Corner Cases7.5.3 运行时间7.6 最大流与最小割Chapter 8. NP Problems如何应对 NP 问题?梯度下降Hopfield Netural Network
Chapter 0. Definitions
介绍算法的时间复杂度(应该在数据结构中有所接触):
Big-
定义:
自反性:
常数:
乘积:
求和:
传递性:
Big-
定义:
恰好与大 O 表示法相反;
Big-
定义:
关联:很显然的,根据定义能证得:
特殊性质:
c 如果是 0,那么只有
证明:
错误证法:
Big-
定义:
Examples:
Chapter 1. Algorithms of Numbers
看两个问题:
因子分解:给定数字
素性测试:给定数字
事实上,第一个问题相当复杂,第二个问题却相当简单。
由于在
1.1 数字基本算数
1.1.1 加法
引理:任意 3 个单数位数字之和(不论进制),结果最多只有 2 个数位长。
由引理,我们讨论加法运算的时间复杂度:
假设
1.1.2 乘法 & 除法
对于乘法一般性的讨论:
假设
Al Khwarizmi 算法:
计算时, 截断除 2、 乘 2,直至 为 1,去掉 为偶数的行,将剩下行的 累加即为 的值;
使用另一种算法:
使用了 2 进制移位运算的思想,递归调用次数为
(或者说 ,这里以数位 来衡量)次(将 折半的次数),每次递归中:一次右移、一次奇偶测试、一次左移、可能的一次加法,因此时间复杂度 ;
考虑除法?
1.2 模运算
本节需要线性代数、抽象代数相关知识。
几种理解方式:
能被 整除;
除以 会余下 ,或者说, 模 等于 ;
和 模 同余(一个等价类);
我们讨论一个 mod N 的系统,按照 mod N 运算能将整数集划分为 N 个等价类(数学上可以证明:自反性、对称性、传递性),于是在讨论 mod N 的代数系统中,我们总是选取
对于定义在集合
封闭性,即
结合律,即对于
单位元存在性:
逆元存在性:
这个代数系统就被称为 “群”(Group)。
特别地,当
最小非负完全剩余系(Minimal Non-negative Complete Residue System),记作
我们接下来定义在这个系统
我们先在整数集上观察模运算的性质:
替换准则(可以看成等式的性质):
替换准则理解为,两个数相加、相乘,其最终的余数也相加、相乘;
结合律:
交换律:
分配律:
结合、交换、分配律理解为,加法结合、乘法交换、分配不会影响同余性(仍然位于一个等价类,属于一种等价变换);
上面的性质说明:在一系列基本算数运算过程中,模运算可以在任意阶段进行:
也就是说在整数集上:
不讨论除法,而是讨论乘法逆元!
于是我们定义在
其中注意乘法逆运算的定义:
含义就是,如果在
注:
上的等式一般写在 mod N 标记的左边,并且用等价符号表示。也就是说,在一般整数域上 可以写成 ;
1.2.1
整个计算过程包括:一次加法、一次可能的减法,因此时间复杂度
模的除法会涉及 0 的情况,比较复杂,后面推导;
1.2.2
也就是说,
这是指数时间复杂度的算法,不能这么解决问题。
我们想到可以每次计算之后不止乘一次,而是平方一次,这样能大大加快计算速度:
这样可以列出公式:
1.2.3 Euclid's Greatest Common Divisor
定义
特别地,
;
Euclid 发现,对于正整数
两个正整数的最大公因数,为其中一个较大的数模另一个数的余数,与另一个数的最大公因数。
要证明上式,只需说明
证明等式,将其分解为两个不等式:
一切能整除
同理,一切能整除
如何估计这个算法的时间复杂度?
引理:
证明引理分
和 两种情况:
时,显然有 ;
时,则显然有 ;
所以可以知道,
综上,GCD 算法时间复杂度
1.2.4 Euclid GCD 算法的延伸
我们知道如何求两个正整数的最大公因数。考虑新的问题:如何验证两个正整数
仅验证整除性肯定是不够的,所以我们再引入一个引理:
如果
证明引理,将等式拆成不等式:
显然由公因数的条件得:
; 另一方面,由于
为 的公因数,又由于 ,因此 一定能整除 ,即 为 的因数,故 ; 得证;
现在讨论 “扩展 Euclid 算法”:
xfunction extended_Euclid(int a, int b)// Input: a >= b >= 0// Output: Integer x, y, d, such that: d = gcd(a, b) and ax + by = d
if b == 0: return (1, 0, a)(xp, yp, d) = extended_Euclid(b, a mod b)// 多了一步迭代计算 x 和 yreturn (yp, xp - [a/b] * yp, d)再引入一个引理:
对任意正整数
证明上面的引理,观察到这是个递归算法,因此可以考虑从递归终止条件归纳证明。
借助
的信息,使用归纳法证明:
(奠基)当
时,显然(?) (假设)假设当
时( ),算法是正确的; (归纳推理)则注意到
,因此可知调用返回的 中 是正确的; 记
,则 ; 这说明
其中 ;
人手工应该如何计算 “扩展 Euclid 算法” 的答案呢?
为了找到
用 Euclid 计算出
先用
最终会得到
值得注意的是,扩展 Euclid 算法涉及数论中的重要定理:
裴蜀定理:设
为正整数,则关于 的方程 有整数解当且仅当是 的倍数。
此外,扩展 Euclid 算法可以应用于:
计算不定方程
判别
计算
……
注,由裴蜀定理可以证明以下结论:
方程
的特解 可以由扩展 Euclid 得到(或者瞪眼法),通解可以写成:
有了这个方法,我们可以讨论
1.2.5
回顾在 1.2 开头对于
理解为,在整数域上,对于一个整数
,可能存在另一个数 ,使得 被 除后余 1; 或者说,在
系统中,两个元素的乘法结果为 1;
引出可以被数学证明的定理:
对于任意的
证明:如果
关于不可能大于 1 的证明,使用反证法易得。
如果
总结:
基本加法:
基本乘法:
基本除法:
总结两个定理:
Euclid + 扩展 Euclid:两个整数的最大公因数,以及一个构成式
1.3 素性测试
1.3.1 Definitions
引入 费马小定理:
证明:
取
为模 的所有非零整数的集合,即 , 可以证明,有序集
和 形成一个简单排列变换。 也就是说,
和 一定不相同,并且不重复、都位于 内; 因此可以将两边的等式相乘:
; 再由
为素数可知 和 互素,因此消去 得:
;
我们用费马小定理就能判断素数了吗?可惜不行,因为这不是充分必要条件。
事实上存在一些数
也就是说,对所有与
如果
与 不互素,则 ,肯定无法通过费马测试。因此这里只需要看与 互素的 ;
因此,在不考虑 Carmichael 合数的情况下,所有其他合数
对与
证明:
假设某个
使得 ,那么对于任意通过了费马测试的 ( )都有 无法通过费马测试:
; 并且:对所有给定的
,当 不同时, 对应的 总不会相同(证明同费马定理,如果 , ,则可知 ,其中 ,与 的假设矛盾)。 所以存在
一一映射(能通过 -> 不能通过),又多出来一个 不能通过,因此:非 Carmichael 合数 一定有至少一半无法通过费马测试的 ;
所以:
我们只要重复 100 次,整个算法对于所有的
补充:Monte-Carlo Algorithms & Las Vegas Algorithms
Monte-Carlo Algorithms:时间复杂度确定,但算法正确性是个概率(例如这里的 prime test);
Las Vegas Algorithms:时间复杂度不确定,但算法正确性确定(例如 quicksort);
1.3.2 随机生成素数
引入 Lagrange 素数定理:
令
这说明:
素数有无限多个,只不过越大越稀疏而已;
随机的
位数字 (回忆 ),是素数的概率为 ;
我们根据上面的理论依据设计一个生成
随机生成一个
对
由于对于随机整数
1.4 密码学
基本设定(roles):Alice & Bob 传递信息,不希望 Eve(偷听者,仅尝试在不被发现的情况下获取 Alice 和 Bob 交换的信息)和 Ida(中间人,它可以打破通信的规则,例如伪造身份等等,也可以做 Eve 的窃听行为)知道消息;
如果 Alice 直接向 Bob 发送原封不动的消息(称为 “明文”),那么 Eve 可以直接监听到、Ida 还可以直接进行内容篡改。
1.4.1 对称加密
所以可以采用一种简单的做法来尝试防止 Eve 和 Ida 的行为:
Alice 和 Bob 约定一个函数
其中这对函数有一些硬性要求:
在发送消息
形象理解就是一把暴露在外的锁(
Sidebar:按位异或 与 AES 算法
按位异或(bitwise exclusive-or)就是一种选择。
;
; 因为它满足一些优秀性质:
是一个双射函数,其逆函数就是自身;
能保证
和 的关系不大。只要密钥 是随机的,那么 的每个二进制位有 50% 概率不变,有 50% 概率相反; 硬件计算很快,性能好;
但这个函数的
参数不能重复使用相同的随机数。为什么?因为重复的 会让窃听者获取和明文相关的消息:窃听者第一次拿到 ,第二次拿到 ,那么就知道 ;这个 就会间接地泄漏信息。 假设通信传递的是某个重要选举的票选信息,而每一位代表一个票选意见(比如是 1 就选 A,是 0 就选 B)。那么
中的 0 越多,说明选举群众的共识度越高,有更多的人选择类似。 为了解决这个问题,人们基于按位异或设计了一种更强的对称加密算法:AES(Advance Encryption Standard),它的好处是:
虽然算法公开,但可以重复使用密钥;
计算效率合适;
目前没有比 brute-force 更好的办法来破解(但也没有证明绝对不可破解);
这种方式被称为 “对称加密”(Symmetric Cryptography),即加密、解密用的密钥相同。
而
对称加密特点:
计算量小,吞吐量大,传输大量数据不会因为加解密成为性能瓶颈;
在不知道密钥信息的前提下,窃听者、中间人无法破坏通信的安全性;
但对称加密也有问题:在 Alice 和 Bob 第一次交流的时候,肯定需要约定一个密钥
也就是说,对称加密使用的密钥目前还没有办法保证不被网络上不可信任的设备截获。
因此需要更强大的措施来防止窃听者、中间人获取密钥。
1.4.2 非对称加密
假设我们通过某种方法获得了一个神奇的算法:
Alice 使用
也就是说,加密用的
相当于一把双钥匙锁:只能用

在通信前,Alice 先用某种方法生成一对
对,就这一个更改就让 Eve 没办法了:
因为虽然
这个公开的
而私钥加密、公钥解密的过程被称为 签名(signing);
Sidebar: RSA 算法
那么上面的 “神奇算法” 是如何实现的呢?数学家想出一个方法:
任取两个相当大的素数
,计算 ; 找到一个和
互素的数 ,则 是 上的双射,作为我们的加密函数; 解密相当简单:找到
关于 的乘法逆元,记为 ,则对 上的任一元素 ,都有: ; 证明:由于第 3 条蕴含第 2 条,所以下面仅证明第 2 条:
注意到
可以进行因式分解: ; 再由费马小定理:
( 是素数),因此对于素数 , ;即: ,或者说 得证; 也就是说,
是公钥, 是私钥, 是加/解密函数。 由我们前面讨论的知识,随机生成两个素数时间复杂度
,加密 / 解密是 指数 ; 这个算法安全的前提是,没有人能快速地从
获得 (即:素因数分解是难问题);
但是非对称加密也有缺陷:无论是生成公私钥,还是加密数据,计算都相当复杂、性能不佳,不适合用来传递大规模数据。
于是,一般可以采用这种措施:非对称加密 先用来传递对称加密的密钥,然后之后的通讯就使用对称加密来通信。这样既利用了对称加密的特性(计算量小、不知道密钥的情况下基本没法破解),又利用了非对称加密的强大安全性。
1.4.3 证书
现在 Eve(窃听者)彻底没法窃听到任何有效数据了,但是 Ida 还有办法。
Ida 可以拦截 Alice 和 Bob 间的所有流量,然后在 Alice 向 Bob 第一次发送密钥时:
截获 Alice 的公钥,自己再重新生成一份新的公私钥;
用 Alice 公钥解密、用自己的私钥加密,最后把自己的公钥交给 Bob;
Bob 以为这是 Alice 的公钥,解密也能成功,殊不知用的是 Ida 的公钥;
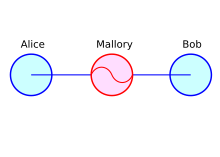
这下,Alice 和 Bob 在不知情的情况下,把消息全都发给了 Ida,Ida 既掌握解密的公钥、所有消息,还能不被 Alice 和 Bob 发现。
Ida 在这里被称为 “中间人”,而这种行为被称为 “中间人攻击”(Middle-in-the-man Attack,MITM);
这样是不行的。不过往好处想,还是之前的说法,只要我们保证第一次交换对称加密密钥的过程是安全的不就行了?这里的问题在于 Ida 可能会篡改公钥;
那么有什么办法是在暴露公钥的情况下,还能防止公钥被篡改的?
这理论上肯定没法只由 Bob 和 Alice 解决,还需要外界的帮助。于是人们引入了 “第三方公证” 的机制:
人们需要设立一个第三方机构,确保它不会与中间人勾结。第三方机构本身事先生成一对公私钥,然后:
Alice 在将用自己的私钥加密的 “对称加密密钥” 传给 Bob 前,先传给第三方机构,让第三方机构用它自己的密钥再加密一次;
Alice 将第三方加密后的密钥传给 Bob,Bob 使用第三方公开的公钥解密,再用 Alice 的公钥再解一次密,就能安全拿到接下来要进行对称加密的密钥了;
由于 Ida 无法伪造第三方机构,因此最外层的密钥没法突破,因此也没法得到里面的数据进行中间人攻击了。
这里,第三方机构(证书签发机构)提供的公钥被称为 “证书”(Certificate)。Alice 使用第三方公钥加密、Bob 将加密信息给第三方解密的过程,就称为 “证书签名”;
目前,这套机制能够完全防御 Eve(窃听者)、Ida(中间人 / 攻击者)对信息的窃听和篡改。当然,证书 + 非对称加密 + 对称加密的整套机制被应用在了 SSL/TLS 当中,为 HTTPS、SSH 等协议重要通信场合提供全面的保护。
Chapter 2. 分治算法
2.1 更快的乘法
引理:对任意正整数
,总存在一个 使得: ,其中 是 2 的非负次幂;
高斯发现,一个复数乘法:
也就是说乘法次数从 4 次变为 3 次;这对于单次计算来说没什么(常数优化),但在递归的用法时会获得极大地提升:
我们把将两个数
那有人会说,这不还是这么算吗:
不过你再考虑一下之前高斯提出的优化呢?计算
这样递归时间复杂度就变为:
注意,
和 的位数可能达到 位,但是在推导中无关紧要,所以写成 ;
想象成一棵三叉树(因为 3 次乘法),每层中结点的
在第
注:指数换底
;
所以 时间复杂度为
事实上还能做得更好(快速傅里叶变换),以后介绍。
2.2 更一般的分治递推分析
在解决
为分支因子, 为规模缩放因子;
因此这样一般的问题的时间复杂度计算法为
推导过程可以直接假设
为 的幂,因为无论 的某个整数幂与 相差再大,总不会超过 (也就是 ), 因此我们可以直接忽略
造成的舍入影响。 证明:
树高
,第 层每个子问题规模 ,第 层共 个子问题,第 层总体规模 ; 问题总体规模:
; 注意到
和 1 的大小需要分类讨论后才能代入等比级数求和:
若
,即 ,此时 ; 若
,即 ,此时 ; 若
,即 ,此时 ; 记忆方法:
和 谁大以谁为幂;一样大则 和 都有;
2.3 应用:比较排序的时间下界
我们首先讨论归并排序。
算法描述:对于长度为 merge(),返回 merge 的结果;
显然这里
merge 两个有序数组的方法是,用两个指针放在数组第一元素位置并比较数,较小(如果从小到大排)的先放到最终数组中,并将指针后移;直至一方的指针遍历结束,另一方直接将剩余部分复制到结果数组中,我们认为复杂度
这里看到
在上升到更一般的层面:所有的基于比较的排序都可以看成是一棵比较树,这一定是一棵二叉树,因为一次只能比两个数(以一个 3 个数间最少次数比较的排序为例):
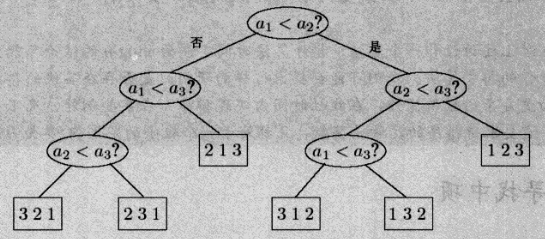
所以,这一定是一棵有
以相同结点数量下最矮的二叉树——满二叉树为例(事实上达不到),树高
证明
使用斯特林公式证明:
2.4 应用:中位数算法再讨论
我们讨论过 Top-K Problem:理论最小时间复杂度
一开始是小顶堆出队:
本章我们讨论分治策略。说到分治策略解决 Top-K Problem,就不得不提快选算法。
随机 pivot 的快选算法:
我们再来详细分析它的时间复杂度。
假设我们认为,如果选到 25% ~ 75% 分位的数是好的选择。因此随机选 pivot “是好的” 的概率为 50%;
另外,概率学认为平均 2 次随机选择会选到 “好的” pivot。证明:
设 “选到好的 pivot” 作出选择次数的期望是
所以在选择好的 pivot 的情况下,我们每两次最少能排除掉
根据 master theorem:其中
2.5 应用:矩阵乘法
20 世纪,有人发现 2 x 2 的矩阵乘法计算只需要 7 次乘法(原来需要 8 次)。
这看起来没什么,不就是常数时间的优化吗?你错了!因为矩阵乘法可以分块,这意味着对于
由
2.6 应用:计数逆序
考虑一个问题:
对 n 首歌排序,两种排序方法的相近程度可以使用某个 metric 来描述。这个 metric 被称为 “计数逆序”;
定义计数逆序:以任一个排序方法为基准,另一个排序方法中,所有元素间出现逆序的次数称为 “计数逆序”;
为了方便讨论,我们以一个顺序序列作为基准(例如 1~N),给定一个输入序列,问题转换为判断这个输入序列和基准序列间的计数逆序。
普通思路是直接先排序再计数,时间复杂度
(要知道所有元素的逆序次数),但是多做了很多事,必然可以优化。
现在发现,计数逆序的求解也可以通过分治法完成。考虑分治法如何 combine two subproblems:
对两个子问题序列
如果
因此考虑如果
但子问题合并的时间复杂度是
能不能更简单?可以。我们可以在
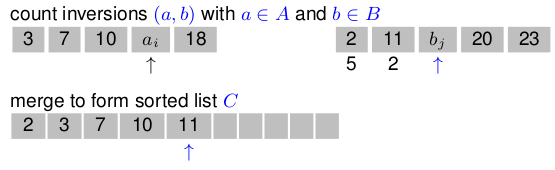
假设过程采用从小到大排序。让
对另一个序列
如果
如果
重复上一步,直至有一方遍历结束。如果基准序列
由于这是从头到尾读一遍而已,和 merge sort 的情形一致,因此新的合并复杂度
所以,问题整体可以用分治的排序来顺便计算,时间复杂度
这种算法的名称就称为 sort-and-count algorithm;
Chapter 3. The Algorithms using Fast Fourier Transform
3.1 Revisit Complex Number
复数的基本运算
直角坐标下,
在极坐标表示下,
复数相反:
乘法法则:
如果
复数等式
于是解可以表示为:
感性地想象:由于
因此反过来
所以很显然,
由于复向量本身就可以用复数一一对应,因此我们可以把
注意到比较有意思的现象:当
共轭复数:
3.2 Begin with The Production of Polynomials
考虑一个问题,现在我们希望计算两个两个同次多项式之积:
答案会是这种形式:
假设乘积和加法数字不大(和前一章讨论以数位为
能否简化这个时间复杂度?
再注意到数学上的事实:
相关系数表示法:
值表示法:
而
所以我们想,更简单的算法应该是这样的:
(选取 & 计算)分别为
(相乘)利用选取的点,计算在
(插值)将这些
现在我们不清楚插值的时间复杂度能到多少,先放在一边,不过我们可以使用特殊的方法来优化第一步
为了加快从系数表示法到值表示法的计算速度,我们可以选取一些特殊的点:正负点对(
偶数次幂相同(省去计算);
奇数次项相反(取反);
这么优化是常数时间的,还远远不够。
我们还要借鉴分治法的思想,我们发现:
其中
包括了 偶数系数的多项式、 是奇数项的系数的多项式,二者的次数不超过 ;
也就是说,通过把奇数次项提出一个
现在给定正负点对
这样
假设我们能一直这么递归下去,那么:
讨论
由 master theorem 可知
可惜的是,我们并没有办法一直这样持续下去,因为在实数范围内
这个时候就需要用到复数了:
我们取的
无论如何,现在我们只需要输入一个满足上面条件的
而在
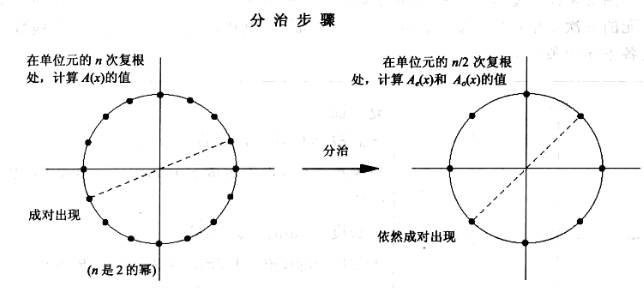
现在我们描述这个 FFT 算法:
xxxxxxxxxxFFT(A, w)input: coefficient reprentation of a polynomial A(x) of degree ≤ n − 1, where n is a power of 2; ω, an n-th root of unityoutput: value representation of A
if w == 1 then return A(1); // w = 1 说明当前 A 的次数最大为 1express A(x) in the form Ae(x^2)+xAo(x^2) // 其中 Ae、Ao 都用向量表示// 递归计数 Ae(xi^2) 在 1, w^2, w^4, ... 共当前一半数量的点处的取值,// 其中在 1, w^2, w^4, ... 中相反数成对存在call FFT(Ae, w^2) to evaluate Ae at even power of w;// 同理,递归 Ao(xi^2)call FFT(Ao, w^2) to evaluate Ao at even power of w;
// 真正计算 1, w, w^2, w^3, ..., w^{n-1} 的点,其中 n 为满足 e^{2pi*i/n}=1for j = 0: n - 1 do // 这里注意 1, w, w^2, ... 这些点也是正负配对的, // 因此实际操作可以同两边开始,一对一对地计算以减小计算量。 compute A(w^j) = Ae(w^{2j}) + w^j * Ao(w^{2j})endreturn (A(w^0), A(w^1), ..., A(w^{n-1}));注意到,在某层递归中,计算
和计算:
可以成对处理。
在递归下去的
这样,第一步的 “选取计算” 环节已经被我们成功降到了
我们注意到,如果得到了结果多项式的值表示,要反过来求系数,就是在解这个线性方程组:
注意到中间的矩阵是范特蒙德矩阵,记为
为什么我们能大胆求逆?因为一般矩阵高斯消元是
为什么这么说?回想我们之前代入的
这个矩阵中
“对称”性:
正交性:
归一性:
因为
而这个矩阵正是快速傅里叶变换,在变换向量
这样,由
和前面的 evaluation 的计算方法不是几乎一致吗!前面给
在代入前面的算法之后在除以
Chapter 4. Graph
4.1 Revisit: DFS in Graph
首先定义一些本章会用到的方法:
xxxxxxxxxxprocedure EXPLORE(G, v)input : G = (V, E) is a graph; v ∈ Voutput: visited(u) to true for all nodes u reachable from v
visited(v) = true;PREVISIT(v); // 定义一个在 visit 前的活动for each edge (v, u) ∈ E do if not visited(u) then EXPLORE(G, u);endPOSTVISIT(v); // 定义一个在 visit 后的活动xxxxxxxxxxprocedure DFS(G)for all v ∈ V do visited(v) = false;endfor all v ∈ V do if not visited(v) then Explore(G, v);end
4.2 无向图的连通分量
多次 DFS 计算连通支数:通过在
PREVISIT(v)中定义ccnum[v] = current_cc,然后current_cc在每次 DFS 后自增;最终可以得到总连通支数、各个顶点所属连通支情况;
定义结点的 “生命周期”(从 pre visit - post visit),用
pre[], post[]表示,可以定义:xxxxxxxxxxprocedure PREVISIT(v)pre[v] = clock;clock++;xxxxxxxxxxprocedure POSTVISIT(v)post[v] = clock;clock++;则有引理:
对图中任意两结点
[pre(u),post(u)]和[pre(v), post(v)]要么是彼此分离的(disjoint),要么是一个完全包含另一个的;这似乎不难发现
证明:
反证。假设生命周期存在 overlap,即
pre(u) < pre(v) < post(u) < post(v),则由pre(u) < pre(v) < post(u)可知,结点post(v) < post(u),这与post(u) < post(v)矛盾,因此原命题得证;
注意,每次 DFS 后 pre 和 post number 不会重置,各个顶点的 pre/post number 只会增大;
4.3 有向图的连通分量
我们已经了解,对有向图 DFS 会生成深度优先森林(DFS Forest)。
于是在有向图、DFS Forest 的定义的基础上,引入新的定义(定义有向图
Tree Edge(树边):一条原来在有向图
Forward Edge(前向边):一条原来在有向图
不是树边,而是指向间接后继结点;
Back Edge(回边):一条原来在有向图
不是树边,而是指向祖先结点;
Cross Edge(交叉边):一条原来在有向图
不是树边,指向 siblings 一族结点(既不是祖先结点,也不是子孙结点);
我们将结点生命周期考虑进来,针对一条有向边
树边、前向边总是满足:
回边总是满足:
交叉边总是满足:
能否证明有向图
由上一节的证明可知,如果要有其他类别,则一定是
假设生命周期表示为
4.4 有向无环图(DAG)
给出引理:
一个有向图
证明:
充分性:若
必要性:反证。假设
因此我们知道,在 DAG 中不存在 back edge。而只有回边 post(v) < post(u),并引出另一条引理:
在 DAG 中,每一条边总是指向 post number 减小的方向。
至此我们发现:一个有向图:无自环、可线性化、无回边实际上相互等价(是同一件事);
进而:DAG 中,post number 最小的点一定是汇点(出度为 0),post number 最大的点一定是源点(入度为 0);
由于正整数集上的可比性,DAG 上所有结点中必定有 post number 最大的,也必定有最小的,即证明了另一条引理:
每个 DAG 中,至少有一个源点和一个汇点;
因此,我们找到一种线性化 DAG 的方案:找到源点(post number 最大点)删除并输出,重复这个过程直至图为空;
4.5 Revisit: 有向图强连通分量
我们已经知道:
两结点间存在一条从
两结点间仅存在一条从
两结点间 不考虑所有道路的方向(称为“有向图的底图”),若这两个结点连通,则称
而且:
有向图 G 中任意两结点间都是强连通的,则 G 为强连通图;
G 的强连通子图 H 不是 G 的任何其他强连通子图的真子图,称 H 为 G 的一个极大的强连通子图,也称强连通分量;
另外,我们在有向图中讨论 “连通”,一般都指 “强连通”,除非额外说明。
现在,我们将一个有向图按强连通分量划分为若干个不相交集,如果:
将强连通分量顶点和内部边组成的集合看作一个超结点;
若划分时两个超结点内部结点间可达,则两个超结点连有同向有向边;
则一定会得到一个 DAG,我们称这种形成的 DAG 为 embedding graph(嵌图);
这就是引理:任意一个有向图的 embedding graph 一定是 DAG;
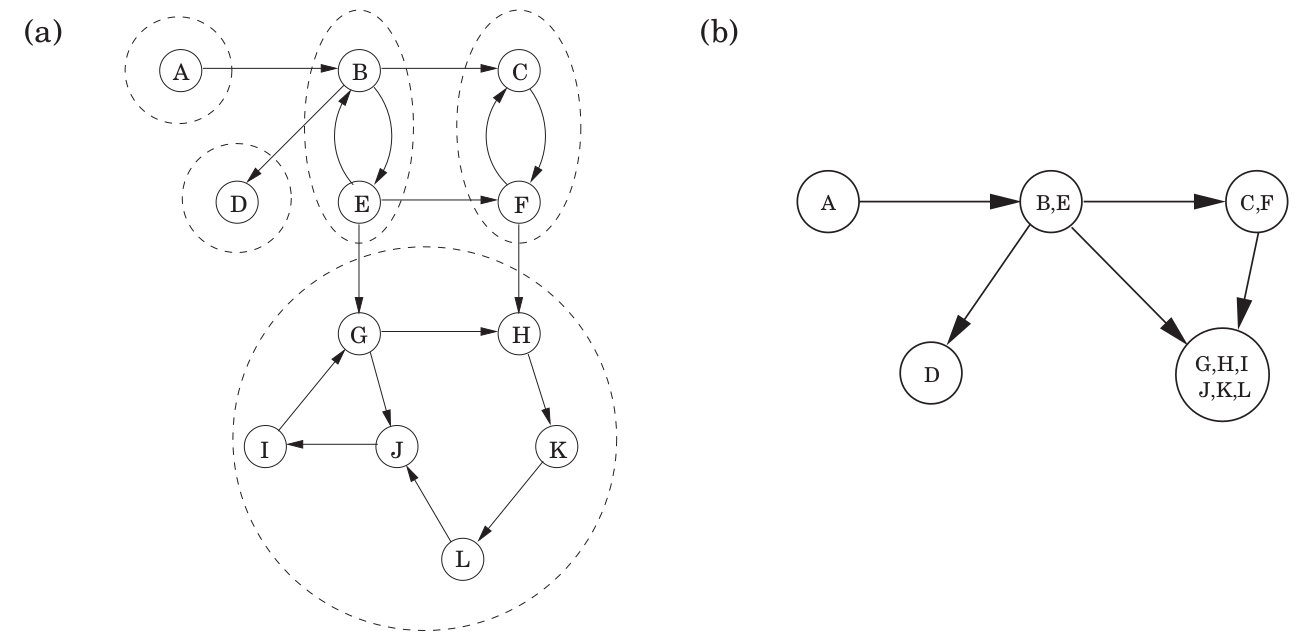
引入定义:源/汇点强连通分量:一个有向图中,它的 embedding graph 中源/汇点对应的强连通分量;
现在考虑如何找出任意一个有向图的强连通分量。
现在已知已经存在了有效的求解强连通分量的算法,线性时间复杂度,它主要基于一些性质:
DFS 的 explore 子过程如果从结点
这个性质告诉我们:如果在一个汇点强连通分量的任一顶点调用 explore 子过程,则恰好能获得这个强连通分量;
为什么必须是汇点?不然这个超结点出度不为 0,调用 explore 会出这个超结点,或者说可达结点在这个超结点之外也有;
问题是:
如何确定一个有向图的汇点强连通分量中的一个顶点?
通过这个性质获得了汇点强连通分量后,下一步应该怎么办?
针对第一个问题,我们率先给出了下面的性质:
在 DFS 中 post number 最大的点一定位于其中一个源点强连通分量内;
注意,post number 最小的点不一定在汇点强连通分量内,因为原图不是 DAG。这个 “post number 最大的点一定位于源点强连通分量” 的规律是比较特殊的。
由于证明它需要另外一个性质,因此先介绍:
若
现在先证明这条性质:
设顶点
如果 DFS 遍历从
如果 DFS 遍历从
综上,这条性质得证;
再证明上一条性质:
由第三条性质可知,一个有向图的 embedding graph 中的任意一条有向边
有了 2、3 两个性质,我们能解决:“如何确定一个有向图的汇点强连通分量中的一个顶点” 的问题。
我们找到一个有向图
证明:
这样,我们借助第 2 条性质,在
接下来我们如何做来继续找图
在
从
PREVISIT中设置ccnum[])找到汇点连通分量中的所有顶点,在一轮 DFS 结束后,找到剩余结点中 post number 最大的
这个算法的时间复杂度是线性时间的,但是在很大的图中,这也是不可行的,因此目前有学者已经提出了
考虑习题:
Give an efficient algorithm which takes as input a directed graph
, and determines whether or not there is a vertex from which all other vertices are reachable.
如果这个点存在,那么它一定在源点强连通部件中(反证法);
找到任意一个源点强连通部件,做一次 DFS,如果没有遍历完所有顶点,则不存在;反之存在,并且这个强连通部件中的所有点都符合题意。
4.6 BFS in Graph
我们知道 DFS 可以找到图两点间的连通性,但是对于两个点间的最短距离却不清楚。我们可以利用广度优先搜索(BFS)来确定两点间的距离)。
我们本章认为 BFS 是先入队、更新距离,之后再出队。
并且和 DFS 不同,我们只关心同一个强连通分量中的距离情况。
有个 lemma。BFS 过程中,对每个
所有与
其他顶点的距离都还未被设置(
队列中只含有与
可以证明:当前队列中的所有结点总小于下入队一元素的距离;
这个 lemma 形象地说明 BFS 是“按层输出”的。
4.7 正权图中两点间的单源最短路径
我们知道 BFS 只能知道等边权情况下的两点距离。如果我们需要将边长(边权)考虑进去,则就没法适用。
一个改进方法是,按边权数量大小增加该边上的结点(对
但这种方法的时间复杂度
再改进一些,就是 Uniform Cost Search;算法的思路是:
使用优先级队列保存结点队列(准备访问的结点),先入队起点;
总是从优先级队列中取出准备访问的结点中 cost 最小的结点,更新最短距离情况;
如果存在最短距且更小,则什么也不做,继续出队;
反之,更新这个结点的最短距,并且更新
pre[](总是指向当前结点最短距的前一个结点,通过这个就能在最后避免回溯地获得任意结点最短路径);如果没访问过这个结点,则将结点入队(Tree Search 不做这步);
最终队列为空停止;
Dijkstra Algorithm 就是在这个算法的基础上,先将所有结点构建优先级队列(比逐个插入更快),然后通过手动出队、手动减小更新后的元素优先级、通知优先级队列调整被减小键值的元素(就是 decreaseKey),达成上面的目标。
所有结点初始化距离为
在队列不空时循环出队:
出队
pre[](如果需要);
注意
上面的 pre[] 用到了两个性质:
子路径最短性:如果
子路径距离可加性:
注意到我们可以用相似的思路,让我们把所有顶点都先放到优先级队列中(减小出入队的开销),然后遍历点是动态地更新点的最短距(也就是改变优先级队列中某元素的优先级),当我们确定下某个点的优先级后,直接将它出队,这就是 Dijkstra Algorithm;
现在我们关心这个 “优先级队列” 的实现,以及它对于各种操作的复杂度。
众所周知,优先级队列通常使用堆来实现。我们比较常用的数据结构在 Dijkstra 算法中的使用的操作的耗时情况:
| Type \ Aspect | delete min | insert/decreaseKey | |V|×deletemin+(|V|+|E|)×insert |
|---|---|---|---|
| Array | |||
| Binary Heap | |||
| d-ary Heap | |||
| Fibonacci Heap |
因此有这几个事实:
当图的边稀疏时(
当图的边相当稠密时(
4.8 含负权无负环图中两点间的单源最短路径
如果一个图中存在负值的边权,那么为什么 Dijkstra Algorithm 不再适用了?
我们回顾 pre 用到的两个性质,子路径最短性、子路径距离可加性 都没有违反!
那究竟是哪里出问题了?实际上是这个假设:从起点
也就是 Dijkstra Algorithm 总是从当前最近到远的方法依次更新最短距,但是如果远处有个负值会降低路径总长度,那么需要重新更新这条路上所有已经确定最短路径的顶点。
更严谨地说,我们应该从如何证明 Dijkstra Algorithm 的角度下手,看看究竟哪个证明步骤不再成立。
原先我们使用归纳假设证明 Dijkstra Algorithm:
作出假设。在每次更新一个结点
的所有相邻结点位置后(每一轮 while 循环后),有下列条件成立: 条件 1. 存在一个值
,使得从 到全部已出队结点集 中的所有顶点的距离都小于等于 ,同时 到 外所有顶点的距离都大于等于 ; 条件 2. 对每个已遍历的顶点
,从 到 的最短路径上的所有点都在 中;
奠基。
时(起点),上述假设显然成立; 归纳推理。下一轮更新时,将出队
( 加入 )并更新 的所有相邻结点 。接下来需要: 证明条件 1 仍然成立:由于
和 中的最短距离一定是正值,因此 满足条件 1; 证明条件 2 仍然成立:我们设从
到 最短路径上的上一个顶点 ,由子路径最短性(显然成立,否则可以找到更短的,没有借助边是正值的条件)可知,这条路径上的 到 的子路径一定是 到 的最短路径。由上一轮假设的条件 2,从 到 路径上的所有点都在 中。 由于
刚入队,即 ,因此边 上的两个顶点都在 上,所以 到 最短路上所有点也在 上。条件 2 仍然成立。 综上,我们证明了在 Dijkstra Algorithm 的每轮 while 循环上,都有条件 1、条件 2 成立。
现在如果我们要知道
到 (目标结点)的最短路,那么我们一定可以通过 Dijkstra Algorithm 逐步找到最短路上的各个顶点,最终达到 ;这就是 Dijkstra Algorithm 的正确性。 我们发现,如果边不再是正数,那么归纳假设中就没法证明条件 1 了!
也就是说,可能存在一个在未出队(
以外)的结点 ,其值也小于 ,这就说明我们没法保证最短路 中 一定比 离 更近(也就是 会普遍比其他结点“更难”出队、更后面出队),又由于 Dijkstra Algorithm 没法更新已经出队的结点的最短距,因此没法找到这条最短路径!
sidebar:那么能不能同时加上负值的绝对值最大值来转换成非负权的问题?不行。因为最短路中每条边被使用的次数不一样,因此这样转换没法等价为原问题。
所以本质上,Dijkstra Algorithm 无法求单源含负权图的最短路,就是因为没法更新出队后的结点最短距,因为它认为先出队的结点一定能更近地到达目标结点!
所以 “乱拳打死老师傅”,我们只要更新最短距的次数足够多、足够充分(没有 side effect 的话),那一定能知道真正的最短路。事实上也确实是这样,这就是 Bellman-Ford 算法:
xxxxxxxxxxprocedure BellmanFord(G, l, s):(V, E) = Gfor all u in V: dist(u) = infinity prev(u) = nil
// start pointdist(s) = 0repeat |V| - 1 times: for all e in E: update(e)
procedure update((u, v) in E):dist(v) = min{dist(v), dist(u)+l(u,v)}这个 for all e in E 的遍历是有说法的,这不仅仅是 Dijkstra Algorithm 的一次 while 循环(确定已知顶点的相邻顶点的最短距),而是:
从顶点角度看:没有出队地确定 “所有已确认过最短距的顶点 + 未确认的相邻顶点” 的最短距;
从边的角度看:只要边有一个顶点的最短距不是无穷,就更新这条边两端顶点的最短距;
于是重复
补充:负环问题 & 最简最短路
显然,如果一个图含有负环,那么就别想求最短路了,因为最短距是负无穷。
但是如果我要求的是最简道路(不含重边和环的道路)中的最短路呢?那又可以求了!
4.9 含负权的 DAGs 中两点间的单源最短路径
如果是 DAG,那么借助这个好的性质,单源最短路径的算法甚至可以优化到线性时间。
我们知道 DAG 可以线性化,那么很显然,按照线性序的顺序访问各个顶点,直接按照沿途的边来更新结点最短距,那一定可以获得各个结点最终的最短距。
算法很简单,就是先做一次拓扑排序,标记顺序后,沿顺序遍历点,更新点的所有相邻结点的目前最短距(不继续展开,而是跟从外层循环给定的顺序),时间是线性的。
如果要求 DAGs 最长路,那么把所有边权全部转为相反数,使用求 DAGs 最短路的方法即可。
考虑问题:
有向正权图中最简最长路径?
NP Hard 问题。
有向正权图的最短环?
对每个点使用一次 Dijkstra Algorithm,找到它与其他顶点的最短距离;
然后对任意两个点
无向正权图中有一条边
设
强连通图的某点
先求
无向正权图的最短环?
遍历所有边,每轮循环时删除当前边,并且选取一端运行 Dijkstra 算法。如果另一端是可达的(不是
无向等权图中指定两点间最短路径数量?
BFS 使用两个队列。类似 copy collection,最终在队列 1 中找到与
这个方法的原理是利用 BFS 的性质:在每轮结束后队列中放的是相同长度的结点(分开放能确保下一轮的结点不会混入当前队列中)。
拓展:如果是有向/无向正权图,可以修改 Dijkstra 算法更新
dist[u] + l(u,v) == dist(v)时修改 bool 数组;
Chapter 5. Greedy Algorithms
5.1 Minimal Spanning Tree (MST)
对无向图,我们有引理 1:移除一个环上的边,不会改变这个图的连通性。
由引理 1,结合树的定义,我们可以得知:任何一个无向图,都有一个最小生成树,在保持原图连通性的同时边权和最小。
证明引理 2:对于一个树的数据结构,
1 个顶点、0 条边的图是树;
如果一个树有 k 个顶点、k - 1 条边;则对于一个 k+1 个顶点,在 k 个顶点的基础上添加一个无向边将新的顶点与树相连,则新的图也满足树的结构,并且拥有 k 条边;
对边数学归纳:
起始状态没有边,n 个顶点不相连,有 n 个连通部件。每次向其中加一条边,要求连接其中两个不同的连通部件,则全图的连通部件数减 1;
重复上述动作,总有一个时刻全图的连通部件数为 1,此时图满足树的定义,并且边为 n - 1 条;
证明引理 3(引理 2 的逆命题):一个无向连通图如果
如果满足
证明引理 4:一个无向图是一棵树 当且仅当 任意两结点间有一条唯一路径。分开 左推右 和 右推左:
Kruskal 算法求 MST:
初始只有顶点构成的森林,从小到大向顶点中加入边;如果不存在环则继续;如果存在环则移除这个边并尝试下一个边。最终直至加入
这本质上就是一个 greedy approach;
割定理:
如果边集
那么在连接
分类讨论 + 反证法证明 割定理:
设
假设
如果
Prim 算法求 MST:
从一个顶点组成的集合
正确性由割定理保证。
考虑新的上色算法:
先指定两条上色规则:
(破圈)如果
利用了树的定义,这步的转换肯定是正确的;
(闭圈)如果
利用了割定理,这步的转换也肯定是正确的;
在图上随便使用上述规则上色,直到所有边都着色为止。
最后所有的蓝色边就是这个图的 MST;
这个算法是正确的吗?我们已经知道了这两条规则是必要的,但是它能做到最后吗?
也就是说,如何证明这种上色方法能够一直做到全部上色完成而不产生冲突?
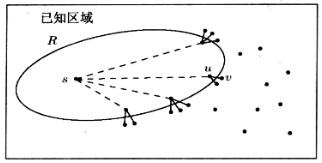
5.2 Set Cover(集合覆盖问题)
对一个分散的点集
这个问题等价于:
对一个点集
遗憾的是,这个问题暂时没有多项式时间算法(NP Hard)。不过我们考虑 Greedy Algorithm 作为近似算法。
如果我们用 Greedy Idea 思考:每次选能覆盖未被覆盖点最多的
理论上,我们能保证这种 Greedy Idea 最坏情况只会达到最优情况(optimal)的
证明:
设
是贪婪算法在第 次迭代后仍然没有覆盖的顶点数(易知 ),设最优的选取方案只需要 个集合; 由于剩下的顶点一定能被最优的
个集合覆盖,因此由鸽巢原理(抽屉原理),在这 个最优集合中,一定存在其中一个集合至少包含 个剩下的这些元素(反证;如果都包含少于 个元素,那么最后一定覆盖不完,这与 “最优集合能覆盖完所有顶点” 的前提矛盾)。 与此同时,贪心法会确保:
(因为贪心法会选出每步的最优解),所以数学上: 注意到
时, ,说明此时贪婪算法一定覆盖完全!因为是严格小于,所以贪婪算法取集合数量的最差不会比 的 倍更差。
5.3 贪婪算法何时失效:Coins Charging
如果有种货币面值:
Cashier's Algorithm 就是一个 Greedy Algorithm:每次选取
但是这种最优是因为特殊的面值组合。
如果换一种面值组合就不是最优(近似解),例如
甚至有时候贪婪算法没法得出解(任意坏):
嗯,贪婪算法之所以失效,就是因为局部最优解会逐渐偏离全局最优解。接下来我们将介绍一种能够解决这种问题的算法。
Chapter 6. 动态规划
我们在解决 DAGs 中最短路径的问题(线性化后逐结点解决)的时候,使用的就是动态规划。
动态规划的解决方案,就是解决子问题的途中记录下子问题的解,最后利用这些记录的解得出最终问题的解。
分治法和动态规划的区别?
动归:小问题和大问题大小差不多(两者都是包含关系);
动归:小问题不会 overrlap(很重要,充分利用了各个子问题的解);
6.1 最长子序列问题 I:最长递增子序列
给定一个数列
这个问题的思路可以是用图来解决:
每个元素就是一个结点;
插入一个有向边
这样所有的序列都可以转换为一个 DAG 图,那么原问题转换为求出这个 DAG 的最长路径。
对所有源顶点,
对所有顶点遍历
最终再次遍历
6.2 编辑距离
编辑器中需要有 spell checking,通常会检查 typos;而 typos 的修改建议就是借助了单词间的编辑距离。
编辑距离描述了一个单词最相近的另一个(改变次数最小,使得一个单词变成另一个单词);
我们使用一个二维表格(含有空白)来描述编辑距离:
其中
含义:只增大一方的长度(多考虑一个),则编辑距离就是在原本的基础上 + 1 个距离;如果同时增大双方的长度,则编辑距离取决于是否替换这个字符;
这被称为动态规划的 “状态转移方程”。
代码实现层面,看起来需要遍历全表,于是时间、空间复杂度
比较有意思的是,这里时间复杂度和空间复杂度都能优化:
在表
进一步使用分治(求最短路径)降低时间复杂度;
仅保留其中两列 / 两行来降低空间复杂度;
6.3 背包问题
6.3.1 01-背包问题
考虑一个问题题干:
假设有
求解在不超过容量限制的情况下,如何装入背包以获得最大价值。
在 01 背包的假设下,我们有前提:每个物品只有 1 件,只可以选择放或者不放。
这种做法比较简单,和之前我们讨论的编辑距离一样,都可以利用动态规划 “放一步看一步”。
定义状态表格
为什么是 “前
个”?因为动态规划需要子问题总是被包含在大的问题内;
很容易地得到状态转移方程:
注意,因为
也就是说,虽然我们不需要求
求解方法也很简单,就是填表,伪代码如下:
xxxxxxxxxxprocedure pack01(N, V, Costs, Values)# output: max value we can gain
F[0, 0...V] <- 0
for i <- 1 to N for v <- Costs[i] to V F[i, v] = max{ F[i - 1, v], F[i - 1, v - Costs[i]] + Values[i] }
return F[N][V];注意到这个
因为每轮
如果只保存
xxxxxxxxxxprocedure pack01(N, V, Costs, Values)# output: max value we can gain
F[0...V] <- 0
for i <- 1 to N for v <- V to Costs[i] F[v] = max{ F[v], F[v - Costs[i]] + Values[i] }
return F[V];问题变种:值得注意的是,这里并没有要求背包完全装满。如果要求背包必须恰好装满,应该怎么改?
答案是改变 F 初始化的方式就行。我们定
为什么?因为我们每次动态规划都是在找第
轮各个不同容量的背包的最大价值,相当于把每一轮都看作算法结束(因为是 “前 个物品”),因此这么设定最终会使得所有 “不能规约到剩余空间为 0” 的放置方法的价值都是 ;
此外,上述解法还有常数时间优化:在每轮
6.3.2 完全背包问题
题干仍然不变,但在完全背包的假设下,我们有前提:每个物品有无穷件,可以选择放
思路一:
思路和 01 背包相似,不过在遍历每种
即:
这下时间
注意到一个引理:
在完全背包的前提下,如果两个物品
在 01 背包中不能这么做,考虑一种情况:最后可能就只有
两个物品且背包不满。
这个引理可以完成常数时间的优化:
去除所有 cost 大于
找出所有 cost 相同但 value 最大的物品,作为这个 cost 下的唯一选择(不再考虑剩下的物品);
这个优化过程总体
最终我们需要落实解决并优化这个问题,可以把它规约到 01 背包问题上:
考虑把第
现在我们对拆分的过程优化一下:
把第
也就是说,把第
这是一种算法。时间复杂度
思路二:
还有一种思路:重写状态转移方程。注意到一个物品可以选不止一次,因此新的状态转移方程是:
注意到,这时我们考虑选择第
而且我们发现这个时候由于不依赖
时间复杂度
6.3.3 多重背包问题
题干仍然不变,但在完全背包的假设下,我们有前提:每个物品有有穷件,可以选择放
其实就是完全背包的特例,只不过相当于限制了
这个时候我们只有一种思路:
在遍历的循环内层加一层遍历
然后优化方法同 “完全背包”,使用二进制表示法来优化。时间复杂度
xxxxxxxxxxprocedure MultiplePack(F, C, W, M):
# 对每个物品而言,存在个数 M 总是比容量可观,# 因此 M 不是限制,直接转换成完全背包if C * M >= V CompletePack(F, C, W) return# 将 M[i] 个物品拆成系数 1, 2, 2^2, ..., M[i] - 2^k + 1 的 k 个不同的物品# 这 k 个物品作为分别作为 系数*价值、系数*cost 的 01-物品 来计算 01 背包问题k <- 1while k < M Pack01(k * C, k * W) M <- M − k k <- 2kPack01(C * M, W * M)我们还可以结合在完全背包中介绍过的常数时间优化,来应对这个问题。
可惜的是,在这种情况下没有
拓展一下:
如果多重背包问题需要恰好填满背包,并且别管最大价值了,那么这个时候就有
这个时候
xxxxxxxxxxprocedure multiKnapsackFeasible(N, V, Costs):# output: F[N][0...V]
F[0, 1...V] <- -1 # 不放东西是解决不了问题的F[0, 0] <- 0 # 除非容量是 0
for i <- 1 to N # 对第 i 个物品 # 讨论各种背包容量 for j <- 0 to V # 如果当前容量下,用前 i - 1 件物品不能恰好填满,则前 i 件也彻底没救 # 如果前 i - 1 件可以,先把所有第 i 件物品全部放进去(可能溢出,后面判断) if F[i - 1][j] >= 0 F[i][j] = M[i] else F[i][j] = -1 # 前 i - 1 件物品放完后,剩下空间足够放第 i 件物品的话,就用状态转移看看第 i 件物品放几个 for j <- 0 to V - Costs[i] if F[i][j] > 0 F[i][j + Costs[i]] <- max{ F[i][j + Costs[i]], F[i][j] - 1 }
6.3.4 问题变种:Optimal Solution for Coins Charging
现在我们再来看上一章用贪婪算法解决不了的 “硬币找零” 问题,发现其实它就是另一种形式的背包问题:
硬币就是这里的 “物品”;
要凑的总面值就是背包的容量;
硬币面值就是 cost;
硬币的 value 看作全部相等(不妨设为 1,这样
现在硬币找零,就是一个 “要求将物品恰好填满背包、并且价值最小(不是最大)” 的完全背包问题。
直接写出状态转移方程:
好,问题解决。我们只需要注意:
同理可以只用一维列表解决这个问题;
对于恰好填满背包的,记得初始情况
具体选取的方案可以在每层循环决定时记录在额外的数组中(如果需要的话),不影响时间和空间复杂度。
如果每种硬币数量有限,那么就是需要恰好填满的“最少”多重背包问题。这里不再赘述。
6.4 最长子序列问题 II
6.4.1 最长公共子序列
对于可比较序列
这个问题其实就是之前编辑距离的特例。我们同样引入 “匹配距离” 的说法:
定义
当一个为空序列,另一个有元素时,公共子序列长就是 0(
状态转移方程:
常数优化方法是,如果
最后最优解就在
6.4.2 最长公共子串
对于可比较序列
就是 “最长公共子序列” 的特殊情况:
在状态转移方程中,如果
并且最长公共子串的最优解在表的任意位置,需要遍历得到。
当然,上述只是最基础的方案,你能在网上/论文里找到更快的算法,不过它们大多数都是基于这个算法改进得到的。
6.4.3 Quiz: 最大连续子序列和
对于一个整数集
(复习)考虑使用分治法的时间复杂度是多少?
一分为二,求:左边、右边的最长子序列;最后合起来求跨越中间的最长子序列(
如何尽快得到最大的连续子序列和?
最快使用动态规划。它能达到理论下界
定义一个一维列表
这样有状态转移方程:
思考:为什么讨论 “以
因为这样讨论可以明确状态转移方程是向子序列的后面追加,或者根本不在当前讨论范围内。如果以
DP 填表 General Method:
DP 填表,决定表格的维数和含义;
出口是什么?(最容易的 entries);
填表的顺序是将大问题拆解为小问题的思路;
最优解在表的什么部分;
6.5 3-Partition Problem
三分问题(3-Partition problem):给定整数集合
定义一个四维数组
因此有递推式:
出口
答案是
6.6 跳石子
在一条河上有一座独木桥,长度为 L,上面分布着一些石子,为了简单起见,我们假设桥为 0-L 的一段线段,而石子都分布在整数坐标上,也就是有一个函数 stone(x),表示在坐标 x 上是否有石子,比如 stone(0)= 1 表示在桥头有一个石子,stone(2) = 0 表示在坐标为 2的位置没有石子。 现在有一个小朋友站在桥头的位置想要过桥(站在桥尾或者跨过桥尾均为过了桥),但他不想踩到石子,他每跨出一步的步长是 [S,T] 区间中的任何整数(包括 S 和 T)。设计算法求小朋友要过河,必须踩到的最少的石子数。
设一维表
显然,时间复杂度
6.7 Shortest Reliable Path (Lite) & Revisit Bellman-Ford Algorithm
在网络拓扑图中,如果用边长表示传输时延,并且需要考虑到每一跳的丢包问题,因此需要尽可能避免边数过大。
定义问题:给定图
以
出口
答案是
这里可以用动态规划的思想理解 Bellman-Ford Algorithm。对单源填一个表的时间
那么如果想知道每两个顶点间的最短路径,用上述算法的时间
6.8 Revisit Shortest Paths Problem: Floyd-Warshall Algorithm
对图
出口:
状态转移式在 “从
到 的经过前 个结点的最短路” 的前提下,分为两类情况:
这个从
到 的最短路不经过 ,那么一定经过前 个顶点,最短路的数据保存在前 的表格中; 这个从 𝑖 到 𝑗 的最短路经过
,那么一定可以从 拆成两条路径,一个以 为起点,另一个以 为终点;
那么从
6.9 Traveling Salesman Problem (TSP)
给定一个无向连通图
一般讨论完全图。因为如果两个城市间不存在路径,则添加一条远大于其余边权的边,这样不影响计算最优回路;
简单来说,如何找无向连通图
中最短的 H 回路。
Brute-Force 算法:遍历从
使用动态规划:为每个结点标记序列
这样对
含义解释:在子问题对应的点集
中,从 1 开始到 结束的最短初级回路,一定可以转换为求从 1 到 前一点 的最短初级回路再到 的情况。这个 “子路径最短性” 我们在 Dijkstra Algorithm 证明时已经阐述过了。
由于子集
出口
可惜的是 TSP 问题即便使用动态规划也无法在多项式时间内解决。它是个 NP Complete 问题(因为等价于求子集问题)。
6.10 Independent Sets in Trees
独立集(Independent Sets)问题是指,对于一个图
这个问题也是一个 NP Complete 问题(也和集合的子集数量有关)。
但是如果这个图
我们定义
解释一下,树中的两个结点不相连的情况很多,但是如果我们从共同的根结点开始看,那么就只需要讨论两类情况:
树根与孙子结点,它们俩一定可以在一个独立集中(+1),可以继续考虑以孙子结点为根的子树的独立集数量;
树根与儿子结点,它们俩一定不能在一个独立集中,因此直接讨论以儿子结点为根的子树独立集数量;
最终此法时间复杂度
Chapter 7. Linear Programming
7.1 Definitions
定义:给定一组变量,要求它们的一组取值使得:
满足约束这组变量的等式和不等式;
最大化或最小化给定的线性目标函数;
举个例子:
对于两个变量:
线性不等式约束组成二维空间的半平面;
线性等式约束组成二维空间的一条直线;
所有线性约束可能形成一个凸多边形,这是可行空间(feasible space);如果不能形成可行空间,称约束为 infeasible;
线性目标函数
则由凸多边形的性质,线性目标函数的最值
可行空间是 infeasible 的;
可行空间过大,我们称这是 unbounded 的;
最值
最值
对于三个变量:
线性不等式约束组成三维空间的半空间;
线性等式约束组成三维空间的一条直线;
所有线性约束可能形成一个凸多面体;
于是更一般的形式上,我们可以定义线性规划的规范形式(Canonical Form):
松弛型(Slack Form):
在 Computer Algebra System 中非常有用。
所有线性规划问题都能通过以下方法转换为规范型或松弛型:
如果讨论 minimize
一个不等式
例如
一个等式
所有非约束变量可以被转换为
例如:
可以被转换为:
解决上述线性规划问题的算法之一就是 simplex(单纯形法),它描述:
从可行空间代表的凸多边形的任意一个顶点出发,按任意方向遍历凸多边形的相邻顶点,找到使 objective function 的局部最优值(没有任何相邻结点能使得 objective function 的取值更优),即为线性规划的解。
但实践上有几个问题:
为什么局部最优解是全局最优解?
Answer: By simple geometry. Since all the vertex’s neighbors lie below the line, the rest of the feasible polygon must also lie below this line.
如何得到可行空间的顶点?
如何得到顶点的相邻顶点?如果退化造成死循环又该怎么办?
我们将在讨论完 “对偶问题” 的概念后再回来解决。
另一个算法是椭球法,由苏联科学家发现。我们这里不作详细描述,只需要知道它是多项式时间复杂度的算法即可。
还有一个算法是内点法,也是时间复杂度。
7.3 Integer Linear Programming
整数规划并不是说直接可以通过一般线性规划直接得到的,因为解可能是小数,仅仅做舍入运算是不一定能得到最优解的(舍入可能造成偏离目标,但有可能其他原先不是最优的点在舍入后最优了),可能是近似解。
整数规划就是一种 NP Problem,除非使用普通线性规划的解恰好是整数,否则不能很快地求出最优解。
常见方法有剪枝、动归等等。我们后面讨论。
7.4 Dual Program
同样考虑这个问题:
如何验证这个线性规划的最优解是
可以通过线性约束的线性叠加,得到关于目标函数的最紧的约束(
因此我们进行配凑:
我们希望
也就是说,原问题转换为了:
我们总结一下转换的方法:
原问题
原问题目标函数中的常数直接挪到对偶问题的目标函数中;
原问题 和对偶问题的
原问题变量 和 对偶问题的约束条件互换:
原问题变量
原问题变量
原问题变量无限制,对偶问题约束条件
原问题约束条件 和 对偶问题的变量互换:
原问题约束条件
原问题约束条件
原问题约束条件
另外,这种对偶问题还有 Complementary Slackness(互补松弛)来描述这种 “相互为最紧约束” 的性质:
对线性规划问题
如果
如果
如果
如果
以上面的问题以及它的对偶问题为例,我们发现原问题解
7.4 Application: Shortest Path
给定一个有向正权图
我们可以用线性规划表示这个问题!
这个线性规划实际上是在描述 Dijkstra Algorithm。
假设图上有一些橡皮筋,现在
注意到如果
我们回想,Dijkstra Alogrithm 的步骤是不断更新
的 的值,也就是让期望值和真实值接近;而这里相反,则是讨论真实值( 是 真实最短路径长)的约束关系。
这恰好对应该约束条件紧绷(取等)的状态,我们可以从数学角度证明这点。
再看另一个角度:
设
我们可以将
其中
上面的线性规划可以理解为,在
那么我们能将
更进一步地,
我们注意到新问题的对偶问题:
注意借助对偶变量的个数来列式。对偶变量
共有原问题约束变量的个数( 个);
这个对偶问题是有含义的。注意到
7.5 Simplex Algorithm
7.5.1 算法内容
算法内容:我们需要可行域中的任意一个顶点
我们定义单纯形:
单纯形的顶点:对于所有约束条件(不等式)的子集
感性理解:每个单纯形的顶点都是一系列超平面的交点(每个顶点可由
两个顶点是相邻的,当且仅当它们两有
对每一次迭代,Simplex 需要:
check 当前结点间是不是 optimal 的点(要比较所有邻居,不好做);
确定个下一步需要到达的点(用不等式找顶点,不好找);
我们知道,如果当前顶点是原点,上面两个操作会非常简单。因此我们可以每轮迭代都进行一次坐标变换,把下一次要处理的点变成原点。
为什么顶点是原点就简单?
首先 task 1 判断是否为最优点会比较简单:
当原点是顶点,线性规划必定满足(
因为原点恰好满足
共 个不等式的取等(紧绷)且在可行域内,因此原点是顶点。
假设原点是最优解,即
证明:因为一旦存在一个
,那么一定有更大的 能取到更优的值;
其次 task 2 判断下一个需要到达的点也会比较简单:
如果此时原点不是最优点,那么对于这个
此时
那么如何在这个点的基础上继续重复呢?我们需要变换坐标系,让上面的更优点为原点,手工解法是,让
7.5.2 Corner Cases
考虑新的情况,如果原点不是顶点怎么办?这个时候说明变量不全是大于等于 0 的(原点可能不在可行域内)。我们只要转为规范型就行了!
这里我们换一种思路,转成松弛型。并且确保所有等式约束条件右边常量都是正数(不是就乘以
然后,我们构造一个新的线性规划:
创建
将
将目标函数换成
我们注意到,这个新的线性规划有很好的性质,
如果
再考虑一个可能会使单纯形法失效的情况:退化。也就是说一个顶点可能由多个超平面相交得到,多于确定一个点所需的个数。
以 3 个变量的退化的线性规划为例,可能一个顶点会满足 4 个不等式,这会导致无论选哪三个约束条件并松弛另外一个,都会超出可行域(也就是当前顶点的所有邻居和这个点一样好),进而造成死循环。
破局的方法是,向约束条件的常数添加一个极小的扰动(加或减 0.00001),这不会对最优解的获得造成影响,但能够区分各个约束条件,以跳出这个怪圈。
另外,单纯形法能应对 unbounded 吗?可以,只要出现一种情况:在松弛一个不等式时,无论如何都碰不到下一个不等式取等了。这个应对方法是设定一个最大/最小阈值,松弛到这个值还找不到就算 unbounded;
7.5.3 运行时间
对于一个规范型线性规划,假设它有
我们知道,一共有
每轮单纯形算法总是从
每轮进行坐标变换的复杂度最多
同时,单纯形所有顶点的最多个数为
因此单纯形算法上界
不过线性规划是多项式时间内能解决的问题,因为椭球法、内点法是多项式时间复杂度的。
但好笑的是,单纯形算法虽然是指数级算法,但是实践中要比椭球法、内点法在大部分情况下更快。
研究人员对这个问题使用了 Smoothed Analysis,获得了2008 年的哥德尔奖。研究证明了单纯形法只有在每一轮都取到一个特定的特殊的顶点时才会 fallback 到指数时间,否则有一点扰动就极大概率是多项式时间能完成的。
7.6 最大流与最小割
最大流问题:对于一个有向图,边权为该边的流量限阈。其中图中除了源点、汇点外,流体无法存储、无法产生。
在不超过每条边的容量前提下,我们希望尽可能多地从源点
我们设每条边权(容量)
流入和流出的关系:
目标流量(离开源点
如果我们从汇点到源点连一条有向边,这样取消了
此时让
注意到我们可以更改约束条件都为
目标流量(进入源点
在线性规划的思路中,我们怎么做?
先确定原点(
于是,在每次迭代中,找到的一条路径(不小于前一条路径的流量,且这条路径后一个边不能小于前一条边),因此该路径的每一条边都满足下面两种情况之一:
其反向边
对第一种情况,边
对第二种情况,最多增加的流量就是
因此我们可以定义一个新的图
这样,我们模仿单纯形法,获得计算最大流的算法:
从全空流开始,计算剩余网络
问题:给定一个有向图(含多个源点和汇点),判断它是否是流通的(circulate);
创建一个源点
应用:二部图匹配。
创建一个源点
则原问题等价于 “在新的图中是否有最大流的流量等于最终配对数”。
注:最大流问题的整数性。
如果所有边的容量为整数,则算法得到最大流规模也是整数。因为算法每次迭代都增加的是一个整数值的流量。
如果边的容量不是整数(例如实数),那么最大流的很多算法没法使用,例如上面的剩余网络算法可能无法终止。
Chapter 8. NP Problems
本章几乎全部是概念。
首先,问题和算法是两个概念。
有效问题 和 难问题:有没有一种问题,存在指数级别的 search space,且无论如何都无法找到多项式时间的算法?
例如最小生成树(Kruskal/Prim)算法能在指数级 search space 中使用接近线性时间的复杂度完成任务。这就是一个简单问题(P);
再例如可满足问题(SAT)。如果每个 clause 的 word 数量都是 2(称为 2-SAT 问题),那么可以将
那么如果是 3-SAT 问题呢?(人们发现 N-SAT,
SAT 问题就是典型的 search problem。我们现在定义两个概念:
实例(instance)
解(solution)
而一个 search problem 必然满足一个性质:给定一个
一个 search problem 的
我们再来看看旅行商问题(TSP):这个问题我们换一种表述方式。给定
理论上,我们认为 optimization problem 和 search problem 的相互转换不会改变时间复杂度,因为:
优化问题转判定问题:找到最优问题的解,判断是否满足判定问题条件;
判断问题转优化问题:通过二分法试探问题的最优解;
又因为判定问题 和 搜索问题可以通过图灵机进行等价,因此:优化问题、判定问题、搜索问题可以相互转换(一个问题就有 3 个版本)。
通常,判定问题用作判断问题的复杂度(参数复杂性);优化问题版本通常用来求解近似算法;
最小割问题(移除最少边使得图不连通),可以通过执行
而平衡割问题(balanced-cut,每个割集内结点数不少于
ZOE:一个线性方程组系数只能是 0/1,解的取值也只能是 0/1;它和整数规划一样,不存在多项式时间算法。
因此 3 维匹配问题可以转化为 ZOE 问题(一个匹配 triple 作为一个变量),所以 3D Matching 是不存在多项式时间算法的。
独立集问题(最大顶点子集互不相连)、顶点覆盖问题(所有边至少有一个顶点在当前顶点子集中)、团问题(最大顶点子集间两两有边)三者实际相互等价。
独立集问题考虑图
考虑图
(顶点覆盖是集合覆盖的子集?)
子集和问题(取一个给定整数集的子集,使这个集合元素和为指定值),可以转为整数规划问题
NP:所有种类的 search problems。多项式时间内可验证的问题(判断标准);
co-NP:NP 问题的补问题。一般认为 co-NP 和 NP 的交集包含 P;
P:可以多项式时间内可以求得解的 search problems(
P 问题有一条性质:关于补问题是封闭的(
P = co-P);
为什么说只要解决一个 NP 问题,就能解决所有 NP 问题(Solve one and solve all)?
因为可以规约(reduction):将问题
解决问题:将未知问题规约到已知问题(已知问题有一个算法,将未知问题用这个算法来解);
证明问题:将已知问题规约到未知问题(证明未知问题难以已知问题);
评估问题:将未知问题规约到已知问题(问题规约到更难的问题看看参照,不作为科学证明);
NPH:NP Hard 问题,可能没法在多项式时间内验证的问题。
NPC:NP 完全问题,其他所有 NP 问题都能规约到它(因此 NPC 不简单于 NP)。
证明:如果 NP != co-NP,则 P != NP;
如何将 H 路径问题向 H 回路(顶点和边不重复的)规约?
f: 在原图
g: 如果有 H 回路,则删除这两条边,记为原问题的解(H 道路);如果没有 H 回路,则原问题无解;

如何将 3-SAT 问题规约到独立集问题?
考虑任意一个 3-SAT:
将每个子句中的每个文字连接一个无向边(在 3-SAT 问题中会形成多个三角形)、将每个文字与其他所有反向出现(
这时形成一个图
我们知道
如何将 SAT 问题规约到 3-SAT 问题?
注意任意 SAT 问题的任意子句
解释:除了第一个、最后一个子句有两个
,以及一个 / 以外,中间的所有子句都是由前一个子句正出现的 取反,以及下一个子句反出现 对应的正出现;
这两个子句不完全等价,但有个性质:它们同可满足性;
先证明
corner case I:
corner case II:
common case:
再证明
进一步,3-SAT 即便再简化都是难问题!例如,我们让每个变量最多出现 3 次、每个文字最多出现 2 次;
如何将 H 回路问题规约到 TSP 问题(H 回路的权值和最小)?
考虑两个问题的不同(以便构造 input f):
多了权值;
并且 TSP 一般考虑完全图的情况;
f:将 H 回路补上边使得它称为一个完全图(完全图一定存在 H 回路),但是旧的边权设置为 1,新补的边设置大于 1;
对新图执行一次 TSP 算法(假设有),如果边权和能小于等于预算
如何应对 NP 问题?
梯度下降
vertex cover:从
可能获得的局部最优离整体最优很远:星形图如果意外删除中心结点?二部图删除了结点少的一边?
TSP:交换 2 个边的匹配关系(2-change neighborhood,交换方法
graph partition:
Metropolis Algorithm:固定温度的退火算法;
内容:像之前一样,检查邻居并更新。但是如果邻居不是更优,则有
优点:每次 iteration 都有概率到全局最优(不会只看到局部最优);
缺点:算法难以结束(不可能跳出局部最优的时候仍然“不愿意”收敛);
Simulated Annealing:模拟退火算法;
加入 Cooling Schedule:对指定迭代轮次有不同的温度
在 Metropolis Algorithm 的基础上保证算法能快速结束;
Hopfield Netural Network
给定一个无向图,图上每个顶点要么 +1,要么 -1(两种状态,记顶点状态
我们定义 configuration:顶点状态的一个指派;
定义一个 good edge:该边如果负权,则顶点状态相同,正权则顶点状态相反;
也就是希望两个顶点边是负值顶点状态相同,边是正值顶点状态不同;
定义一个 satisfied node:该点连着的 good edges 权重高于 bad edges 的权重。用数学表示:
定义一个 stable configuration:一个对顶点状态的指派,使得所有顶点都是 satisfied nodes;
我们对任意一个连通的无向图,希望找到一个 stable configuration;
这样我们发现,只要把 unsatisfied nodes 的状态 flip 后,至少当前的顶点会变成 satisfied node!
我们让这样的 flip 变换的 configuration 为一个邻居,就有 local search: